3.3. Классификация смо и их основные характеристики

Рассматриваются системы обслуживания, в которых имеется как входной поток, так и поток обслуженных заявок и способные одновременно обслуживать c клиентов, т. е. имеющие c параллельных обслуживающих устройств. При этом все обслуживающие приборы с точки зрения быстродействия предполагаются эквивалентными.

Обозначения, которые представляются наиболее подходящими для СМО с параллельно «включёнными» приборами, давно уже унифицированы и имеют следующую структуру:

(a /b /c) : (d /e /f), (3.3.1)

где символы a, b, c, d, e и f сопоставляются конкретным наиболее существенным элементам модельного представления процессов массового обслуживания и интерпретируются следующим образом:

a — распределение моментов поступлений заявок на обслуживание;

b — распределение времени обслуживания (или выбытий обслуженных кли ентов);

c — число параллельно функционирующих обслуживающих устройств (c = 1, 2, …, ∞);

d — дисциплина очереди (ПЕРППО, ПОСППО, СОЗ);

e — максимальное число допускаемых в систему требований (число требова- ний + число требований, принятых на обслуживание);

f — ёмкость источника, генерирующего заявки на обслуживание.

Для конкретизации a и b приняты такие стандартные обозначения:

M — пуассоновское (или марковское) распределение моментов поступ ления заявок на обслуживание или выбытий из системы обслу женных клиентов / (что аналогично) экспоненциальное распреде ление интервалов времени между моментами последовательных поступлений или продолжительностей обслуживания клиентов;

D — фиксированный (детерминированный) интервал времени между момен тами последовательностей поступлений в систему заявок на обслужи вание или детерминированная (фиксированная) продолжительность об служивания;

E_k — распределение Эрланга или гамма-распределение интервалов времени между моментами последовательных поступлений требований в об служивающую систему или продолжительностей обслуживания (k – параметр распределения)

GI — распределение произвольного вида моментов поступления в систему заявок на обслуживание (или интервалов времени между последова тельными поступлениями требований);

G — распределение произвольного вида моментов выбытия из системы об служенных клиентов (или продолжительность обслуживания).

Рассмотрим, например, структуру (M / D / 10) : (GD / n / ∞). Здесь речь идёт СМО с пуассоновским входным потоком, фиксированным временем обслуживания и десятью идентичными параллельными каналами обслуживания. Дисциплина очереди не регламентирована (то есть при моделировании данной СМО задаётся произвольно). Однако, независимо от того, сколько требований поступает на вход обслуживающей системы, данная система (очередь + обслуживаемые клиенты) не может вместить более n требований, т. е. заявки, не попавшие в блок ожидания, покидают систему. Наконец, источник, порождающий заявки на обслуживание, имеет неограниченную ёмкость.

Стандартные обозначения, приведённые выше, впервые были введены Д. Г. Кедаллом (1953 г.) в форме a /b /c – т. н. обозначения Кендалла. Позднее А. М. Ли (1966 г.) добавил к обозначениям Кендалла символы d и e, а в 1982 г. Х. А. Таха счёл целесообразным расширить группу символов, добавив символ f.

Конечная цель анализа систем и процессов массового обслуживания заключается в разработке критериев (или показателей) эффективности функционирования СМО. Так как процесс массового обслуживания протекает во времени, важно заранее определиться, какой режим функционирующей системы нас интересует – неустановившийся (переходной) или стационарный. В СМО, с одной стороны, происходит поступление заявок на обслуживание, а с другой – обслуженные клиенты покидают систему. Случайные процессы, описывающие два этих потока относятся к так называемым процессам рождения (размножения) – вход, и гибели (вымирания) – выход. Среди и тех и других есть очень разные процессы, в том числе и нестационарные и неординарные. Если не ограничивать входящие/выходящие потоки в СМО стационарными потоками (или, хотя бы, со стационарными приращениями – например, винеровский процесс), то трудно ожидать со временем установившегося режима функционирования СМО. При выполнении указанных требований, по истечении достаточно большого интервала времени достигается стационарный режим функционирования СМО.

Замечание 3.2. Для СМО с постоянной интенсивностью поступления заявок λ и постоянной интенсивностью выходного потока μ мы вправе ожидать отсутствия стационарного режима и бесконечного возрастания очереди, если μ < λ. Но хорошей математической моделью такой системы будет процесс размножения и гибели с теми, же постоянными параметрами: λ – интенсивность размножения, μ – интенсивность смертности. При этом можно показать что по крайней мере бесконечного возрастания очереди не стоит ожидать, и более того, при μ = λ получаем p₀(t) = 1, т. е. система «вымирает» (нет заявок).

При выполнении условий стационарности представляют интерес следующие операционные характеристики СМО:

p_n – вероятность того, что в системе находится n клиентов (заявок на обслу- живание);

L_S – среднее число находящихся в системе клиентов (заявок на обслужива ние);

L_q – среднее число клиентов в очереди на обслуживание;

W_S – средняя продолжительность пребывания клиента (заявки на обслужива- ние) в системе;

W_q – средняя продолжительность пребывания клиента (заявки на обслужива ние) в очереди.

По определению

L_S = ;L_q =. (3.3.2)

Между L_S и W_S (как и между L_q и W_q) существует строгая взаимосвязь, так что, зная числовое значение одной из этих величин, можно легко найти значение другой величины. В частности, если частота поступлений в систему заявок на обслуживание равняется λ, то имеем

L_S = λW_S; L_q = λW_q. (3.3.3)

Приведённые выше соотношения справедливы и при гораздо менее жёстких предположениях, не налагающих никаких специальных ограничений ни на распределение моментов последовательных поступлений требований, ни на распределение продолжительностей обслуживания. Однако в случаях, когда интенсивность входящего потока заявок равна λ, но часть заявок теряется (например, из-за ограниченности очереди), соотношения (3.3.3) следует поправить, введя вместо λ величину λ_эфф = βλ, 0 < β < 1. Если обслуживание заявок подчинено экспоненциальному закону с параметром μ, то средняя продолжительность обслуживания равна 1/ μ, а средняя продолжительность пребывания заявки в системе

W_S = W_q + 1/ μ. (3.3.4)

Умножив это равенство на λ получим

L_S = L_q + λ / μ. (3.3.5)

Это соотношение остаётся справедливым и в том случае, когда заменяется λ на λ_эфф, поэтому

λ_эфф = μ(L_S – L_q). (3.3.6)

Отметим, что в большинстве случаев при вычислении основной характеристики всех моделей СМО p_n особых трудностей не встречается. Численная же оценка распределений продолжительностей ожиданий может вызвать значительные затруднения. Таким образом, в большинстве случаев удобнее вычислять W_S и W_q через L_S и L_q .

Ниже приводятся основные характеристики некоторых типичных моделей СМО (в стационарном режиме). Так как вывод соотношений для p_n совершенно не зависит от дисциплины очереди в данной системе, то во многих случаях будем считать её произвольной, что маркируется в схеме Кендалла символами GD. В тех случаях, когда дисциплина очереди будет конкретизироваться, будет приводиться формулы распределения продолжительностей ожидание, вывод которых невозможен без учёта дисциплины очереди.

Модель (M/M/1):(GD/∞/∞).

Входной и выходной процессы - пуассоновские с параметрами λ и μ соответственно. Для этой системы существует стационарный режим , т. е. при неограниченном возрастании времени (t → ∞) вероятность того, что к моменту t в системе будет n заявок p_n(t) сходится к постоянной величине p_n.

Рассмотрим кратко алгоритм получения этой величины. Для достаточно малого h > 0 справедливы соотношения (а при h → 0, что производится в дальнейшем, это точные равенства): вероятность непоступления заявок в интервале времени h – P{+0, h} = e ^{– λh} ≈ 1 – λh; вероятность поступлеия заявки P{+1, h} = 1 – e ^{– λh} ≈ λh; вероятности за это время покинуть ситему нулю и одной заявке, соответственно равны P{–0, h} = e ^{– μh} ≈ 1 – μh; P{–1, h} = 1 – – e ^–μh ≈ μh. Событие, состоящее в том, что в системе в интервале времени

[t, t+h] находилось ровно n заявок, складывается из следующих несовместных событий: к моменту t в системе находится ровно n заявок и за промежуток h новых не поступает и ни одна заявка систему не покидает; либо к моменту t в системе находится n – 1 заявка и за промежуток h поступает ровно одна, но ни одна заявка систему не покидает; либо к моменту t в системе находится n + 1 заявка и за промежуток h новых не поступает, но одна заявка систему покидает; или к моменту t в системе находится ровно n заявок и за промежуток h поступает одна заявка и одна заявка систему покидает. Так как вероятность последнего события ~ h², поэтому для малых h её можно не учитывать. Сказанное позволяет записать систему уравнений в конечных разностях

p_n(t+ h) ≈ p_n(t)(1– λh)(1– μh) + p_{n – 1}(t)(λh)(1– μh) + p_{n + 1}(t)(1– λh)(μh), n  1;

p₀(t+ h) ≈ p₀(t)(1– λh)·1 + p₁(t)(1– λh)(μh), n = 0;

в последнем соотношении учтено то, что вероятность того,что в интервале h не произойдёт ни одного выбытия, равна единице.

Перенеся (после раскрытия скобок и отбрасывания всех слагаемых имеющих множитель h в степенях выше первой) p_n налево и разделив равенства на h, переходим к пределу при h → 0, получаем систему дифференциальных уравнений

p_n' (t) = λ p_{n – 1}(t) + μ p_{n + 1}(t) – (λ + μ) p_n(t) , n  1;

p₀' (t) = – λ p₀(t) + μ p₁(t), n = 0.

Решение этой системы дифференциально-разностных уравнений позволяет в принципе найти все p_n(t), которые описывают стохастический процесс, в общем случае нестационарный. Можно доказать, что при t → ∞, по крайней мере для λ < μ (см. замечание 3.2), существует стационарный режим p_n' (t) = 0,

p_n(t) → p_n , n= 0,1,…. Cистема дифференциальных уравнений принимает вид

– λ p₀ + μ p₁ = 0, n = 0,

λ p_{n – 1} + μ p_{n + 1} – (λ + μ) p_n = 0, n  1. (3.3.7)

Решая эту систему имеем:

p_n = (1 – ρ) ρⁿ, n = 0, 1, 2, …; ρ = λ / μ < 1. (3.3.8)

Тогда среднее число находящихся в системе клиентов (заявок) и средняя продолжительность пребывания клиента (заявки) в системе

L_S = M{n} = (1 – ρ) ρ; W_S = L_S / λ = 1/ [μ(1 – ρ)], (3.3.9)

среднее число и средняя продолжительность пребывания клиентов в очереди на обслуживание

L_q = L_S – λ / μ = (1 – ρ) ρ²; W_q = L_q / λ = ρ / [μ(1 – ρ)]. (3.3.10)

Распределение продолжительностей ожидания τ при дисциплине ПЕРППО (плотность вероятностей)

w(τ) = μ(1 – ρ)∙e ^{– μ(1 – ρ)τ} , τ > 0, (3.3.11)

т. е. случайная величина τ экспоненциальное распределение параметром

μ(1 – ρ), т. е математическое ожидание Mτ = W_S .

Модель (M/M/1):(GD/n/∞).

Отличие от предыдущей задачи лишь в том, что в системе одновременно может находиться не более n заявок (вместе с вновь поступившей). То есть часть поступающих заявок получает отказ в обслуживание и теряется для системы. Составляя и решая систему уравнений в конечных разностях для p_n этой системы, получаем (по прежнему ρ = λ / μ)

p_m = m = 0, 1, 2, …, n. (3.3.12)

С учётом приведённого соотношения, выражение для среднего числа находящихся в системе заявок принимает вид

L_S = (3.3.13)

Выражения для L_q , W_S и W_q можно получить из формулы (3.3.13), если предварительно вывести формулу для λ_эфф. Поскольку вероятность того, что заявка не может присоединиться к очереди, равняется p_n , доля заявок, которым разрешено войти в блок ожидания, равняется P{ m < n} = 1 – p_n . Отсюда следует, что

λ_эфф = λ(1 – p_n), (3.3.14)

L_q = L_S – λ_эфф /μ = L_S – λ(1 – p_n)/μ; (3.3.15)

W_q = L_q / λ_эфф = L_q / [λ(1 – p_n)]; (3.3.16)

W_S = W_q +1/ μ = L_S / [λ(1 – p_n)]. (3.3.17)

Пуассоновский характер выходного потока говорит о том, что время обслуживания одной заявки подчинено показательному (экспоненциальному) закону со средним 1/ μ. В этом случае величина, численно равная ρ , а по смыслу приведённая плотность заявок (среднее число заявое приходящееся на среднее время обслуживания одной заявки):

α ≡ ρ = λ / μ = λm_t

Модель (M/G/1):(GD/∞/∞).

Входной поток – пуассоновский с интенсивностью λ; продолжительности обслуживания независимы в совокупности и одинаково распределены по произвольному закону (со средним значением m_t и дисперсией σ_t²); обслуживающее устройство – единственное; выполняются условия стационарности при ρ = λm_t < 1.

Так как выходной процесс имеет произвольный характер, процедура составления конечноразностных уравнений для анализа функционирования данной СМО усложняется и требует привлечения вложенных цепей Маркова.

Среднее число находящихся в системе заявок L_S определяется формулой Полачека – Хинчина, имеющей для этой модели СМО вид:

L_S = λm_t + (3.3.18)

Зная L_S легко получить и другие характеристики: среднее число заявок в очереди

L_q = L_S – λm_t = (3.3.19)

Среднее время пребывания заявки в очереди

W_q = L_q / λ =; (3.3.20)

и среднее время пребывания заявки в системе

W_S = L_S / λ = m_t + 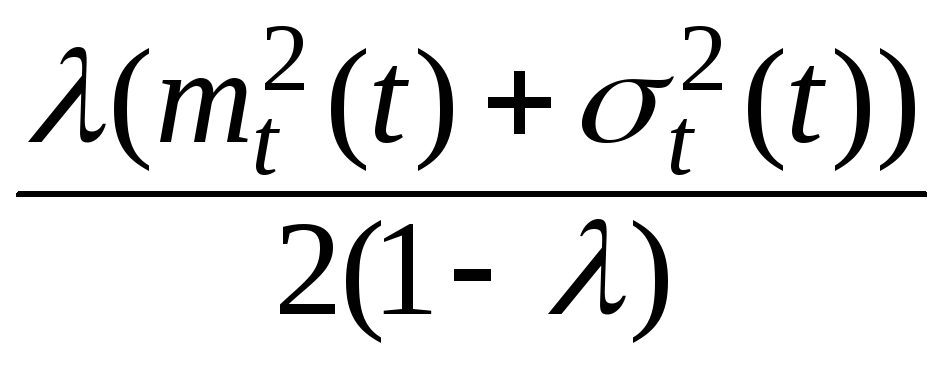. (3.3.21)

Зметим, что средняя скорость обслуживания μ = 1/ m_t .

Замечание 3.3. В общем случае формулами Полачека – Хинчина для указанного типа СМО называют соотношения

(3.3.22)

справедливые при λβ₁ < 1, где ω(s) = – преобразование Лапласа функции распределения времени ожидания обслуживания; P(z) = – производящая функция (дискретное преобразование Лапласа распределения вероятностей числа поступивших в систему заявок); λ – интенсивность входящего потока; β₁ – математическое ожидание времени обслуживания (с функцией распределения B(x)); β(s) = – преобразование Лапласа этой функции распределения.

Модель (M/M/c):(GD/∞/∞).

Входной и выходной пртоки – пуассоновские. Интенсивность входного потока – λ. Средняя продолжительность обслуживания одной заявки равняется 1/ μ. Так как на ёмкость очереди не накладывается ограничений, то число n поступивших в систему заявок может быть и меньше c и больше c. Однако интенсивность выходного потока равна nμ при n < c и равна cμ при n ≥ c . Можно рассмотреть одноканальную систему (M_n /M_n /1):(GD/∞/∞) с интенсивностями входного и выходного потоков λ_n = λ и μ_n = nμ (n < c) иди μ_n = cμ (n ≥ c), а такого вида система рассматривалась выше.

Для модели системы (M_n /M_n /1):(GD/∞/∞) справедливы утверждения:

• P{в системе n заявок, в интервале h нет новых поступлений} ≈ 1 – λ_n h;

• P{в системе n заявок, в интервале h нет ни одного выбытия} ≈ 1 – μ_n h.

Так как в интервале h может произойти максимум одно событие (поступление или выбытие), то справедливы соотношения

p_n(t + h) ≈ p_n(t)( 1 – λ_n h)( 1 – μ_n h) + p_{n - 1}(t)( λ_{n – 1}h)( 1 – μ_{n – 1}h) +

+p_n+1(t)( 1 – λ_n+1 h)(μ_n+1 h), n > 0,

p₀(t + h) ≈ p₀(t)( 1 – λ₀ h)( 1) + p₁(t)( 1 – λ₁ h)(μ₁ h), n = 0.

Полагая, что при t →∞ функционирование СМО переходит в стационарный режим, при котором ;p_n(t) → p_n ,то вышеприведенные соотношения можно записать в виде:

p₁ = λ₀ p₀ /μ₁,

p_n+1 =

Рассматривая последовательно соотношения для p₁, p₂, … и применяя метод математической индукции можно получить

(3.3.23)

Выражение для p₀ получается из условий нормировки ∑ p = 1.

Обозначенный выше подход позволяет также сводить анализ модели СМО (M/M/N):(GD/M/∞) на основе системы (M_n /M_n /1):(GD/M/∞), где M – максимальная ёмкость очереди. Приведём некоторые важные соотношения для основных характеристик этой СМО.

Вероятность того, что в системе занято ровно k (0 < k < N) обслуживающих устройств

P_k = , (3.3.24)

т. е. ρ – среднее число заявок на среднее время обслуживания (приведённая плотность потока заявок).

При k = 0 и k = N из соотношения (3.3.24) получаем формулы для вычисления P₀ – вероятности того, что все обслуживающие устройства свободны; и P_N = P_отк. – вероятности того, что все обслуживающие устройства заняты, равной вероятности отказа очередной заявке в обслуживании:

P₀ = P_N = P_отк = . (3.3.25)

Среднее число занятых ослуживающих устройств

m_k = Mk = 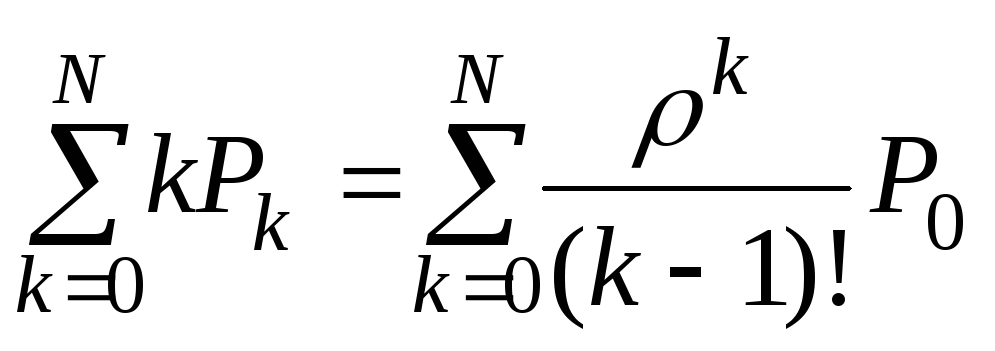. (3.3.26)

Если на рассматриваемую СМО наложить дополнительное ограничение на режим очереди: предполагается, что время ожидания заявок ограниченовеличиной T_ож. и распределено по показательному закону с параметром γ = =1/m_{t ож} (величина параметра обратна среднему времени ожидания). Основные показатели такой СМО:

Вероятность P_k того, что занято точно k обслуживающих устройств (очереди нет):

P_k = (ρ^k/k!)P₀ , 0 < k ≤ N. (3.3.27)

Вероятность P_n+s того, что все n аппаратов заняты, s заявок стоят в очереди:

P_N+s = . (3.3.28)

Вероятность P₀ того, что все аппараты свободны:

P₀ = . (3.3.29)

Средняя длина очереди

m_s = Ms = = . (3.3.30)

Вероятность P_н.о. того, что заявка покинет систему не обслуженной:

P_н.о. = . (3.3.31)

Имеет смысл напомнить, что в приведённых выше формулах использованы обозначения: N – число обслуживающих устройств в данной СМО;

где λ – плотность простейшего потока заявок, μ – па-

раметр показательного времени обслуживания (величина, обратная среднему времени обслуживания), γ – параметр показательного времени ожидания (величина, обратная среднему времени ожидания).

Следует обратить внимание, что рассматриваемая СМО при β → ∞ переходит в СМО с отказами; при β → 0 – в «чистую» систему с ожиданием, когда заявки вообще не уходят из очереди (бесконечное время ожидания, но каждая из заявок рано или поздно будет обслужена).

Замечание 3.4. В последней рассмотренной СМО стационарный режим существует только при ρ < N (λ < μN) (см. Замечание 3.2). В противном случае число заявок в очереди с течением времени неограниченно возрастает.

Для СМО с неограниченным временем ожидания при ρ < N справедливы соотношения для установившегося предельного режима:

• вероятность P₀ того, что все аппараты свободны

P₀ = (3.3.32)

• вероятность P_k того, что занято точно k обслуживающих устройств (очереди нет)

P_k = (3.3.33)

• вероятность P_N+s того, что все N аппаратов заняты, s заявок стоят в очереди

P_N+s = (3.3.34)

• средняя длина очереди

m_s = . (3.3.35)

И последнее: если имеется СМО с ожиданием с ограничением длины очереди, то при простейшем потоке заявок и показательном распределении времени обслуживания (система (M/M/N):(GD/M/∞) с ожиданием) формулы для P_k и P_N+s соответственно имеют вид:

• вероятность P_k того, что занято точно k обслуживающих устройств (очереди нет)

P_k = . (3.3.36)

• вероятность P_N+s того, что все N аппаратов заняты, s заявок стоят в очереди

P_N+s = , (3.3.37)

где M – число заявок, которым ограничена очередь.

Замечание 3.5. В заключение хотелось бы обратить внимание на то, что СМО, в которых ничем не ограничено ни время пребывания в очереди, ни число заявок в очереди, называются чистыми системами с ожиданием. Если имеются ограничения по какому-нибудь из этих признаков, СМО называется системой смешанного типа. Приведённые выше соотношения (3.3.32 – 3.3.35) описывают установившийся режим чистой системы с ожиданием. Формулы (3.3.36, 3.3.37) в свою очередь описывают систему массового обслуживания смешанного типа с ограничениями по числу мест в очереди. Второй вариант каждой из формул соответствует случаю ρ < N, хотя установившийся режим в этом случае достигается при всех соотношениях параметров.

Ограничения по времени пребывания заявки в очереди (или в системе) при составлении уравнений для вероятностей состояний учитываются тем, что на каждую заявку, находящуюся в очереди (системе), действует «поток уходов» с плотностью ν, обратной среднему времени пребывания заявки в очереди.