
- •И математической статистике
- •Ч а с т ь III
- •2. Описание случайных процессов и полей
- •3. Представления и преобразования случайных функций
- •4. Стационарность и однородность случайных функций;
- •5. Непрерывность, дифференцируемость и интегрируемость
- •6. Спектральное представление случайных процессов и полей
- •§2. Марковские процессы
- •2.1. Последовательности зависимых испытаний. Цепи Маркова.
- •2.2. Марковские процессы.
- •§3. Элементы теории систем массового обслуживания (смо)
- •3.1. Основные понятия, определения и компоненты моделей смо
- •3.2. Потоки событий.
- •3.3. Классификация смо и их основные характеристики
- •Раздел 2. Вариаты практических заданий задачи для самостоятельного решения
- •Раздел 3. Решения вариатов типовых заданий задача 1.
- •Задача 2.
- •Задача 3.
- •Задача 4.
- •I. Свойства дельта- функции и некоторых других обобщённых функций
- •II. Использование таблиц распределения пуассона при решении задач смо
- •III. Статистические таблицы
- •Примечания:1) функция Лапласа и интеграл ошибоксвязаны соотношением;
- •Содержание
- •Часть III
Раздел 3. Решения вариатов типовых заданий задача 1.
1. X(t) – случайный процесс с независимыми приращениями X(t′) – X(t), распределёнными по нормальному закону с нулевым математическим ожиданием и дисперсией σ2 = (t′) – t (винеровский процесс). Пусть X(0) = 0. Найти математическое ожидание, дисперсию и корреляционную функцию процесса Винера.
Р Е Ш Е Н И Е:
Очевидно,
P{X(t)
< x}
= P{X(t)
– X(0)
< x}
=
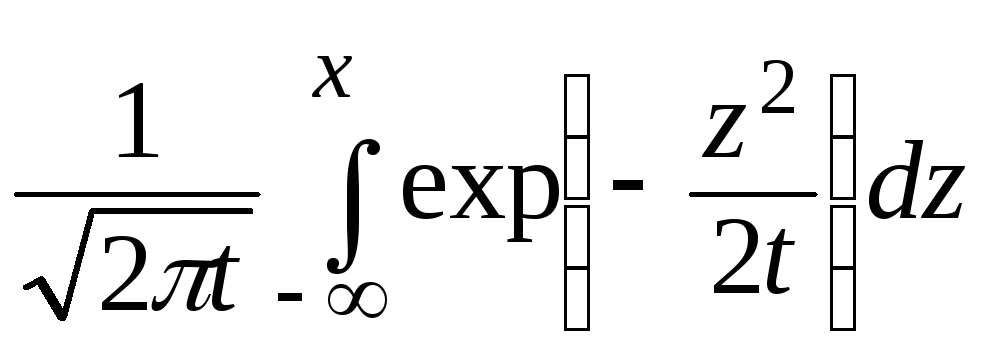 ,
,
поэтому
одномерная плотность вероятности
процесса X(t)
будет f1
(x;
t)
= = .
Далее, если известно значение процесса
X(t')=
x,
то распределение X(t')
при любом
t'
>
t
совпадает
с распределением [X(t')
– X(t)]
+ X(t)
и не зависит от предшествующего (до
момента t).
Следовательно, процесс X(t)
– марковский (без последствия), а тогда
для полной вероятностной характеристики
его достаточно двумерной плотности
f2(x,
y;
t,
t').
По условию, если известно значение xi
– 1,
принятое сечением процесса X(ti
– 1),
то условная плотность сечения X(ti)
,будет f2
(xi,
ti
|
xi
– 1,
ti
–1).
Но f2(x1,
x2;
t,
t')
= f1
(x1;
t)
× × f2
(x2,
t'
|
x1,
t)
поэтому f2
(x1,
x2;
t,
t')
=
.
Далее, если известно значение процесса
X(t')=
x,
то распределение X(t')
при любом
t'
>
t
совпадает
с распределением [X(t')
– X(t)]
+ X(t)
и не зависит от предшествующего (до
момента t).
Следовательно, процесс X(t)
– марковский (без последствия), а тогда
для полной вероятностной характеристики
его достаточно двумерной плотности
f2(x,
y;
t,
t').
По условию, если известно значение xi
– 1,
принятое сечением процесса X(ti
– 1),
то условная плотность сечения X(ti)
,будет f2
(xi,
ti
|
xi
– 1,
ti
–1).
Но f2(x1,
x2;
t,
t')
= f1
(x1;
t)
× × f2
(x2,
t'
|
x1,
t)
поэтому f2
(x1,
x2;
t,
t')
=
 приt'
>
t.
Тогда, математическое
ожидание процесса
mx(t)
=
приt'
>
t.
Тогда, математическое
ожидание процесса
mx(t)
=![]() в силу чётности функции f1
(x;
t);
корреляционная
функция Kx
(t,
t')=
=
в силу чётности функции f1
(x;
t);
корреляционная
функция Kx
(t,
t')=
= =
t,
но так как Kx(t,
t')
=
=
t,
но так как Kx(t,
t')
=
=
Kx(t,
t')
то окончательно Kx(t,
t')
=
 Тогдадисперсия
процесса
Тогдадисперсия
процесса
Dx(t) = Kx(t, t) = t. ◊
2. Случайная функция Х(t) задана каноническим разложением X(t) = t – 3cost + U (t + cost) + Vcos2t; DU = 1; DV = 2. Найти математическое ожидание M Х(t), дисперсию D Х(t) и корреляционную функцию Kx(t, t′)
Р Е Ш Е Н И Е:
Используя соотношения (1.3.7) – (1.3.9) и данные задачи получаем:
MX(t) = mx(t) = t – 3 cos t; Kx(t, t') = (t + cos t) (t' + cos t') + 2 cos 2t cos 2t' ;
Dx(t) = (t + cos t)2 + 2 cos2 t. ◊
3.
Дана случайная
функция X(t)
= x1t
+ x2
sint,
где случайный вектор (x1,
x2)
имеет математическое ожидание (+1, – 1)
и корреляционную матрицу
![]() .
Построить каноническое разложение этой
случайной функции; найти её математическое
ожидание, корреляционную функцию и
дисперсию.
.
Построить каноническое разложение этой
случайной функции; найти её математическое
ожидание, корреляционную функцию и
дисперсию.
Р Е Ш Е Н И Е:
Используя те же соотношения, что указаны в решении предыдущей задачи, а также данные задачи, запишем MX(t) =mx(t) =t – sint;X(t) = (x1– 1)t+ (x2 + 1) ×sint + t–sint;x1– 1 =U,x2 + 1 =aU+V,MU = MV =0,DU =Dx1= 2. Коэффициентaподбирают так, чтобыUиVбыли некоррелированы:
M[(x1– 1)(x2 + 1)] =aMU2+M(UV) = 1 по условию. ПолагаяM(UV) = 0, находимa =½. Таким образом,x1– 1 =U,x2 + 1 =½U+V,X(t) =t–sint + U(t+ +½ sint)+ Vsint–каноническое разложение. ОтсюдаKx(t, t') =DU(t+½ sint) (t'+½ sint') +DVsintsint' = 2(t+½ sint) (t'+½ sint') + 2,5sintsint';Dx= 2(t+½ sint)2+ 2,5sin2t. ◊
4. Вычислить математическое ожидание и ковариационную функцию случайного двоичного сигнала ξ(t), сформированного на основе простого пуассоновского потока упорядоченных временных точек {tk , k = 0, 1, 2, …} следующим образом ξ(t) = 1, если число точек в интервале (0, t) чётное, и ξ(t) = – 1, если число точек в интервале (0, t) нечётное.
Р Е Ш Е Н И Е:
Так как события {kточек в (0,t)} при различныхk= 0, 1, 2, … несовместны, то вероятность наличия чётного числа точек в интервале (0,t) в соответствии с законом Пуассона равнаp0 (t)+ p2(t) + … =e – λt [1 + (λt)2/2! + …] =
= e – λt ch(λt). Аналогично, вероятность получения нечётного числа точек в интервале (0,t) равнаp1 (t)+ p3(t) + … =e – λt [λt+ (λt)3/3! + …] =e – λt sh(λt). СледовательноP{ξ(t) = 1} =e – λt ch(λt),P{ξ(t) = –1} =e – λt sh(λt). Таким образом,математическое ожидание данного процессаM[ξ(t)] = mx(t)= 1· P{ξ(t) = 1} – 1· P{ξ(t) = –1} =e – λt (ch(λt) –sh(λt)) =e – 2λt, откуда, в частности, следует, этот процесснестационарен.
Для вычисления ковариационной функцииKξ(t1, t2) =M{ξ(t1)·ξ(t2)} нуж-но знать совместные вероятности случайных величинξ(t1) иξ(t2). Распишем их. Пустьt1–t2=τ> 0. При заданном значенииξ(t2) = 1 случайная величинаξ(t1) = 1, если в интервале (t2,t1) имеется чётное число точек. Поэтому условная вкроятностьP{ ξ(t1) = 1| ξ(t2) = 1} =e – λτ ch(λ τ). Умножив это выражение наP{ξ(t2) = 1}, получимP{ ξ(t1) = 1, ξ(t2) = 1} =e – λτ ch(λτ)·e – λt2 ch(λt2). Аналогично находим P{ ξ(t1) = –1, ξ(t2) = –1} =e – λτ ch(λτ)·e – λt2 sh(λt2); так как
P{ ξ(t1) = 1| ξ(t2) = –1} =e – λτ sh(λτ), тоP{ ξ(t1) = 1, ξ(t2) = –1} =e – λτ sh(λτ)·e – λt2· ·sh(λt2),P{ ξ(t1) = –1, ξ(t2) = 1} =e – λτ sh(λτ)·e – λt2 ch(λt2). Записав развёрнутое выражение для ковариационной функции и подставив в него найденные вероятности, находимKξ(t1, t2) =exp[– 2λ(t1–t2)]. Меняяt1иt2местами (т. е. полагаяt1<t2), окончательно находимKξ(τ) = exp[– 2λ| τ|], τ =t2 – t1.
Примечание. Нестационарность рассмотренного процесса объясняется тем, что начало отсчёта выбрано вполне определённым образом – на положительном импульсе. Чтобы «начальное условие» было случайно выбранным, удобно рассматривать случайную величину η(t) = Aξ(t), где A – независимая от ξ(t) случайная величина, принимающая лишь два зачения: 1 и – 1 с одинаковыми вероятностями ½. При этом M[A] = 0, M[A2] = 1. Нетрудно убедиться, что процесс η(t) стационарен, т. к. M[η(t)] = 0; при этом Kη(t1, t2) = M[A2] M{ξ(t1)·ξ(t2)} = Kξ(t1, t2) = exp[– 2λ| τ|],
τ =t2 – t1. ◊
5.
Случайная функция
X(t)
имеет характеристики: математическое
ожидание mx(t)
= 0; корреляционную функцию Kx(t,
t')
=
![]() .
Найти характеристики случайной функцииY(t)
=
.
Найти характеристики случайной функцииY(t)
=
 .
.
Р Е Ш Е Н И Е:
В
силу линейности преобразования
 имеем:my(t)
=
имеем:my(t)
=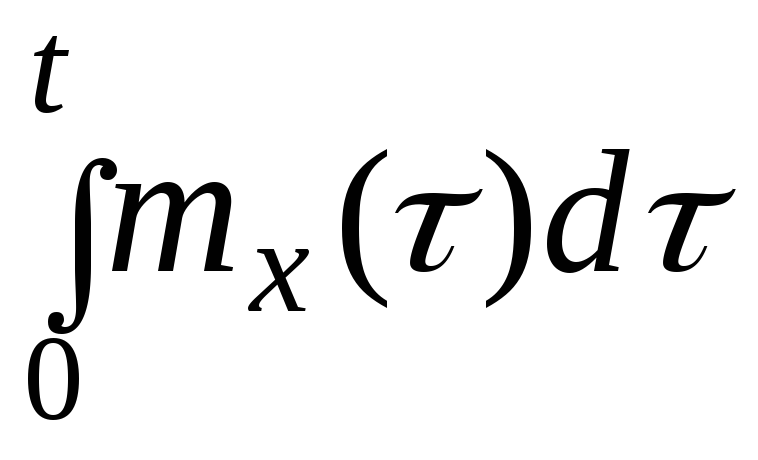 =
0,Ky(t,
t') =
=
0,Ky(t,
t') =

 =
=
=
t arctg t
+t' arctg t'
– (t –
t') arctg (t
– t') – ½
ln
 .
.
Полученный результат показывает, что хотя исходная случайная функциястационарна(Kx(t, t') = Kx(t, t') =Kx(τ) =Kx(t' – t) ), после преобразования получаемнестационарный случайный процесс: его дисперсияDy(t) = 2t arctgt – ln(1 +t2), то есть зависит отt. ◊
6. Будем считать, что при качке судна угол крена корабля есть стационарный и нормальный случайный процесс X(t) с нулевым математическим ожиданием и корреляционной функцией
 .
.
Сколько раз в среднем за T = 20 мин. Хода судна угол крена будет выходить за пределы [– 25°, 25°], если A = 100 град2, α = 0,1 1/с, β = 0,7 1/с? Найти, сколько раз в среднем в течении 10 мин. угол крена будет равен 0.
Р Е Ш Е Н И Е:
ИмеемDx = σ2=Kx(0) =A= 100. Рассмотрим случайный процесс
ν(t)
=X '(t)
= dX(t)
/dt. Тогда![]()
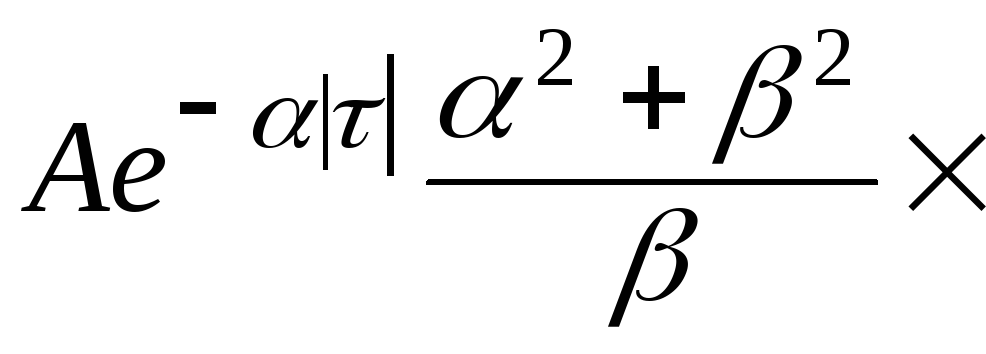
![]() ;
Dν=σν2=Kν(0)
=A(α2+β2). Тогда
среднее число выбросов за уровеньaв единицу времени определяется по
формуле (см. (1.6.29))
;
Dν=σν2=Kν(0)
=A(α2+β2). Тогда
среднее число выбросов за уровеньaв единицу времени определяется по
формуле (см. (1.6.29))
 ;
;
так как нужно учитывать уклонение угла крена за 25○по абсолютной величине, то для среднего числа таких уклонений получим (см. (1.6.28))
![]() .
Среднее число выбросов за нулевой
уровень
.
Среднее число выбросов за нулевой
уровень 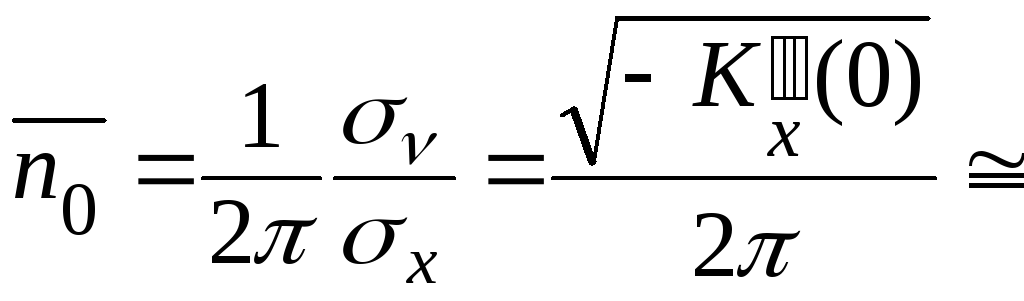 0,225 (1/с). ◊
0,225 (1/с). ◊
