I. Свойства дельта- функции и некоторых других обобщённых функций

При решении задач, связанных со случайными функциями, часто бывает удобно или приходится выполнять преобразования с помощью различных скачкообразных функций, а также обобщённых функций типа дельта-функции.

Здесь приводятся определения и основные свойства таких функций от действительного аргумента τ.

1. | τ | – модуль (абсолютная величина):

| τ | =

2. l(τ) – единичная функция (единичный скачок):

l(τ) =

3. sign τ – знак величины τ (сигнум):

sign τ =

4. δ(τ) – дельта-функция:

δ(τ) = (= ).

Дельта-функция – чётная функция τ. Основные свойства дельта-функции:

а) τ δ(τ) ≡ 0 и вообще φ(τ) δ(τ) ≡ 0, если φ(τ) – нечётная функция, непрерывная при τ = 0.

б) ,если функция ψ(t) непрерывна в точке τ = 0

(ε > 0),,если ψ(t) непрерывна в точке τ =0, и вообще φ(τ) δ(τ – τ₀) = φ(τ₀), если φ(t) непрерывна в точке τ₀.

c) , то есть можно записать

= .В более общем случае, если α(τ) – монотонная на

интервале (a, b) функция, то δ[α(τ)] = δ(τ – τ₀)/ [α'(τ₀)]

Из этих определений вытекают следующие свойства, имеющие место для любых действительных τ и нечётной функции ψ(t):

1. | τ | = τ sign τ ; 2. τ = | τ | sign τ ; 3. φ(τ) = φ(| τ |) sign τ;

4. φ(| τ |) = φ(τ) sign τ; 5. φ²(| τ |) = φ²(τ); 6. sign τ = 2·l(τ) – 1;

7. l(τ) = 0,5 (sign τ + 1); 8. | τ | = 2[l(τ) – 1]; 9. ;

10. ;11.l(τ) =;

12. Для нечётных положительных k (sign τ)^k = sign τ. Для чётных по ложительных k (sign τ)^k =

13.

14.

15.

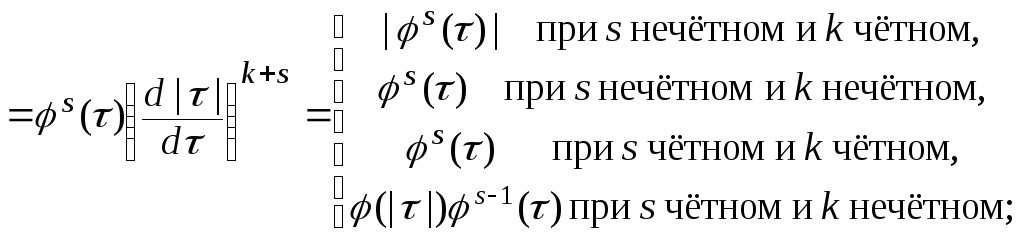
16.

II. Использование таблиц распределения пуассона при решении задач смо

В ряде случаев удобно использовать обозначения, позволяющие при расчётах других характеристик широко применять таблицы распределения Пуассона – так называемые формулы Эрланга.

Плотность распределения для промежутков времени между событиями в потоке Эрланга

,

где P(k,λt) – функция распределения Пуассона с соответствующими параметрами; кроме того, используются функцииR(k,λt) =, для которой также имеются таблицы, иQ(m,a) = 1 –R(m,a). В этих обозначениях функция распределения ЭрлангаF_k(t) = 1 –R(k,λt) =Q(k,λt). Справедливы следующие соотношения:P(k,a) =R(k,a) –R(k – 1,λa) =Q(k – 1,a) –Q(k,a);

.

В этом случае, например формула (3.3.24) P_k = , где , обретает вид P_k = P(k, ρ)/ R(n, ρ) =,k =1, 2, …, n. В частности, вероятность того, что заявка будет обслужена (не получит отказа) P_обс. = 1 – P_n = 1 – . Вероятности того , что в системе заняты ровно k обслуживающих устройств, и что всистеме нет свободных мест в общем случае задаются формулами:

P_k=;P_{N +s}=.Прежде всеговеличина =, гдеρ =λ/μ; γ = λ/ν = ρ/β; δ = Nμ/ν = γ/ρ = N/β; –гамма-функция, для которой, как известно Γ(x + 1) = x Γ(x). Если величина δ – целое число, то =,=

==. Тогда

P_k=;

P_{N +s}= .

Большинство приведённых соотношений получено в предположении, что δ – целое число. Если это не так, то вычисление можно произвести для двух ближайших к величине δ целых чисел и произвести между вычислениями линейную интерполяцию. Такой приём даёт удовлетворительные по точности результаты.

Если число мест в очереди не ограничено (m → ∞), то формулы упрощаются с учётом того, что

Если заявки, попавшие в очередь не покидают её, а «терпеливо» ожидают начала обслуживания (т. е. δ =∞,ν =0, а значит и β =0), то

P_k=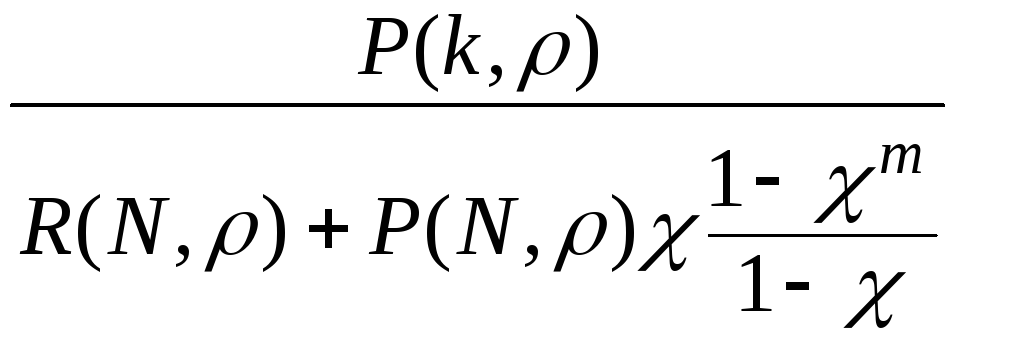;P_{N +s}=, где. В такой системе при отсутствии ограничений на число мест в очереди (m → ∞), стационарный режим возможен только приχ< 1:

P_k=;P_{N +s}=. Вероятность обслуживания во всех случаяхP_обс= 1 –P_{N + m}.