Раздел 2. Вариаты практических заданий задачи для самостоятельного решения

Вариант 1.

1. Случайный процесс Х(t) имеет математическое ожидание M X(t) =

=2t + 1 и корреляционную функцию K_x(t′, t) = exp{– (t′– t)}. Найти математическое ожидание, корреляционную функцию и дисперсию случайного процесса Y(t) = d Х(t)/dt.

2. Случайный процесс Х(t) имеет спектральную плотность S(ω) = =. Найти корреляционную функцию этого процесса.

3. Простая однородная цепь Маркова с двумя состояниями управляется матрицей , P₁ ≠ 0, P₂ ≠ 0. а) Составить характеристическое уравнение и найти характеристические числа матрицы перехода. б) Найти финальные вероятности Ṕ₁ и Ṕ₂.

4. На вход системы обслуживания поступает простейший поток заявок с плотностью ν = 4 заявки в час. Время обслуживания обслуживание распределено по показательному закону со средним временем обслуживания одной заявки Mt_об = 15 мин. Определить:

а) необходимое количество обслуживающих устройств, чтобы вероятность отказа в обслуживании не превышала 0,01;

б) среднее число занятых обслуживающих устройств;

в) вероятность P{k ≥ 3} того, что будет занято не менее трёх устройств.

Вариант 2.

1. Найти математическое ожидание, дисперсию и корреляционную функцию синусоиды постоянной частоты ω со случайной амплитудой X, еслиMX= 1,DX = 0,2.

2. Случайный процесс Х(t) имеет спектральную плотность

S(ω) = . Найти дисперсию процесса.

3. Простая однородная цепь Маркова с тремя состояниями управляется матрицей . а) Эргодична ли эта цепь? б) Найти финальные вероятности.

4. На станцию текущего ремонта автомобилей поступает простейший поток заявок с плотностью ν = 0,5 машины в час. Имеется одно помещение для ремонта. Во дворе станции, ожидая очереди, могут одновременно находится не более трёх автомобилей. Среднее время ремонта одной машины τ_об =2 час. Определить:

а) пропускную способность этой системы автосервиса;

б) среднее время простоя станции;

в) как изменятся эти характеристики, если оборудовать второе помещение для ремонта (а если ещё и расширить площадку ожидания до 5 машин)?

Вариант 3.

1. Найти математическое ожидание, дисперсию и корреляционную функцию процесса X(t) =ξexp( –t²), гдеξ– случайная величина сMξ= 2,Dξ= 0,01.

2. Существует ли стационарный случайный процесс, корреляционная функция которого определена формулой

,

где σ² – положительная постоянная. K_x(τ) = σ², при 0 ≤ τ < Т.

3. Вероятности перехода в простой однородной цепи Маркова даются матрицей .а) Чему равно число состояний этой цепи?

б) Эргодична ли эта цепь? в) Найти вероятности перехода из состояния в состояние за два шага. г) Определить финальные вероятности; зависят лиони отначальных.

4. Имеется система массового обслуживания, функция распределения F₁(t) времени обслуживания T_об которой можно описать выражением F₁(t) = 1 – (1 + t) ^{– 2} , где – время в минутах. Определить:

a) вероятность P₁ того, что время обслуживания заявки не превзойдёт 5 мин;

б) среднее время обслуживания одной заявки;

в) вероятность P₂ того, что за это время обслуживание очередной заявки будет закончено.

Вариант 4.

1. Найти математическое ожидание, дисперсию и корреляционную функцию процесса X(t) = Ut + Vt², где U и V – некоррелированные случайные величины с MU= 3,DU = 1,MV= 0,5,DV = 0,05.

2. Случайный процесс Х(t) имеет спектральную плотность, в виде раз-ложения на простейшие дроби:

S(ω) = . Найти корреляционную функцию этого процесса.

3. На некотором острове погода бывает в течении дня или дождливой (Д) или сухой (С) т.е. представляет собой однородную цепь Маркова с двумя состояниями. Вероятности ежедневных изменений заданы матрицей

Д С

. а) Если в среду погода дождливая, то какова вероятность что она будет дождливой в ближайшую пятницу? б) Как изменится ответ на этот вопрос, если дождливая погода в среду ожидается с вероятностью 0,3?

4. Нестационарный пуассоновский поток вызовов на телефонную станцию имеет мгновенную плотность вида ν(t) =ν(1 –cos2at). Найти среднюю плотность вызовов в интервале времени отt₀ до t₀ + t.

Вариант 5.

1. Найти математическое ожидание, дисперсию и корреляционную

функцию случайной функции X(t) = x₁cosωt + x₂sinωt +5t, где x₁ и x₂ – некоррелированные случайные величины с Mx₁= 1;Dx₁ = 0,1;Mx₂= 0,2;Dx₂ = 0,004;ω – положительная постоянная.

2. Случайный процесс Х(t) имеет спектральную плотность

S(ω) = . Найти дисперсию процесса.

2. Простая однородная цепь Маркова с двумя состояниями управляется матрицей . Убедиться в регулярности цепи и найти финальные вероятностиṔ₁ и Ṕ₂.

4. Мгновенная плотность ν(t) нестационарного пуассоновского входного потока заявок представляет собой линейную функцию времени ν(t) = a + bt. Определить плотность вероятности случайной величины T – промежутка времени между соседними заявками.

Вариант 6.

1. X(t) – случайный процесс с независимыми приращениями X(t′) – X(t), распределёнными по нормальному закону с нулевым математическим ожиданием и дисперсией σ² = (t′) – t (винеровский процесс). Пусть X(0) = 0. Найти математическое ожидание, дисперсию и корреляционную функцию процесса Винера.

2. Найти функцию корреляции К_ξ(τ) стационарного случайногопроцесса ξ(t) со спектральной плотностью

₀,₁ ₂;

S_ξ(ω) =₀,₂ ₁;S_ξ(ω)

0, все другие.

Для частного случая_0 определить величину

интервала= t_k+1– t_k при котором значения ξ_k+1=₀/2 N₀/2

=ξ(t_k+1) и ξ_k= ξ(t_k) некоррелированы.–ω₁ –ω₂ ω₂ ω₁ ω

3. Марковская цепь с двумя состояниями S₁и S₂задана матрицей

вероятностей переходов Некое устройство с вероятностьюрвыбирает в качестве начала процесса состояние S₁ и с вероятностью (1 – р) – выбирает S₂. Найти вероятность того, что после первого шага процесс будет в состоянии S₂, если а)р= 1/2; б)р= 1/3.

4. Проектируемое радиотехническое устройство должно содержать три последовательно соединенных блока. Расчёты показали, что интенсивности отказов первого и второго блока составят ν₁= 0,008час ^{– 1}и ν₂= 0,0032 час ^{– 1}. Время безотказной работы каждого из блоков распределено по показательному закону. Определить необходимую величину интенсивности отказов третьего блока, чтобы вероятность безотказной работы устройства в течении времениt= 1часравнялась 0,95.

Вариант 7.

1. Дана случайная функция X(t) =x₁t + x₂ sint, где случайный вектор (x₁, x₂) имеет математическое ожидание (+1, – 1) и корреляционную матрицу. Построить каноническое разложение этой случайной функции; найти её математическое ожидание, корреляционную функцию и дисперсию.

2. Спектральная плотность S_ξ(ω) стационарного случайного процесса ξ(t) имеет вид: S_ξ(ω) =Определить соотношение между энергетической полосойW_э=процесса ξ(t) и шириной его спектральной плотностина уровне 0,5 S_ξ(0).

3. Доказать, что все стационарные однородные цепи Маркова с двумя состояниями, задаваемые матрицами перехода вида π = , имеют одинаковые стационарные (финальные) вероятности и найти их.

4. В счётчике Гейгера – Мюллера для подсчёта космических частиц частица, попавшая в счётчик, вызывает разряд, длящийся время τ (τ постоянно). Попавшие в это время в счётчик новые частицы счётчиком не регистрируются.

Считая, что распределение числа частиц, попавших в счётчик, подчиняется закону Пуассона, найти вероятность того, что счётчик за время t> 0 сосчитает все попавшие в него частицы.

Вариант 8.

1. Дана случайная функция X(t) =t+x₁cost + x₂ sint, где случайный вектор (x₁, x₂) имеет математическое ожидание (– ½, 1) и корреляционную матрицу. Построить каноническое разложение этой случайной функции; найти её математическое ожидание, корреляционную функцию и дисперсию.

2. Стационарный случайный процесс X(t) имеет спектральную плотность, равную нулю вне промежутка частот (ω_1,ω₂) и постоянную на этом промежутке. Найти коэффициент корреляции двух произвольных сечений этого процесса.

3. Простая однородная цепь Маркова с тремя состояниями управляется матрицей . Убедиться в регулярности цепи и найти финальные вероятности Ṕ₁ , Ṕ₂и Ṕ₃.

4. Группа из nсамолётов производит поиск малоразмерного объекта. Каждый самолёт действует независимо от других, но поиск прекращается, как только объект будет обнаружен одним из самолётов.

Пусть закон распределения времени поиска каждым самолётом – показательный, причём среднее время поиска для каждого самолёта соответственно равно 1/μ_k,k=1, 2, …,n. Показать, что функция распределения времени поиска всемиnсамолётами имеет видF₁(t) = 1 –exp{– (μ₁+μ₂+ … +μ_n)t}. Для случаяμ₁= =μ₂= … =μ_n=μ найти математическое ожидание и дисперсию времени поиска

Вариант 9.

1. Случайная функция Х(t) задана каноническим разложениемX(t) =t– 3cost + U (t + cost) +Vcos2t;DU =1; DV =2. Найти математическое ожиданиеM Х(t), дисперсиюD Х(t) и корреляционную функциюK_x(t, t′)

2. Случайные процессы Х₁(t) иХ₂(t) имеет спектральные плотности

S₁(ω) =и S₂(ω) =. Найти отноше-ние корреляционных функцийK₂(τ)/K₁(τ) этих процессов.

3. Дана простая однородная цепь Маркова с двумя состояниями, матри-ца перехода которой имеет вид: π = ,p₁ ≠ 0, p₂ ≠ 0.

Сравнить стационарные (финальные) вероятности этой цепи для случа-ев: а) 0 ≠ p₁ ≠ p₂ ≠ 1; б) 0 ≠ p₁ = p₂ ≠ 1; в) 0 ≠ p₁ = 1 – p₂ ≠ 1. Частный случай p₁ или p₂ = 0 или 1 во всех этих случаях рассмотреть отдельно.

4. На автопарковку, рассчитанную на n мест, прибывает простейший поток машин с интенсивностью ν до тех пор, пока имеются свободные места. Полагая поток покидающих парковку автомобилей также простейшим с интенсивностью μ, записать дифференциальные уравнения для вероятностей P_k(t) того, что ровно k мест заняты

Вариант 10.

1. Дана случайная функция X(t) =t+x₁cost + x₂ sint, где случайный вектор (x₁, x₂) имеет математическое ожидание (– ½, 1) и корреляционную матрицу. ПустьY(t) = . Найти математическое ожидание, корреляционную функцию и дисперсию процессаY(t).

Указание: Построить каноническое разложение этой случайной функции.

2. Существует ли стационарный случайный процесс, корреляционная функция которого определена формулой

,

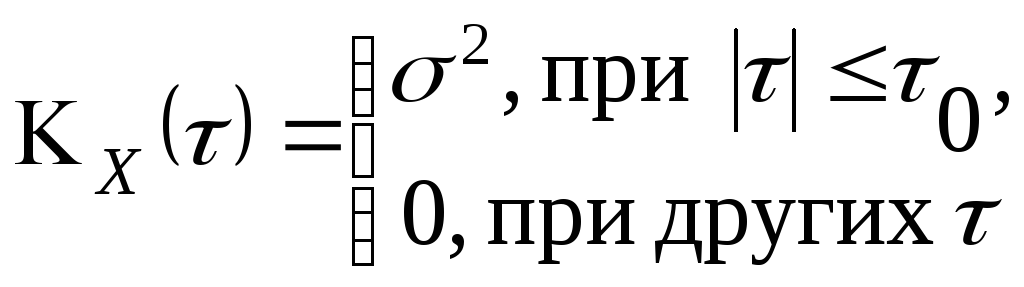где σ²– положительная постоянная. Какова в случае положительного ответа спектральная плотность этого процесса.

3. Вероятности перехода в простой однородной цепи Маркова даются дважды стохастической матрицей .а) Чему равно число сос-тояний этой цепи? б) Эргодична ли эта цепь? в) Найти вероятности перехода

из состояния в состояние за два шага. г) Определить финальные вероятности; зависят ли они от начальных?

4. Сколько оборонительных комплексов nдолжна иметь оборонительная система, чтобы вероятность её прорыва противником не превышала 0,02, если на данном направлении действует простейший поток целей противника с плотностью ν = 4, время обстрела одной цели одним оборонительным комплексом распределено по показательному закону с параметром μ = 2, а вероятность поражения цели при одном выстреле (залпе) равна единице

Вариант 11.

1. На вход интегрирующего устройства поступает случайный процесс, имеющий каноническое разложение X(t) = 1 + Ut + Vt²; DU = 3; DV = 1. Найтиматематическое ожидание, корреляционную функцию и дисперсию процесса на выходе интегратора.

2. Случайный процесс Х(t) имеет корреляционную функцию K_x(τ) =

= σ²e ^–α|τ|[cos(ω₀τ) + (α/ω₀)sin(ω₀τ)] . Найти спектральную плотность этого процесса.

3. Простая однородная цепь Маркова с двумя состояниями управляется матрицей . Убедиться в регулярности цепи и найти финальные вероятности Ṕ₁ и Ṕ₂.

4. Число отказов радиотехнической системы представляет собой простейший поток с интенсивностью 0,005 ¹/час. Вычислить:

а) вероятность безотказной системы за t= 20час;

б) математическое ожидание и дисперсию времени безотказной работы системы.

Вариант 12.

1. На вход интегрирующего устройства поступает случайный процесс X(t) с M X(t) = 0,2 cos²ωt и K_x(t, t′) = 0,4 cosωt cosωt′. Найти математическое ожидание, корреляционную функцию и дисперсию процесса Y(t) на выходе интегратора.

2. Стационарный случайный процесс Х(t) имеет спектральную плот-ность S(ω) =.Найти корреляционную функцию R(τ) процесса, а

также время корреляции τ_кор..

3. Точка в начальный момент времениt₀= 0 с вероятностью 1/5 находится в одной из точекx = 0, 1, 2, 3, 4. В моменты времени 0 <t₁<t₂< … <t_k< … точка, в зависимости от случая, может совершать скачок длиной 1 влево с вероятностьюp или вправо с вероятностью q = 1 – pсоответственно, если она не находилась непосредственно перед этим скачком в точкахx= 0 иx = 4. В этих двух последних случаях движение точки прекращается.

a) Чему равно число состояний этой цепи?b) Написать матрицу вероятностей перехода этой цепи Маркова.c) Найти вероятности перехода из состояния в состояние за два шага. г) Эргодична ли эта цепь?

4. Обозначим через ν_tслучайное число требований пуассоновского потока, поступивших в интервале [0,t). Доказать, что приt ≤ T, k ≤n

P(ν_t=k | ν_T = n) = .

Вариант 13.

1. Дана случайная функцияX(t) =x·exp(βt)·cosωt, гдеx– случайная величина сMx = 3,Dx =1,β и ω – постоянные. Найти математическое ожидание, корреляционную функцию и дисперсию случайной функцииY(t) = =.

2. Случайный процесс Х(t) имеет спектральную плотность

S(ω) = . Найти корреляционную функцию этого процесса и время корреляции.

3. Простая однородная цепь Маркова с тремя состояниями управляется матрицей . а) Эргодична ли эта цепь? б) Найти финальные вероятности.

4. Найти вероятность P₀(t) свободного состояния в момент t системы

M|M|1|0, если интенсивность входящего потока равна λ, среднее время обслуживания – ¹/μ и:

а) в момент t =0 система была свободна;

б) в момент t =0 система была занята.

Вариант 14.

1. Пусть φ – случайная величина, равномерно распределённая на отрезке [0, 2π],a и ω– положительные постоянные. Доказать, что случайный процессX(t) =asin(ωt +φ) стационарный (в широком смысле) и эргодичный (относительно своего математического ожиданияm_x и корреляционной функцииK_x(τ)). Пользуясь этим, найтиm_x иK_x(τ).

2. Стационарный случайный процесс X(t) имеет корреляционную функцию

Найти спектральную плотность процесса X(t).

3. Пусть точка в начальный момент t₀= 0 с вероятностью 1/(n+ 1) находится в любой из точекx = 0, 1, 2, …,n. В моменты времени 0 <t₁< t₂< … < t_k< … точка, в зависимости от случая, может совершать скачок длиной 1влевос вероятностьюpивправо – с вероятностьюq =1 – p, если она не находилась непосредственно перед этим скачком в точках x = 0 иx = n.

В этих двух последних случаях движение точки прекращается.

а) Написать матрицу переходных вероятностей этой цепи Маркова.

б) Выяснить, является ли эта цепь регулярной, и дать характеристику её состояний (случайное блуждание по прямой с поглощающими экранами).

4. На вход обслуживающей системы поступает простейший поток заявок с плотностью ν. Случайная величина T– промежуток времени между смежными заявками. Записать формулы для функции распределения, плотности вероятности, математического ожидания и дисперсии величины T.

Вариант 15.

1. Дан случайный процесс X(t) =asin(ωt +φ), гдеa и ω– положительные постоянные, φ – нормальная случайная величина сMφ =0,Dφ = 1. Будет лиX(t) стационарным процессом? Найти математическое ожидание, корреляционную функцию и дисперсию процессаX(t).

2. Стационарный случайный процессX(t) имеет корреляционную функциюK_x(τ) = e ^{– | τ |}cosβτ. Найти спектральную плотность процессаX(t).

3. Nчёрных и Nбелых шаров размещены в двух урнах по N шаров в каждой. Число чёрных шаров в первой урне определяет состояние системы. На каждом шагу случайно выбирается по одному шару из каждой урны и эти выбранные шары меняются местами.

а) Сколько состояний имеет цепь Маркова, управляющая переходами этой системы.

б) Найти все вероятности перехода за один шаг.

в) Найти их асимптотическое значение (финальные вероятности).

4. Узел связи обслуживает 100000 абонентов, каждый из которых в среднем занимает линию связи в течении 2 минут за час. Какое число nканалов надо иметь, чтобы исключить длительные ожидания (вероятность того, что максимальное число одновременно поступивших вызовов превысит число каналов, не должна превышать 0,3%)?

Вариант 16.

1. Будем считать, что при качке судна угол крена корабля есть стационарный и нормальный случайный процесс X(t) с нулевым математическим ожиданием и корреляционной функцией

.

Сколько раз в среднем за 20 мин. Хода судна угол крена будет выходить за пределы [– 25°, 25°], еслиA =100град², α = 0,1 1/с, β = 0,7 1/с?

2. Стационарный случайный процесс X(t) имеет корреляционную функциюK_x(τ) = σ²e ^{–α | τ |}(1 +α |τ |). Найти спектральную плотность процесса.

3. Пусть {ξ_n} – последовательность независимых случайных величин, имеющих одинаковую плотность распределенияp(x),p(x) > 0, – ∞ <x< ∞. Положим

S_t = S_k(t – k) + S_k+1(k + 1 – t), k ≤ t ≤ k + 1, S_n = ξ₁ + … + ξ_n

Будет ли процесс S_tмарковским?

4. Для охраны района выделено 10 кораблей, ремонт которых обеспечивают два дока. Каждый док может одновременно принять для ремонта один корабль. В док корабль ставится тогда, когда он не может нести охрану и нуждается в серьёзном ремонте. Вероятность того, что за время t (в месяцах) кораблю потребуется ремонт, равнаF(t) = 1 –exp(– 0,02t). (Корабли однотипны и одновременной постройки, поэтому их характеристики полагаются одинаковыми).

Предполагая, что в среднем на ремонт одного корабля затрачивается 2 месяца, а время ремонта подчиняется показательному закону, определить:

а) среднее число кораблей, находящихся в ремонте (включая очередь на ремонт);

б) вероятность того, что район будут постоянно охранять не менее 8 исправных кораблей.

Вариант 17.

1. На вход некоторого устройства подаётся переменное напряжение, амплитуда которого является стационарным и нормальным случайным процессом X(t) со среднимm_x= 5 и корреляционной функцией

K_x(τ) = 9e ^{–2 | τ |}(1 + 2| τ |). Найти среднюю длительность выброса амплитуды входного напряжения за уровень 8.

2. Случайный процесс Х(t) имеет корреляционную функцию K_x(τ) =

= σ²e ^–α|τ|[cos(ω₀τ) – (α/ω₀)sin(ω₀τ)] . Найти спектральную плотность этого процесса.

3. Пусть {ξ_n} – последовательность независимых случайных величин, имеющих одинаковую плотность распределенияp(x),p(x) > 0, – ∞ <x< ∞. Будет ли последовательность {η_n} марковской, если η_n= ξ_n,n = 0, 1, … .

4. В систему с одним обслуживающим аппаратом поступает простей-ший поток заявок с плотностью ν = 9,8 заявки в минуту. Число обслуженных заявок подчиняется закону Пуассона, причём среднее число обслуженных заявок в 1 мин.равно 10. Определить:

а) математическое ожидание длины очереди;

б) вероятности того, что в очереди находится 0, 1, 2 заявок;

в) вероятность того, что вновь поступившей заявке не придётся ждать;

г) среднее время ожидания.

Вариант 18.

1. Угол крена корабля θ(t) – стационарный и нормальный случайный процесс сM θ(t) = 0 и корреляционной функцией

, ([τ] =с).

Найти, сколько раз в среднем в течении 10 мин.угол крена будет равен 0.

2. Стационарный случайный процесс X(t) имеет корреляционную функциюK_x(τ) = σ²e ^{–α | τ |}(1 +α|τ | +α²τ²/3). Найти спектральную плотность процесса.

3. Пусть {ξ_n} – последовательность независимых случайных величин, имеющих одинаковую плотность распределенияp(x),p(x) > 0, – ∞ <x< ∞. Будет ли марковской последовательность {η_n},где η_n= ξ₀+ ξ₁+…+ξ_n,n= 0,1,….

4. Пусть на некоторую систему обслуживания поступают требования так, что ξ(t) – число требований за времяt – образует однородный марковский процесс со счётным числом состоянийω_i= 0, 1, 2, … . Из состоянияiсистема непосредственно может перейти только в состояние i + 1, i= 0, 1, 2, … . Таким образом, вероятности переходовp_i,i+1=α, остальные p_ij = 0 при i ≠j и, в силу марковского свойства, p_ii = –α. Используя прямую систему уравнений Колмогорова для переходных вероятностей получить систему уравнений для абсолютных вероятностей состоянийp_j(t) и, используя начальные условияp₀(0) = 1;p_i(0) = 0,i= 0, 1, 2, … , решить её, доказав при этом, что рассмотренный поток требований является пуассоновским.

Вариант 19.

1. Среднее число выбросов стационарного и нормального случайного процесса X(t) за нулевой уровень (то есть за средний уровеньa=m_x) в единицу времени равно 0,01. Дисперсия процессаX(t) равна 64. Найти дисперсию скорости изменения этого процесса, т.е. процессаV(t) = .

2. Стационарный случайный процесс X(t) имеет корреляционную функциюK_x(τ) = Aexp(–α²τ²). Найти взаимную спектральную плотностьS_xy(ω), еслиY(t) =dX(t)/dt, и взаимную корреляционную функциюK_xy(τ).

3. Пусть {ξ_n} – последовательность независимых случайных величин, имеющих одинаковую плотность распределенияp(x),p(x) > 0, – ∞ <x< ∞. Будет ли последовательность {η_n} марковской, если η_n=max{0, ξ₀, ξ₁, …, ξ_n}.

4. Рассмотрим систему M|GI|1|∞. Пусть после окончания обслуживания каждого требования с вероятностьюpоно покидает систему и с вероят-ностью 1 –p возвращается в очередь для повторного обслуживания независимо от остальных требований и числа предыдущих поступлений на прибор данного требования. Найти функцию распределенияF(x) интервалов времени между выходящими из системы требованиями в стационарном режиме.

Вариант 20.

1. Дифференцируемый случайный процесс X(t) имеет корреляционную функциюK_x(t, t*) = K_x(τ) = σ²exp(–ατ²). Найти математическое ожидание, дисперсию и корреляционную функцию процессаY(t) =X(t) +d X(t)/dt

2. Стационарный случайный процесс X(t) имеет корреляционную функциюK_x(τ) = e ^{– α| τ |}cosβτ, α,β > 0. Найти спектральную плотность процессаX(t) и время корреляции. Для получения последнего результата использовать приближение α <<β(при этомω–β ~ α).

3. Случайная величина ξ принимает лишь значения –1, 0, 1. Свои значения величина ξ может лишь в моменты t₁, t₂, …, t_k, …, причём процесс смены состояний описывается простой однородной цепью Маркова с матрицей переходных вероятностей . В начальный момент времениt₀ случайная величина ξ могла иметь любое из своих возможных значений с равными вероятностями.

а). Вычислить математическое ожидание Mξ через четыре шага (т. е. в момент времени t₄).

б). Является ли эта цепь регулярной (эргодичной)?

в). Найти предельные (финальные) вероятности и предельное матема-тическое ожидание.

4. Рассмотрим систему M |GI|1|∞. Пусть λ – интенсивность входящего потока; B(x) – функция распределения времени обслуживания. Найти функцию распределения интервалов времени между уходом из системы требований в стационарном режиме.

Вариант 21.

1. Траектория движения космического летательного аппарата в вертикальной плоскости задаётся двумя уравнениями:

X(t) = At² + Bt + C, Y(t) = Et² + Ft + H.

Коэффициенты A, B, C, E, F, H являются случайными, так как определяются из опыта с ошибками; их номинальные значения равныa,b, …,hсоответственно, а ошибкиΔA, ΔB, …,ΔH представляют собой случайные величины с равными нулю математическими ожиданиями и дисперсиямиD_A,D_B, …,D_H. Нормированная корреляционная матрица этих ошибок имеет вид

.

Определить математическое ожидание, корреляционную функцию и дисперсию случайных функций V(t), U(t), представляющих собой горизон-тальную и вертикальную составляющие скорости аппарата.

2. Показать, что не существует никакой стационарной случайной функции X(t), корреляционная функция которойk_x(τ) постоянна в каком-то интервале (–τ₁,τ₁) и равна нулю вне его.

3. Цепь Маркова управляется матрицей переходных вероятностей .

Классифицировать все состояния этой цепи. Будет ли цепь эргодична? Найти асимптотическое поведение p_{i j} (n) приn → ∞.

4. Простейший поток с интенсивностью λ, подающийся на вход некото-рой СМО, разрежается посредством следующего p– преобразования: каждое событие вероятностьюp остаётся в потоке и с вероятностьюq= 1 –p выбра-сывается. Доказать, что преобразованный поток также является простейшим и найти его параметр.

Вариант 22.

1. Рассматриваются две некоррелированные центрированные случайные функции X(t), Y(t) и их произведение Z(t) = X(t) Y(t). Доказать, что корреляционная функция произведения равна произведению корреляционных функций сомножителей:

K_z (t, t') = K_x (t, t') K_y (t, t').

2. На вход колебательного узла системы автоматического регулирования, передаточная функция которой имеет вид

подаётся стационарный белый шум, спектральная плотность которого равна S_x*(ω) =N. Определить дисперсию выходного сигнала.

3. Пусть {ξ_n} – цепь Маркова со значениями вZ⁺ с переходными вероятностями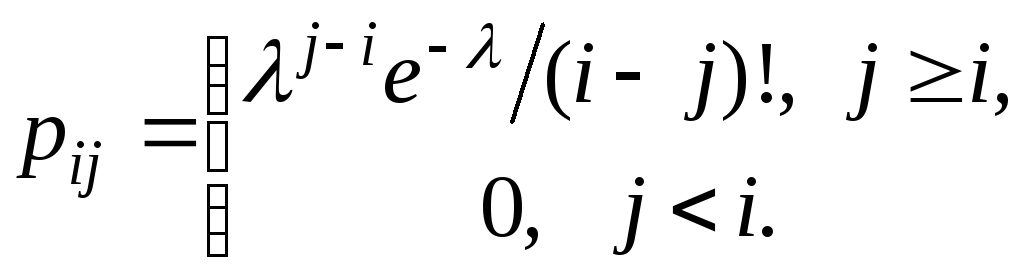Эргодична ли эта цепь и в случае положительного ответа найти финальные вероятности.

4. На автозаправочной станции имеется четыре заправочных колонки (n =4). Заправка одной машины длится в среднем 3 минуты. На автозаправку в среднем каждую минуту прибывает машина, нуждающаяся в заправке бензином. Число мест в очереди практически не ограничено. Все машины, вставшие в очередь на заправку, «терпеливо» дожидаются своей очереди. Определить среднее время, проходящее с момента прибытия машины на заправку, до момента её заправки, а также другие характеристики работы заправочной станции: среднее число занятых мест; среднее число машин в очереди; среднее время простоя колонки между заправками.

Вариант 23.

1. Пусть случайный процесс , где– независимые центрированные случайные процессы с корреляционными функциями. Найти корреляционную функцию процесса

2. Передаточная функция системы, на которую подаётся сигнал X(t), имеет видгдеk =25 (¹/c), T = 0,05 (c). Спектральная плотность входного сигнала, гдеT= 1(c), δ_x= 4 (град²/с²). Требуется найти дисперсию выходного сигнала.

3. Найти вероятности перехода p(x_k |t,x_j) ≡p_jk (t) для однородного поtмарковского процесса с дискретными состояниями, если постоянные коэф-фициентыA_jkдифференциальных уравнений для переходных вероятностей и/или вероятностей состояний процесса имеют значения:A_{j, j +1} =n₁,A_{j j} = – n₁,A_{j k} = 0 при остальныхk. Начальные условияp_jk (0) = δ_jk.

4. Стационарный поток Пальма, подающийся на вход некоторой СМО, разрежается посредством следующего p– преобразования: каждое событие вероятностьюp остаётся в потоке и с вероятностьюq= 1 –p выбрасывается. Доказать, что преобразованный поток также является потоком Пальма, и найти закон распределения и числовые характеристики промежутка между событиями в преобразованном потоке.

Вариант 24.

1. Случайная функция X(t) задана выражениемX(t) =V cosωt, гдеV– случайная величина с математическим ожиданиемm_v = 2 и среднеквадратичным отклонением σ_v= 3. Найти характеристики случайной функции: математическое ожиданиеm_x(t); корреляционную функциюK_x(t, t'); дисперсиюD_x(t). Определить, является ли случайная функцияX(t) стационарной. Найти характеристики случайной функцииY(t) =X(t) +αd(X(t))/dt, гдеα– не случайная величина. Является стационарной случайная функцияY(t)?

2. В радиотехнике для характеристики реализации на 0 ≤ t ≤ Tстационарного случайного процессаξ(t) с нулевым математическим ожиданием применяют так называемыйтекущий спектр .

Доказать, что спектральную плотность стационарного в широком смысле процесса ξ(t) с корреляционной функциейK(τ) при достаточно большихT(T → ∞) можно определить через текущий спектр:

.

3. Найти стационарные вероятности состояния P_k для однородного поtмарковского процесса с дискретными состояниями, если постоянные коэффициентыA_jk(j,k = 1, 2, …) дифференциальных уравнений для переходных вероятностей и/или вероятностей состояний процесса имеют значения:A_{j, j +1} =α,A_{j, j –1} =β>α,A_{j j} = –(α +β) приj> 1,A₁₁ = –α, A_{j k} = 0 при остальныхk.

4. Рассматривается предельный стационарный режим работы n-канальной системы массового обслуживания с отказами. Плотность потока заявокλ, плотность «потока обслуживаний» (потока освобождений одного занятого канала)μ. Требуется найти следующие характеристики СМО:

1) среднее число занятых каналов ;

2) вероятность занятости произвольно выбранного канала;

3) среднее время занятости одного (произвольно взятого) канала;

4) среднее время простоя канала .

Вариант 25.

1. Случайная функция X(t) имеет характеристики: математическое ожиданиеm_x(t) = 0; корреляционную функциюK_x(t, t') =. Найти характеристики случайной функцииY(t) =.

2. Пусть случайный процесс X(t) равен произведению двух стационарных в широком смысле некоррелированных процессовX₁(t) иX₂(t + τ₀):

X(t) =X₁(t)X₂(t + τ₀), гдеτ₀– фиксированная величина. Доказать, что спектральная плотность процессаX(t) будет определяться интегралом свёртки от спектральных плотностей процессов – сомножителей:

S(ω) =

3. Найти стационарные вероятности состояния P_k для однородного поtмарковского процесса с дискретными состояниями, если постоянные коэффициентыA_jk(j,k = 1, 2, …) дифференциальных уравнений для переходных вероятностей и/или вероятностей состояний процесса имеют значения:A_{j, j +1} =α,A_{j, j –1} = (j– 1)β,A_{j j} = –α – (j– 1)β, A_{j k} = 0 при остальныхk.

4. Рассматривается работа автоматической телефонной станции (АТС), рассчитанной на одновременное обслуживание 20 абонентов (двадцатиканальная СМО). Вызов на АТС поступает в среднем через 6 секунд. Каждый разговор длится в среднем 2 минуты. Если абонент застаёт АТС занятой, то он получает отказ. Если абонент застаёт свободным хотя бы один из 20 каналов, то он соединяется с нужным ему номером. Определить:

1) вероятность того, что абонент, вызывая АТС, не застанет её занятой;

2) среднее число занятых каналов ;

3) вероятность занятости канала;

4) среднее время простоя канала.

Вариант 26.

1. Имеются две случайные функции X(t) и Y(t) с характеристиками: математическими ожиданиямиm_x (t) =t², m_y (t) = 1 и корреляционными функциямиK_x (t,t') =exp{α₁(t + t')}, K_y (t,t') =exp{α₂(t'–t)²}. Найти характеристики случайной функцииZ(t) =X(t) +tY(t) +t²в двух случаях: случайные функцииX(t) и Y(t) –

а) некоррелированы, (взаимная корреляционная функция K_xy (t,t') = 0);

б) коррелированны, т. е. K_y (t,t') =aexp{ –α|t'–t |}.

2. Найти взаимную спектральную плотность процессов X(t) и X(t + t₀), гдеt₀– фиксировано иX(t) – стационарный случайный процесс с корреляционной функциейK_x (τ).

3. Флуктуации почернения фотоэмульсии.Пусть область эмульсии, соответствующая наименьшему различимому точечному объекту(коротко – ячейка), содержит в момент начала эксперимента (t= 0)N«непроявленных» зёрен. Каждое из них может находиться только в двух состояниях – непроявленном и проявленном. Если к моментуtостались непроявленнымиm зёрен (m = 1, 2, …,N), то предполагается, что вероятность проявления какого либо одного из них в в интервале (t, t + dt) равнаA_{m, m – 1}(t)dt = mα(t)dt, а вероятности проявления двух или более зёрен имеют более высокий порядок относительноdt.

4. Рассматривается система дозаправки самолётов горючим в воздухе. В районе дозаправки постоянно дежурят четыре самолёта – дозаправщика. Интенсивность полётов такова, что в среднем за час в район дозаправки пребывает 24 самолёта. Начавшаяся дозаправка осуществляется до конца и длится в среднем 10 минут. При занятости дозаправщиков, самолёт, нуждающийся в дозаправке, некоторое время «ожидает», совершая полёт по кругу (среднее время ожидания – 20 минут), а затем садится на запасной аэродром. Число самолётов, ожидающих дозаправки в воздухе, ничем не ограничено. Определить:

а) вероятность Р_обстого, что самолёт будет дозаправлен;

б) среднее число занятых дозаправщиков ;

в) вероятность занятости произвольно выбранного дозаправшика Р_обс;

г) среднее время простоя дозаправщика ;

д) среднее время «цикла работы» дозаправщика .

Вариант 27.

1. Процесс X(t) изменяет свои значения в случайные моменты времени. ЗначенияX(t) в промежутках между каждыми двумя скачками не изменяются и представляют собой независимые случайные величины с нулевым математическим ожиданием и одинаковой дисперсиейD. Найти математическое ожидание, дисперсию и корреляционную функцию этого процесса.

2. Случайные процессы X(t) и Y(t) стационарны и стационарно связаны, причём спектральные плотностиS_x (ω) иS_yx (ω) заданы. Найти взаимную спектральную плотность процессовU(t) =X(t) + Y(t)V(t) = , гдеt₀– постоянное.

3. Точка движется по плоскости и в течении секунды может сместиться или на единицу расстояния по горизонтали, или на единицу расстояния по вертикали, или пройти диагональ единичного квадрата (смещение на единицу расстояния по горизонтали и на единицу по вертикали) или остаться на месте. Вероятности горизонтального и вертикального смещений одинаковы и для любой секунды (кроме первой) равны: 1) α, если в предыдущую секунду произошли об смещения; 2)β, если в предыдущую секунду произошло только одно смещение по горизонтали или по вертикали; 3) γ, если в предыдущую секунду точка оставалась на месте.

Составить уравнение цепи Маркова для определения вероятностей горизонтального (вертикального) смещения точки в течении (n+ 1)-й секунды.

4. Рассматривается работа столовой самообслуживания. Обеды выдают четыре повара. Количество мест за столиками всегда достаточно мест для размещения лиц, уже получивших обед. Среднее время обслуживания (выдачи обеда) равно 4 мин.Плотность потока посетителей около двух человек в минуту. Условия работы столовой таковы, что в очереди могут одновременно стоять не более 20 человек. Посетитель стоит в очереди в среднем 10мин., после чего покидает столовую. На обед посетитель затрачивает в среднем 10мин.Определить:

а) среднее число занятых поваров;

б) вероятность того, что пришедший в столовую посетитель пообедает (вероятность обслуживания);

в) среднее число посетителей, ожидающих в очереди;

г) вероятность того, что все места в очереди будут заняты;

д) среднее время пребывания в очереди и среднее время, затрачиваемое на всю процедуру обеда.

Вариант 28.

1. Найти математическое ожидание и корреляционную функцию суммы двух некоррелированных случайных функций X(t) и Y(t) с характеристиками:

математическими ожиданиями m_x (t) =t, m_y (t) = –tи корреляционными функциямиK_x (t,t') =t t', K_y (t,t') =t t'exp{α(t'+t)}.

2. На вход динамической системы, которая описывается дифференциальным уравнением 5y'+y= 4x'+ 3x; (x = x (t); y = y (t)), подаётся стационарный случайный процессX(t) с математическим ожиданиемm_x= 3 и корреляционной функциейK_x(τ) = 2e ^{– α| τ |}. Найти математическое ожидание и дисперсию случайной функцииY(t) на выходе этой системы.

3. В урне находится 5 шаров, белые и чёрные. Последовательно проводятся испытания: каждый раз из урны случайным образом вынимается один шар и взамен него добавляют в урну шар другого цвета (если вынут белый шар – возвращается чёрный и наоборот). Доказать, что случайные величины ξ_n,n = 0, 1, 2, … удовлетворяют условиям однородной цепи Маркова. Найти:

а) матрицу вероятностей перехода за один шаг π(1);

б) матрицу вероятностей перехода за два шага π(2).

Эргодична ли эта цепь? При положительном ответе найти финальные вероятности.

4. Найти вероятность q_nтого, что в стационарном режиме в системеM|M |n |∞ все приборы заняты, если интенсивность входящего потока равнаλ, среднее время обслуживания –μ ^{– 1}, причёмλ<nμ.

Вариант 29.

1. Вычислить математическое ожидание и ковариационную функцию случайного фототелеграфного сигнала ξ(t), сформированного на основе пуассоновского потока упорядоченных временных точек {t_k ,k= 0, ±1, ±2, …} следующим образом: в интервалах между соседними точками ξ(t) есть постоянная величина, равная 1 или 0 с вероятностямиp и 1 – pсоответственно. Значения ξ(t) в разных интервалах независимы

2. На вход динамической системы, которая описывается дифференциальным уравнением 3y'+y= 2x'+ 3x; (x = x (t); y = y (t)), подаётся стационарный случайный процессX(t) с математическим ожиданиемm_x= 3 и корреляционной функциейK_x(τ) = 10e ^{– α| τ |}. Найти математическое ожидание и дисперсию случайной функцииY(t) на выходе этой системы.

3. Пусть ξ_t,t ≥0, – марковский случайный процесс со счётным множеством состояний {0, 1, …}. Предположим, что в момент времениt= 0 процесс находится в состоянииj. Найти функцию распределения времени до первого изменения состояния процесса.

4. Найти стационарные вероятности того, что в СМО типа M|M |n |m= =M|M |2 |10:

а) заняты все приборы (P_n);

б) заняты все места для ожидания (P_{n + m})

Вариант 30.

1. Вычислить математическое ожидание и ковариационную функцию случайного двоичного сигнала ξ(t), сформированного на основе простого пуассоновского потока упорядоченных временных точек {t_k ,k= 0, 1, 2, …} следующим образом ξ(t) = 1, если число точек в интервале (0,t) чётное, и ξ(t) = – 1, если число точек в интервале (0,t) нечётное.

2. На вход динамической системы, которая описывается дифференциальным уравнением y''+ 6y'+ 11y= 7x'+ 5x; (x = x (t); y = y (t)), подаётся стационарный случайный процессX(t) с математическим ожиданиемm_x= 11 и корреляционной функциейK_x(τ) = 2e ^{– | τ |}. Найти математическое ожидание и спектральную плотность процессаY(t) на выходе этой системы.

3. Показать для одношаговых случайных блужданий, у которых возможны смещения на один шаг вправо и влево (с вероятностями p и q), а также «шаг на месте» с вероятностьюp*, что в предположении существованиявероятности перехода за единицу времени A_jk (k ≠ j), причёмA_jj(t) = , уравнение Колмогорова для марковского случайного процесса с дискретным числом состояний выводится из уравнения Маркова.

4. Для системы массового обслуживания типа M|M |n |m=M|M |2 |10 найти:

а) математическое ожидание числа приборов, занятых обслуживанием в стационарном режиме;

б) математическое ожидание числа требований в очереди;

в) математическое ожидание числа требований в системе.