Задача 4.

1. Для системы массового обслуживания типа M |M |N |m =M |M |2 |10 найти:

а) математическое ожидание числа приборов, занятых обслуживанием в стационарном режиме ();

б) математическое ожидание числа требований в очереди ();

в) математическое ожидание числа требований в системе ().

Найти стационарные вероятности того, что в этой СМО:

г) заняты все приборы (P_N);

д) заняты все места для ожидания (P_{N + m}).

Рассчитать указанные характеристики при условии, что произведение интенсивности входящего потока λ и среднего времени обслуживания одной заявки 1/μ, т. е. величина ρ = λ/μ = 2

Р Е Ш Е Н И Е:

Данная СМО с N = 2-мя обслуживающими устройствами и m = 10-ю местами в очереди к ним характеризуется пуассоновскими входящим и выходящим потоками (т. е. экспоненциальным временем обслуживания заявок).

Так как данных о среднем времени ожидания заявок в очереди нет, полагаем систему с неограниченным временем ожидания (β = 0) и используя соответствующим образом модифицированные соотношения (3.3.24) – (3.3.31) (использование предназначенных для такого режима формул (3.3.32) – (3.3.35) невозможно, т. к. ρ = N) получаем:

а) = где P₀ =–

вероятность того, что все обслуживающие аппараты свободны. В данном случае имеем P₀ = 0,04 и математическое ожидание числа приборов, занятых обслуживанием в стационарном режиме = 1,84;

б) математическое ожидание числа требований в очереди

= = 1,84;

в) математическое ожидание числа требований в системе

= = 6,24;

г) вероятности того, что заняты все приборы P_N = =0,08;

д) вероятности того, что заняты все места для ожидания

P_{N + m} = = 0,08.

2. Обозначим через ν_t случайное число требований пуассоновского потока, поступивших в интервале [0, t). Доказать, что при t ≤ T, k ≤ n

P(ν_t = k | ν_T = n) = .

Р Е Ш Е Н И Е:

P(ν_t = k | ν_T = n) =

. Ч. т. д.

3. Найти вероятность P₀(t) свободного состояния в момент t системы

M|M|1|0, если интенсивность входящего потока равна λ, среднее время обслуживания – ¹/μ и:

а) в момент t =0 система была свободна;

б) в момент t =0 система была занята.

Р Е Ш Е Н И Е:

Свободное состояние системы в свою очередь можно разделить на два состояния: в систему не поступают новые заявки и не обрабатывается ранее поступившая заявка, либо новые заявки не поступают, но обрабатывается ранее поступившая. Это соответствует двум вариантам предлагаемых начальных условий: а) P₀(0) = 0; б) P₀(0) = 1. При составлении дифференциального уравнения, описывающего работу СМО, следует учитывать оба подсостояния, поэтому обозначим их вероятности P₀₀(t) и P₀₁(t).

Система дифференциальных уравнений для вероятностей состояний в этих случаях имеет вид: dP₀₀(t)/dt = – λP₀₀(t) + μP₀₁(t); dP₀₁(t)/dt = – μP₀₁(t) + +λP₀₀(t). Решая эту систему при заданных начальных условиях, получаем:

а) P₀(t) = P₀₀(t) = б) P₀(t) = P₀₁(t) =.

4. Рассмотрим систему M |GI|1|∞. Пусть после окончания обслуживания каждого требования с вероятностью p оно покидает систему и с вероятностью 1 – p возвращается в очередь для повторного обслуживания независимо от остальных требований и числа предыдущих поступлений на прибор данного требования. Найти функцию распределения F(x) интервалов времени между выходящими из системы требованиями в стационарном режиме.

Р Е Ш Е Н И Е:

Данная СМО имеет входящий пуассоновский поток с интенсивностью λ (заявок/сек) (для решения задачи необходимо задание этой величины) и произвольный закон распределение времени обслуживания заявок (обозначим эту функцию распределенияB(x), которая также необходима для решения задачи). Введём в рассмотрение величинуλβ₁< 1, имеющую смысл доли входного потока, поступившего на обслуживание; величинаβ₁=– имеет смысл средней длины интервала обслуживания. При заданных условиях и введённых обозначенияхфункция распределения F(x) интервалов времени между покидающими систему заявками (стационарный режим)

F(x) = (1 – p+ λβ₁) B(x) + (p – λβ₁) 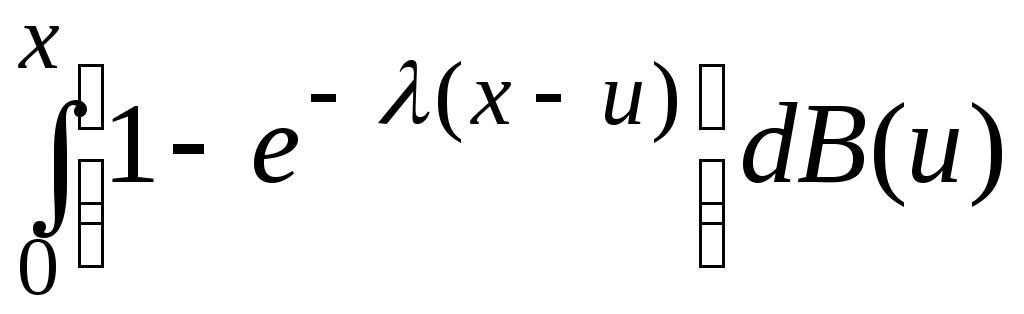. Если заявки покидают систему безвозвратно, следует положить в этой формулнеp =1. В приведённой формуле первое слагаемое отвечает за распределение времени обслуживания заявок, ещё находящихся в системе, а второе – задаёт распределение времени обслуживания заявок, покидающих систему.

Замечание: В данном случае требуемая формула не выводится (ввиду некоторых математических сложностей), а конструируется на интуитивных предположениях, но результирующая формула вполне может быть использована при решении других аналогичных задач.

5.На станцию текущего ремонта автомобилей поступает простейший поток заявок с плотностью λ = 0,5 машины в час. Имеется одно помещение для ремонта. Во дворе станции, ожидая очереди, могут одновременно находится не более трёх автомобилей. Среднее время ремонта одной машины τ_об =2 час. Определить:

а) пропускную способность этой системы автосервиса;

б) среднее время простоя станции;

в) как изменятся эти характеристики, если оборудовать второе помещение для ремонта (а если ещё и расширить площадку ожидания до 5 машин)?

Р Е Ш Е Н И Е:

Имеем: интенсивность простейшего входящего потокаλ=0,5; среднее время обслуживания заявок единственным приборомμ= 1/ τ_об = 0,5; максимальная длина очередиm = 3.

а). Так как ограничений на время ожидания в очереди нет, то вероятность того, что вновь прибывшая заявка покинет систему необслуженной в точности равна вероятности того, что заняты все места (и в очереди и на обслуживющих приборах), т. е. P_отк. = P_{N +m}, а последнюю находим по формуле (3.3.37):P_N+m=, гдеN= 1 (обслуживющий прибор),ρ=λ/μ= 1. ТогдаP_N+m= P₁₊₃= 1/5 =0,2.Относительнаяпропускная спосбностьсистемы при этомq= 1 –P_отк=0,8.Абсолютная пропускная спосбностьсистемыQ=λq=0,4машины в час.

б). Среднюю долю времени простоясистемы найдём по формуле (3.3.36) приk= 0, т. е. как вероятность того, что система свободна от заявок:

P₀= = 1/5 =0,2.

в). При N= 2;m =3 имеемP_отк=P₂₊₃ = (1/16)/(1+1+1/2+1/4+1/8+1/16) =

= 1/47 ≈ 0,021,q= 1 –P_отк≈0,979, т. е. удовлетворятся будет около 98 % всех заявок,Q=λq≈0,49 машин в час.Относительное время простоя P₀=

= 16/47 ≈ 0,34– оборудование будет полностью простаивать 34 % всего времени. При оборудовании ещё одной (такой же) площадки ожидания имеемN= 2,m =6. ТогдаP_отк=P₂₊₆ = (1/128)/(383/128) ≈0,00264,q= 1–P_отк≈0,9974

(практически все заявки будут удовлетворятся), Q=λq≈0,4999 машин в час, т. е. с полным использованием времени на ремонт,Относительное время простоя P₀= 127/383 ≈0,34– оборудование будет полностью простаивать 34 % всего времени. То, что простой оборудования при модернизации системы и её интенсификации практически не меняется говорит о том, чтоэта величина определяется соотношением интенсивностей поступления заявок и средним временем их обслуживания.

6. Рассматривается работа столовой самообслуживания. Обеды выдают четыре повара. Количество мест за столиками всегда достаточно мест для размещения лиц, уже получивших обед. Среднее время обслуживания (выдачи обеда) равно 4 мин. Плотность потока посетителей около двух человек в минуту. Условия работы столовой таковы, что в очереди могут одновременно стоять не более 20 человек. Посетитель стоит в очереди в среднем 10 мин., после чего покидает столовую. На обед посетитель затрачивает в среднем 10 мин. Определить:

а) среднее число занятых поваров;

б) вероятность того, что пришедший в столовую посетитель пообедает (вероятность обслуживания);

в) среднее число посетителей, ожидающих в очереди;

г) вероятность того, что все места в очереди будут заняты;

д) среднее время пребывания в очереди и среднее время, затрачиваемое на всю процедуру обеда.

Р Е Ш Е Н И Е:

Данная задача – пример работы СМО смешанного типа. Параметры этой системы таковы: число каналов обслуживания n = 4 (по числу поваров);

максимальное число мест в очереди m= 20;интесивность входящего потока(среднее число посетителе столовой)λ =2(1/мин.);среднее время обслуживание заявки(посетителя) 1/μ= 4(мин.) (время обслуживания одного, дождавшегося своей очереди, посетителя) (μ = 0,25 1/мин.);среднее время ожидания посетителя в очереди, после чего он покидает систему, 1/ν =10(мин.) (ν =0,1 1/мин.). Введём в рассмотрение также величиныρ=λ/ μ= 8; γ=λ/ ν= 20; δ =n μ/ν=γ/ρ= 10. Воспользовавшись обозначениями, которые приводятся в ПриложенииII, можно сразу записать:среднее число занятых каналов (поваров) (т. к.δ – целое число)

=≈3,99, т. е. практически все повара будут заняты.

Среднее число посетителей, ожидающих в очереди=

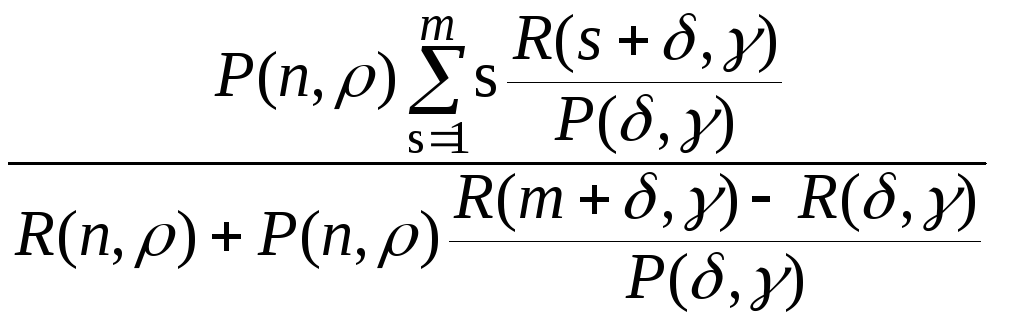= . Преобразуя сумму=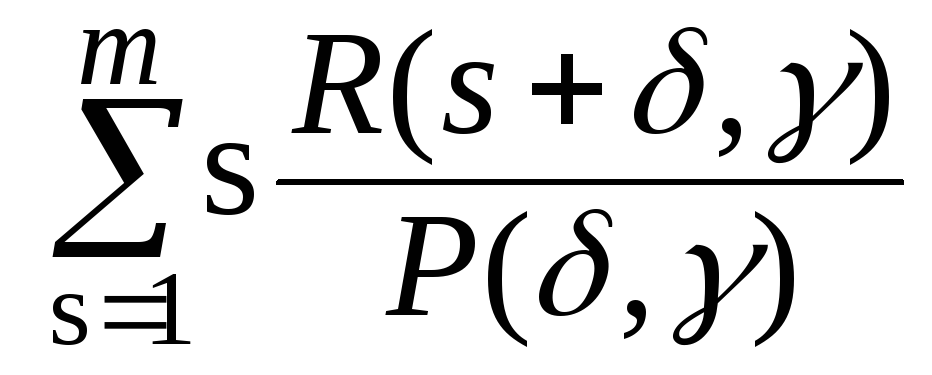

=

=, так как

=и. Следователо≈9,95.

Вероятность того, что все места в очереди будут заняты:

P_m=≈8,43 ·10^{– 3}, т. е. все места в очкреди будут заняты с вероятностью менее одного процента.

Вероятность обслуживания:P_обс =≈0,5.

Так как вероятность того, что все места в очереди будут заняты, мала, то сравнительно низкая вероятность обслуживания объясняется «нетерпеливостью» посетителей.

Среднее время пребывания в очереди: = 4,97≈5 (мин).

Среднее время, затрачиваемое на всю процедуру обеда:

T = = 4 + 10 + 5 = 19 (мин).

ПРИЛОЖЕНИЯ