Задача 3.

1. Простая однородная цепь Маркова с двумя состояниями управляется матрицей ,P₁ ≠ 0, P₂ ≠ 0. 1) Составить характеристическое уравнение и найти характеристические числа матрицы перехода. 2) Найти финальные вероятности P₁^ф и P₂^ф. 3) Сравнить стационарные (финальные) вероятности этой цепи для случаев: а) 0 ≠ P₁ ≠ P₂ ≠ 1; б) 0 ≠ P₁ = P₂ ≠ 1; в) 0 ≠ P₁ = 1 – P₂ ≠ 1. Частный случай P₁ или P₂ = 0 или 1 во всех этих случаях рассмотреть отдельно.

Р Е Ш Е Н И Е:

1). Прежде всего составим характеристическую уравнениеданной цепи Маркова, приравняв нулю её определитель: |λE - π| =

= (λ– 1)(λ+P₂–P₁) = 0. Решая это уравнение, найдёмхарактеристические числаматрицы перехода:λ₀= 1,λ₁= (P₁ –P₂); т. к. – 1 ≤ (P₁ –P₂) ≤ 1, то и –1 ≤λ₂≤ 1.

2). Так как все элементы матрицы переходов положительны, то цепь эргодична (положительно регулярна). Вычислим миноры определителя характеристической матрицы:P₁₁(λ) =λ–P₁;P₂₂(λ) =λ+P₂– 1. Тогда

, j= 1, 2;= .

3). В случае а) 0 ≤≠≤ 1, причём= 1/(1+P₂) и=P₂/(1+P₂) приP₁= 0,= 1 и= 0 приP₂= 0,= 0 и= 1 приP₁= 1 (P₂при этом может иметь любые значения; в случае б)= 1 –P₁,=P₂, что, в частности, даёт= 1 приP₁= 0 и= 0 приP₁= 1, а также= 0 или 1 приP₂ = 0 или 1; в случае в)= 1 и= 0 приP₁= 1–P₂= 0 и наоборот= 0 и= 1 приP₁= 1 –P₂= 1, а во всех других случаях== ½.

Замечание: Финальные вероятности можно найти и иначе. Найдём сначала матрицу π_n = π₁ⁿ перехода за n шагов. Для этого рассмотрим матрицу π₁ как матрицу линейного оператора А в эвклидовом пространстве R₂ с базисом f₁= и f₂=. Найдём собственные векторы оператора А: если имеем собственный вектор e =, то π₁e = λe, мы имеем систему Характеристический определитель = 0 даёт два собственных числа: λ₁ = 1 и λ₂ = p₁ – p₂. Собственные векторы имеют вид: e₁= и e₂= = . В базисе {e₁, e₂} матрица π₁* линейного оператора A диагональна: π₁*= , и поэтому π_n*= =. Остаётся вернуться к старому базису. ЕслиB – матрица перехода от базиса {e₁, e₂} к базису {f₁, f₂}, то π_n= B ^–1π_n*B. Пусть B =, тогда Be_j =f_j, j= 1, 2, т. е. α + β =1, γ + δ = 0 и α – βP₂/(1 – P₁) =0, γ – δP₂/(1 – P₁) = 1. Отсюда

B =. Так как det B = – (1 – P₁)/(1 – P₁ + P₂), то B ^–1= =; тогда π_n= . Так как (P₁ – P₂)ⁿ → 0 при n → ∞, то матрица стационарных переходных вероятностей имеет вид: π_∞ = , т. е. финальные вероятности=и= . ◊

2. На некотором острове погода бывает в течении дня или дождливой (Д) или сухой (С) т.е. представляет собой однородную цепь Маркова с двумя состояниями. Вероятности ежедневных изменений заданы матрицей

Д С

. а) Если в среду погода дождливая, то какова вероятность что она будет дождливой в ближайшую пятницу? б) Как изменится ответ на этот вопрос, если дождливая погода в среду ожидается с вероятностью 0,3?

Р Е Ш Е Н И Е:

а). Для того,чтобы ответить на вопрос: буде ли погода дождливой в ближайшую пятницу, если она дождлива в среду, необходимо рассчитать переходные вероятности заданной цепи Маркова за два шага. Такие вероятности задаются квадратом переходной матрицы: π²= π·π = =

= , т. е. вероятность дождя в пятницу равна0,61.

б). Вероятность того, что система, описываемая цепью Маркова, через n шагов попадёт в состояниеj, если в начальный момент она находилась в состоянииk, находится по формуле полной вероятностиp_j(t_n)= .

В данном случае, вероятности начальных состояний: p₁( 0) = 0,3 – дождливая погода в среду;p₂( 0) = 0,7 – сухая погода в среду, а вероятности перехода за два шага задаёт матрица π². Тогдаp₁(t₂) = 0,3·0,61 + 0,7·0,52 =0,547. ◊

3. Точка движется по плоскости и в течении секунды может сместиться или на единицу расстояния по горизонтали, или на единицу расстояния по вертикали, или пройти диагональ единичного квадрата (смещение на единицу расстояния по горизонтали и на единицу по вертикали) или остаться на месте. Вероятности горизонтального и вертикального смещений одинаковы и для любой секунды (кроме первой) равны: 1) α, если в предыдущую секунду произошли оба смещения; 2) β, если в предыдущую секунду произошло только одно смещение по горизонтали или по вертикали; 3) γ, если в предыдущую секунду точка оставалась на месте.

Составить уравнение цепи Маркова для определения вероятностей горизонтального (вертикального) смещения точки в течении (n + 1)-й секунды.

Р Е Ш Е Н И Е:

Пустьp_jгиp_jв – вероятности соответственно горизонтального и вертикального смещений на j –м шаге, тогдаp_{n+1, г} = p_{n+1, в} = p_{n, г}· p_{n, в}·α + p_{n, г}·

·(1 – p_{n, в})·β + p_{n, в}·(1 –p_{n, г})·β + (1 –p_{n, г})(1 –p_{n, в})·γ. Так какp_{n, г} = p_{n, в} = p_n,1 – вероятность смещения по одному какому-либо направлению, то

p_{n+1, 1} = p²_n,1α + 2 p_n,1(1 –p_n,1) β + (1 –p_n,1)²γ. ◊

4.Найти стационарные вероятности состояния P_k для однородного по t марковского процесса с дискретными состояниями, если постоянные коэффициенты A_jk (j, k = 1, 2, …) дифференциальных уравнений для переходных вероятностей и/или вероятностей состояний процесса имеют значения: A_{j, j +1} = α, A_{j, j –1} = β > α, A_{j j} = – (α + β) при j > 1, A₁₁ = – α, A_{j k} = 0 при остальных k.

Р Е Ш Е Н И Е:

Уравнение Колмогорова для такого марковского процесса имеет вид:

, а с учётом заданных обозначений получаем

то есть . Следовательно

, а с учётом условия нормировки вероятнстей состояния P_k следует, что . Окончательно . ◊

5. Пусть {ξ_n} – последовательность независимых случайных величин, имеющих одинаковую плотность распределения p(x), p(x) > 0, – ∞ < x < ∞. Положим S_t = S_k(t – k) + S_k+1(k + 1 – t), k ≤ t ≤ k + 1, S_n = ξ₁ + … + ξ_n. Будет ли процесс S_t марковским? Будет ли марковской последовательность {S_n}, n = 0,1,…

Р Е Ш Е Н И Е:

Нет, т. к. величины S_k и S_k+1, k =1, …, являются последовательными состояниями марковского процесса, при этом первое из них зависит от k – 1-го, а второе от k-го, то есть суммарный процесс S_t не удовлетвоояет марковскому свойству. Последовательность {S_n} в связи со сказанным выше является марковской последовательностью с непрерывным временем, то есть P(x, A) = ◊

6. Пусть ξ_t , t ≥ 0, – марковский случайный процесс со счётным множеством состояний {0, 1, …}. Предположим, что в момент времени t = 0 процесс находится в состоянии j. Найти функцию распределения времени до первого изменения состояния процесса.

Р Е Ш Е Н И Е:

Для однородных марковских процессов с конечным либо счётным числом состояний, справедливы прямая и обратная системы уравнений Колмогорова. Например 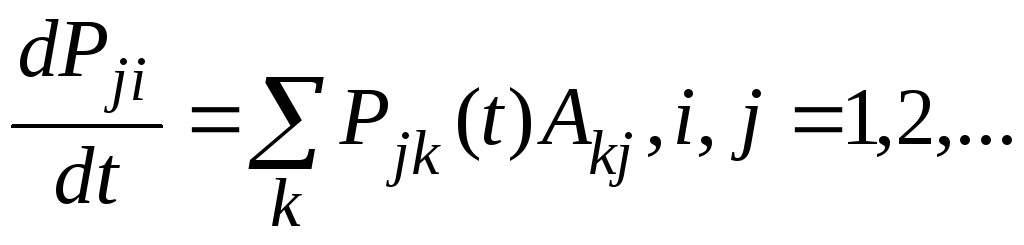, гдеA_kj . Находясь в конкретном состоянииj, процесс может сохранить это состояние, либо измиенить его, причём вероятности возможных изменений данного состояния определяются величинами A_kj. Обозначая λ_j = величину, имеющую смысл суммарной вероятности измененияj –го состояния процесса, легко перейти к уравнению для вероятности сохранения состояния (что соответствует распределению времени ожидания) , откудаP_jj(t) = 1– exp(– λ_jt). ◊

7. Цепь Маркова управляется матрицей переходных вероятностей .

Классифицировать все состояния этой цепи. Будет ли цепь эргодична? Найти асимптотическое поведение p_{i j} (n) при n → ∞.

Р Е Ш Е Н И Е:

Возводим матрицу во вторую, третью и т. д. степени. Очевидно π³ = π⁶ = … = π³ⁿ = т. е. цепь вполне разложима и цепь периодическая с периодом 3. Первое и второе состояния образуют первый изолированный цикл; 3-е и 4-е состояния также представляют собой ещё два цикла. Эргодичностью цепь не обладает, но при n = 3m и m → ∞ p₁₁(n) = p₁₂(n) = p₂₂(n) = p₂₁(n) = ½, p₃₃(n) = p₄₄(n) = 1, все остальные вероятности равны нулю. При n ≠ 3m и

n → ∞ p_ij(n) не имеют предела. ◊

8.Флуктуации почернения фотоэмульсии. Пусть область эмульсии, соответствующая наименьшему различимому точечному объекту(коротко – ячейка), содержит в момент начала эксперимента (t = 0) N «непроявленных» зёрен. Каждое из них может находиться только в двух состояниях – непроявленном и проявленном. Если к моменту t остались непроявленными m зёрен (m = 1, 2, …, N), то предполагается, что вероятность проявления какого либо одного из них в в интервале (t, t + dt) равна A_{m, m – 1}(t)dt = mα(t)dt, а вероятности проявления двух или более зёрен имеют более высокий порядок относительно dt.

Р Е Ш Е Н И Е:

При m непроявленных зёрнах в момент t возможен за последующий интервал dt либо переход к m – 1 непроявленным зёрнам с вероятностью mα(t)dt, либо сохранение числа непроявленных зёрен с вероятностью

1 – A_m,m(t)dt, причём A_m,m + A_{m,m – 1} = 0, т. е. A_m,m(t) = – mα(t). Следовательно, при m < N уравнение для p_m(t) будет d(p_m)/dt = [p_m(t)]'_t = A_m,m p_m + A_{m,m +1}p_{m +1} = – mα(t) p_m + (m +1)α(t) p_{m +1}, а при m = N, поскольку p_{N +1} = 0, =. Решение этих уравнений при начальном условии p_m(0) = δ_Nm даётся биномиальным законом p_m(t) =, гдеp(t) =

= e ^{– ρ(t)} , ρ(t) = . Очевидно, p(t) – вероятность того, что за время t зер-

но останется непроявленным. Таким образом, среднее значение и дисперсия m таковы: Процесс нестационарен и ] зависит от : , где =N– ––среднее число проявленных зёрен. С ростом N биномиальное распределение переходит (при фиксированном ) в пуассоновское. ◊

9. Показать для одношаговых случайных блужданий, у которых возможны смещения на один шаг вправо и влево (с вероятностями p и q), а также «шаг на месте» с вероятностью p*, что в предположении существования вероятности перехода за единицу времени A_jk (k ≠ j), причём A_jj(t) = , уравнение Колмогорова для марковского случайного процесса с дискретным числом состояний выводится из уравнения Маркова.

Р Е Ш Е Н И Е:

Уравнение Маркова для вероятности переходаp_n,mв данном случае имеет вид:p_{n +1, m} = p·p_{n, m – 1} + q· p_{n, m +1} + p*·p_{n, m} , p +q+p* = 1. Полагая

nΔt = t, перепишем это уравнение в видеp_m (t+Δt) = p·p_{m –1}(t) + q· p_m+1(t) + +p*·p_m (t). Если положить p = A_{m –1, m} Δt + o(Δt);q= A_{m +1, m} Δt + o(Δt);p* =1+ +A_{m, m} Δt + o(Δt), причёмA_{m, m} = – (A_{m –1, m} + A_{m +1, m}), то, разделив последнее уравнение наΔt, получаем, в пределе приΔt → 0,уравнение Колмогорова:

= A_{m –1, m} · p_{m –1}(t) + A_{m +1, m}· p_{m +1}(t) – (A_{m –1, m} + A_{m +1, m}) ·p_m (t). В частности, если блуждания симметричны, тоA_{m –1, m} = A_{m +1, m} и выбирая такой масштаб дляt, чтобы эти временные плотности вероятности были равны единице, получаем=p_{m –1}(t) + p_{m +1}(t) – 2 p_m(t). Подp_m(t) можно понимать каквероятность перехода p(t,ma|0,0) так ивероятность состояния

p(t, ma). ◊