5. Непрерывность, дифференцируемость и интегрируемость

случайных функций

Случайный процесс ξ(t) называется непрерывным в точке t₀, если , гдеl.i.m. означает «предел в среднем квадратичном», то есть это значит, что .

Замечание 1.5.1. Именно «в среднем квадратичном» следует понимать пределы в равенствах (1.4.13) – (1.4.15), определяющих характеристики эргодического процесса; пределы в этих соотношениях понимаются в обычном смысле, если случайный эргодичный процесс в них заменить любой его реализацией.

Теорема непрерывности: для непрерывности процесса ξ(t) (во всей об-ласти задания) необходима и достаточна непрерывность его математического ожидания m_ξ (t) в этой области и корреляционной функции K_ξ (t, t') на прямой t = t'.

Производной процесса ξ(t) называется процесс η(t), определяемый равенством

η(t) =. (1.5.1)

Это значит, что

.

Тогда справедливы следующие соотношения:

m_η (t) = (1.5.2)

K_η (t, t') =; (1.5.3)

D_η (t) =. (1.5.4)

Таким образом, можно сформулировать следующую теорему дифференцируемости: для дифференцируемости случайного процесса (в среднем квадратичном) во всей области задания необходима и достаточна дифференцируемость его математического ожидания m_ξ (t) в этой области и существование второй смешанной частной производной его корреляционной функции на прямой t = t'.

Пусть ξ(t) – случайный процесс, а g(t, s) – неслучайная функция двух переменных. Определённый интеграл по отрезку [0, T] процесса ξ(t) с весовой функцией g(t, s) определяется равенством

η(s) =. (1.5.5)

Очевидно, этот интеграл будет также некоторым случайным процессом η(s), зависящим от аргумента s.

Характеристики интеграла случайного процесса определяются следующими формулами:

• математическое ожидание

m_η (s) =(1.5.6)

• корреляционная функция

K_η (s, s') =; (1.5.7)

• дисперсия

D_η (s) = 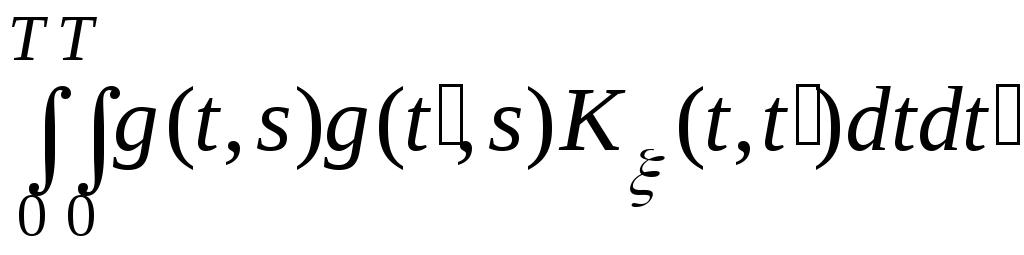. (1.5.8)

Аналогично, для интеграла с переменным верхним пределом (и весовой функцией, равной 1) имеем

η(t) =(1.5.9)

m_η (t) =(1.5.10)

K_η (t, t') =; (1.5.11)

D_η (s) =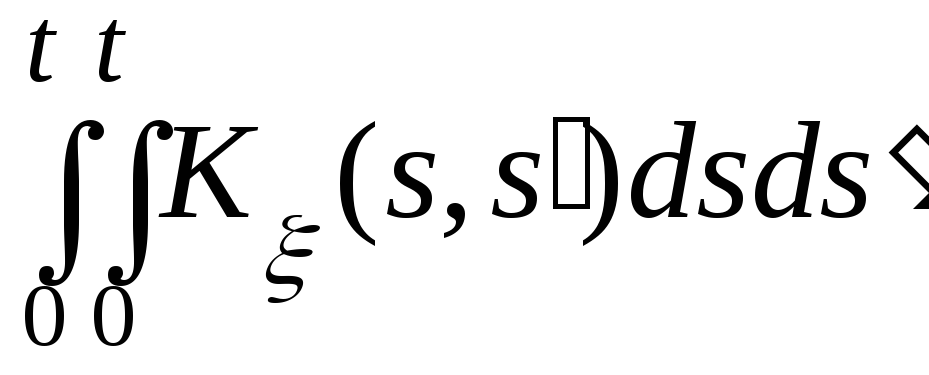. (1.5.12)

Для непрерывности стационарного процесса ξ(t) необходима и достаточна непрерывность его корреляционной функции K_ξ (τ) в точке τ = 0.

Для дифференцируемости стационарного процесса ξ(t) необходимо и достаточно существование K''_ξ (τ) в точке τ = 0, при этом

K_ξ' (τ) = – K''_ξ (τ). (1.5.13)

6. Спектральное представление случайных процессов и полей

Спектральная плотность случайного процесса

Каноническое разложение стационарной случайной функции имеет вид

ξ(t) = m_ξ (t) + , (1.6.1)

где постоянные ω_k > 0, U_k, V_k (k = 0, 1, …) – центрированные, некоррелированные случайные величины с попарно равными дисперсиями, т. е.

MU_k = MV_k = 0; M(U_kV_r) = M(V_kV_r) = M(U_kU_r) = 0,

(k ≠ r; k = r = 0, 1, …); D[U_k] = D[V_k] = D_k > 0. (1.6.2)

Разложение (1.6.1) называется спектральным, а точнее следовало бы сказать, что всякий процесс, представимый в виде разложения (1.6.1) есть стационарный процесс с дискретным спектром.

Корреляционная функция такого процесса также представима как сумма тригонометрического ряда с неотрицательными коэффициентами

K_ξ (τ) =, (1.6.3)

откуда, в силу (1.4.2), следует

D_ξ = K_ξ(0) = . (1.6.4)

Спектральное разложение (1.6.1) стационарной случайной функции при

ω₀ = 0 можно представить в виде комплексного ряда

ξ(t) = m_ξ (t) +, (1.6.5)

где

ω _{– k} = – ω _k , W₀= U₀ , W_k= (U_k – iV_k)/2, W_{– k}= (U_k + iV_k)/2 (k = 0, 1, …). (1.6.6)

Стационарные процессы, корреляционная функция которых не представима на всей оси τ в виде соотношения (1.6.3), называются процессами с непрерывным спектром. Для них корреляционная функция в наиболее важных случаях представима в виде интеграла Фурье

K_ξ (τ) =, (1.6.6)

где функция S_ξ (ω) ≥ 0 называется спектральной плотностью стационарного случайного процесса ξ(t).

Вообще говоря, спектральной плотностью стационарной случайной функции ξ(t) называется предел отношения дисперсии, приходящейся на данный интервал частот, к длине этого интервала, когда последняя стремится к нулю.

Спектральная плотность S_ξ (ω) и корреляционная функция K_ξ (τ) связаны преобразованием Фурье, то есть кроме прямого преобразования (1.6.6) справедливо и обратное

S_ξ (ω) =. (1.6.7)

Из соотношения (1.6.6) вытекает, что

D_ξ = K_ξ(0) =, (1.6.8)

то есть дисперсия («полная энергия») стационарного случайного процесса равна площади фигуры, ограниченной функцией спектральной плотности.

В комплексной форме преобразования Фурье, связывающие спектральная плотность S_ξ (ω) и корреляционная функция K_ξ (τ), имеют вид

; K_ξ (τ) =, (1.6.9)

где =S_ξ (ω)/2 – как так и S_ξ (ω) – действительные, неотрицательные чётные функции, но S_ξ (ω) рассматривается только на интервале (0, ∞).

Формулы (6 – 7) и (8 – 9) – равнозначны и носят название формул Винера – Хинчина.

Нормированной спектральной плотностью s_ξ (ω), называется спектральная плотность, делённая на дисперсию случайной функции

s_ξ (ω) = S_ξ (ω) / D_ξ ; =/D_ξ . (1.6.10)

Отметим, что нормированная спектральная плотность удовлетворяет тем же условиям, что и плотность вероятности:

S_ξ (ω) ≥ 0; . (1.6.11)

Учитывая, что нормированная корреляционная функция является Фурье-образом нормированной спектральной плотности

K_ξ (τ) =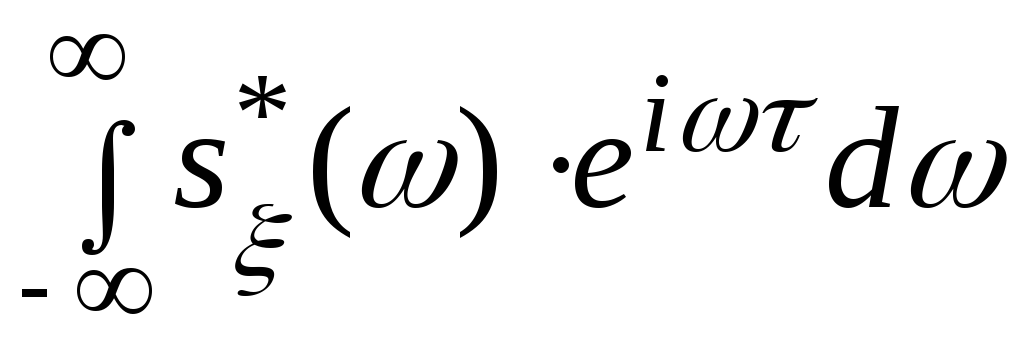, (1.6.12)

можно рассматривать нормированную спектральную плотность в качестве аналога плотности вероятности, а нормированную корреляционную функцию – в качестве аналога характеристической функции. Пользуясь подмеченной аналогией, можно ввести начальные и центральные моменты двусторонней и односторонней спектральной плотности.

Если ξ(t) и η(t) – два стационарно связанные между собой процесса с непрерывным спектром, то их взаимной спектральной плотностью называется преобразование Фурье их взаимной корреляционной функции связи:

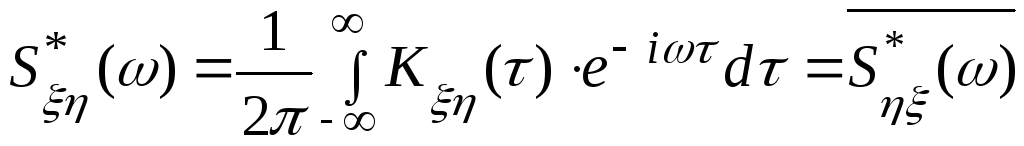; K_ξη (τ) =. (1.6.13)

Полагая τ = 0, получаем

= K_ξη (0) = M[ξ⁽⁰⁾(t)∙] =M{[ξ⁽(t) – m_ξ]∙[]}, (1.6.14)

чему можно придать наглядный физический смысл: если ξ(t) есть случайное напряжение на каком-либо элементе устройстве, а η(t) – случайный ток, протекающий через этот элемент, то величина K_ξη (0) равна средней мощности, выделяющейся на этом элементе.

Если процессы ξ(t) и η(t) ортогональны, т. е. взаимно некоррелированы, то K_ξη (0) = 0 и = 0 и наоборот. Тогда в соответствии с (1.2.38) имеем

S_{ξ +η} (ω) = S_ξ (ω) + S_η (ω), (1.6.15)

как для односторонних, так и для двухсторонних спектральных плотностей.

Следует также отметить, что в отличии от спектральной плотности одного случайного процесса, которая является действительной функцией частоты, взаимная спектральная плотность двух стационарно связанных процессов является обычно комплексной функцией частоты.

Поскольку для взаимной корреляционной функции справедливо неравенство | K_ξη (0) |² ≤ K_ξ (0) K_η (0), то и взаимная спектральная плотность при каждой частоте удовлетворяет неравенству |S_{ξ η} (ω)|² ≤ S_ξ (ω) S_η (ω).

Это неравенство позволяет для спектральных плотностей S_ξ (ω) и S_η (ω), отличных от нуля и не содержащих дельта-функций ввести в рассмотрение функцию частотной когерентности между процессами ξ(t) и η(t):

γ²_ξη(ω) = |S_{ξ η} (ω)|²/S_ξ (ω) S_η (ω), 0 ≤ γ²_ξη(ω) ≤ 1. (1.6.16)

Функция частотной когерентности аналогична квадрату нормированной взаимной корреляционной функции стационарно связанных процессов

R²_ξη(τ) = K²_{ξ η} (τ)/D_ξ D_η. (1.6.17)

Если процессы ξ(t) и η(t) некоррелированы, то функция когерентности равна нулю, а при линейной связи между процессами она равна единице.

Если η(t) =, то

S_η (ω) = S_ξ (ω) ω². (1.6.18)

Если процессы ξ(t) и η(t) связаны дифференциальным уравнением

,

где a_i и b_j – постоянные, то

Ф(i ω) = (1.6.19)

называется переходной функцией этого уравнения (точнее, линейной динамической системы, описываемой этим уравнением). Тогда

S_η (ω) = | Ф(i ω) |² S_ξ (ω), (1.6.20)

Причём это соотношение имеет место и в том случае, когда процесс ξ(t) не имеет производных вплоть до m – го порядка, но выполняется условие ограниченности спектра этого процесса

< ∞. (1.6.21)

Пусть стационарный в широком смысле процесс ξ(t) воздействует на вход линейной системы с постоянными параметрами, а процесс η(t) – процесс на выходе системы. Для стационарного состояния, когда справедлива формула (1.6.20), получаем γ²_ξη(ω) =.

Следовательно, функция частотной когерентности может принимать промежуточные значения между 0 и 1, когда процессы ξ(t) и η(t) связаны нелинейной зависимостью или когда выходной процесс η(t) определяется не только входным процессом ξ(t), но и какими-либо другими воздействиями. Для линейных систем величина [1 – γ²_ξη(ω)] служит мерой той части дисперсии процесса η(t), которая на частоте ω не зависит от входного процесса ξ(t).

Замечание 1.6.1. Нередко в технической литературе спектральную плотность вводят как Фурье-преобразование от ковариационной функции R(τ):

; R_ξ (τ) =, (1.6.22)

что не имеет принципиального значения, так как

S_ξ (ω) = S_0ξ (ω) + m_ξ² δ(ω), (1.6.23)

где δ(ω) = – дельта-функция (см. Приложение I). Таким образом, спектральная плотность стационарного процесса с неравным нулю математическим ожиданием отличается от спектральной плотности соответствующего центрированного процесса лишь наличием дискретной линии на нулевой частоте.

Замечание 1.6.2. Всё, сказанное выше о спектральной плотности, относится к случайным процессам, стационарным в широком смысле. Спектральную плотность S_ξ (ω) стационарного в узком смысле процесса ξ(t) можно выразить непосредственно через двумерную плотность вероятности f₂ (x₁, x₂; τ)

S_ξ (ω) =. (1.6.24)

Пары функций, представляющих собой преобразования Фурье друг для друга, обладают рядом характерных свойств, одно из которых количественно выражается в виде принципа или соотношения неопределённости. В частности, для корреляционной функции K(τ) и спектральной плотности S(ω) это выглядит так: чем «шире» спектр S(ω), тем «уже» корреляционная функция K(τ) и наоборот. Для количественного выражения этого принципа используем такие характеристики как «время корреляции» и «энергетическая ширина спектра», часто применяемые в различных технических задачах.

Под временем корреляции понимают величину τ_k , определяемую соотношением

, (1.6.25)

где r(τ) – нормированная корреляционная функция случайного процесса, определяемая соотношением (1.2.34).

Энергетическая ширина спектра Δω_э стационарной случайной функции определяется выражением

, (1.6.26)

где S_m = S(ω_m) – максимальное значение спектральной плотности, достигаемое в точке ω_m; иногда используют величину Δf_э = Δω_э /2π.

В этих терминах принцип неопределённости имеет вид:

τ_k ∙Δω_э ≥ 1/2 или τ_k ∙ Δf_э ≥ 1/(4π). (1.6.27)

Выбросом случайного процесса ξ(t) за уровень a называется событие

{ξ(t) > a}, а на практике, когда имеем дело с реализацией процесса X(t) – событие {X(t) > a}.

Для стационарного процесса с одномерной плотностью f (x) и плотностью двумерного вектора (ξ(t), dξ(t)/dt) = f₂(x, υ) (t – один и тот же момент), среднее время пребывания случайного процесса ξ(t) выше уровня a в течении времени T, среднее число выбросов за этот же промежуток времени за уровень a и средняя длительность одного такого выброса определяются формулами

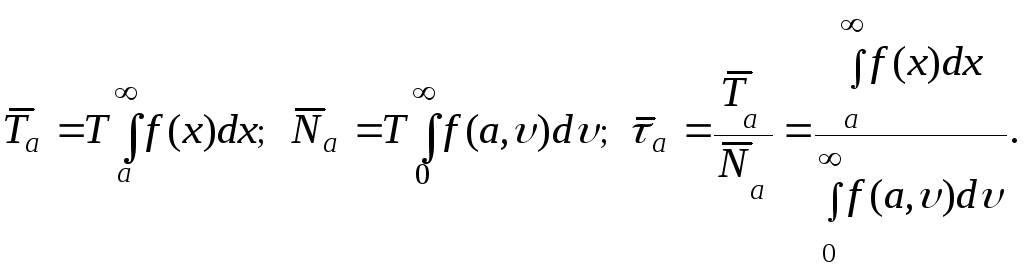(1.6.28)

Среднее число выбросов стационарного процесса в единицу времени .

Для стационарного и нормального процесса эти формулы имеют вид:

(1.6.29)

Замечание 1.6.3. (Ещё об эргодичности) В задачах практического определения спектральной плотности стационарного случайного процесса определения спектра в виде формул Винера – Хинчина (1.6.6 – 1.6.7) или (1.6.9) во многих случаях нельзя признать простыми и экономичными. Они предполагают предварительное определение корреляционной или ковариационной функции, что само по себе сопряжено с трудоёмкими вычислениями или измерениями, особенно для быстроосциллирующих корреляционных функций, которые часто встречаются в радиотехнике.

Представляются естественными два предположения: 1) попытка определить спектральную плотность по одной реализации достаточно большой длительности; 2) определение (измерение) спектральной плотности с помощью соответствующих спектроанализаторов, т. е. путём «пропускания» стационарного случайного процесса через частотно селективные устройства («спектральные окна») с последующим измерением нужных выходных величин.

Второе предложение реализуется, например, для случайных процессов в линейных системах, а первое оказывается неоправданным. Для реализации X(t), 0 ≤ t

≤ T, стационарного случайного процесса ξ(t) с нулевым математическим ожиданием (m_ξ = 0) текущий спектр (спектральную функцию)

F_T(iω) = , (1.6.30)

а также периодограмму, определяемую формулой

S_T(ω) = | F_T(iω) |²/T. (1.6.31)

Приведённые выражения носят формальный характер, так как и текущий спектр и периодограмма являются случайными функциями частоты: для разных реализаций одного и того же стационарного процесса ξ(t) конечной длительности T они изменяются от одной реализации к другой. Некоторый физический смысл и значение периодограмме придаёт следующее утверждение: если выполняется условие

(1.6.32)

то справедлива формула

S(ω) = . (1.6.33)

Таким образом, оценить спектральную функцию по одной реализации можно только для эргодической стационарной случайной величины.

Замечание 1.6.3. В отличие от спектрального анализа детерминированных сигналов (Фурье-анализ) спектральная плотность случайного процесса не даёт возможности восстановить какую-либо реализацию процесса, так как она есть осреднённая характеристика и не содержит сведений о фазах отдельных спектральных составляющих. Можно встретить различные по характеру случайные процессы, имеющие одинаковую спектральную плотность и корреляционную функцию. Поэтому эти две характеристики не вполне описывают случайный процесс.

Спектральный анализ детерминированных и случайных полей

В общем случае, если задано детерминированное поле ξ(r), где r – n-мерный вектор, то само поле и его спектральное представление S(k) представляют собой пару преобразований Фурье, имеющих вид:

S(k) = , (1.6.34)

ξ(r) = , (1.6.35)

где интегрирование ведётся по n-мерному объёму, k =(k₁, k₂, …, k_n ) – вектор волновых чисел; r = (x₁, …, x_n) – вектор n-мерного пространства; (k∙r) = k₁x₁ +

+ k₂x₂ + … + k_nx_n – скалярное произведение векторов.

В частности, если задано поле вида ξ(x, y, t), то его пространственно-временной спектр определяется выражением

Обратное преобразование Фурье в данном случае имеет вид

ξ(x, y, t) =

Отметим одно важное свойство многомерного преобразования Фурье. Если поле, например ξ(x, y, t), может быть представлено произведением

ξ(x, y, t) = ξ₁(x) ξ₂(y) ξ₃(t), (1.6.36)

то, в чём легко убедиться прямыми вычислениями,

S(k_x, k_y, ω) = S₁(k_x) S₂(k_y) S₃(ω). (1.6.37)

Справедливо и обратное утверждение.

Перейдём к определению спектральной плотности случайного поля. Пространственно-частотную спектральную плотность S(k) однородного случайного поля ξ(r) определим как преобразование Фурье от корреляционной функции K(Δr)

S(k) =, (1.6.38)

где k – вектор волновых чисел; (k∙Δr) – скалярное произведение векторов. Обратное преобразование Фурье в данном случае имеет следующий вид:

K(Δr) = , (1.6.39)

где K(Δr) – корреляционная функция однородного случайного поля. Из (1.6.39) непосредственно следует связь между дисперсией поля и его пространственной спектральной плотностью

D_ξ = K(0) =. (1.6.40)

Необходимо иметь в виду, что интегралы (как и вектора), входящие в написанные формулы, n-мерные.

В соотношениях (1.6.38), (1.6.39) можно заменить корреляционную функцию K(Δr) на ковариационную функцию R(Δr) при соответствующей замене спектральной плотности S(k) на спектральную плотность S₀(k), которые связаны соотношением (1.6.23).

По аналогии с одномерным спектром можно ввести эффективную ширину спектра Δk_э , определив её формулой

Δk_э =, (1.6.41)

где S_m – максимальное или какое-либо другое характерное значение спектральной плотности. Если для двумерного поля выполняется условие S(k_x, k_y) = S(k_x) S(k_y), то говорят об эффективной ширине спектра пространственных частот вдоль соответствующих координатных осей. Например

Δk_x =, Δk_y =.

Когда заданы два однородных и однородно связанных поля ξ(x, y) и

η(x, y) с известными взаимными корреляционными (ковариационными) функ-циями K_{ξ η} (Δx, Δy) и K_{η ξ} (Δx, Δy), то применение к последним преобразования Фурье даёт взаимные спектральные плотности

S_{ξ η} (k_x, k_y) = , (1.6.42.a)

S_{η ξ} (k_x, k_y) = .(1.6.42.b)

На основании обратного преобразования Фурье имеем

K_{ξ η} (Δx, Δy) =, (1.6.43.a)

K_{η ξ} (Δx, Δy) =. (1.6.43.b)

Так как взаимная корреляционная функция не обладает свойствами корреляционных функций инее обязательно должна быть чётной, то не всегда её можно представить в вещественной форме.