2. Описание случайных процессов и полей
Функция распределения и плотность вероятности
Одномерным законом распределения случайной функции ξ(t) называется закон распределения сечения X(t), т.е. t = t1 – фиксировано.
Одномерный закон распределения обычно задаётся одномерной функцией распределения
F1(x, t) ≡ F1(x1, t1) = P{ξ(t) < x} ≡ P{ξ(t1) < x1} (1.2.1)
(уровень функции x1 также фиксирован, хотя и произволен). Если функция F1(x1, t1) дифференцируема по x, то существует также одномерная плотность распределения
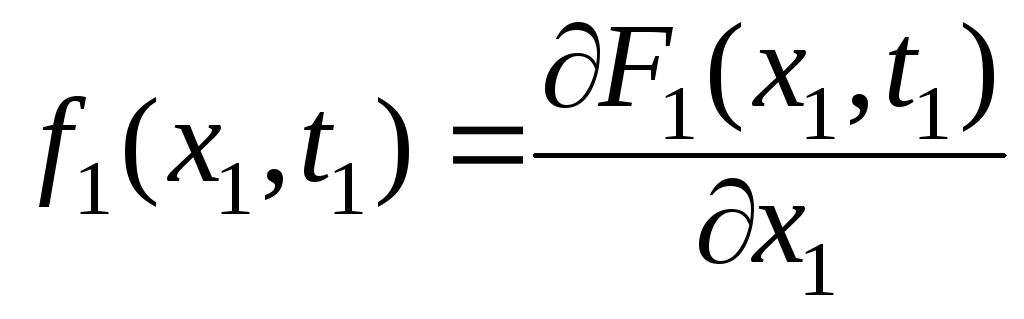. (1.2.2)
Для процессов с дискретными распределениями всех сечений этот одномерный закон распределения задаётся, как обычно, таблицей всех возможных значений данного сечения с их вероятностями:
{x1(t1), x2(t1), …, xn(t1), …}; { p1(t1), p2(t1), …, pn(t1), …},
pj(t1)
= P{ξ(t1)
= xj(t1)};
. (1.2.3)
Пусть t1, t2, …, tn – набор значений аргумента t. Образуем случайный вектор (X(t1), X(t2), …, X(tn)), компонентами которого являются сечения процесса ξ(t), соответствующие указанным значениям tj аргумента. Закон распределения этого n-мерного вектора называется n-мерным законом распределения процесса ξ(t). Обычно n-мерный закон распределения задаётся n-мерной функцией распределения
Fn(x1, …, xn; t1, …, tn) = P{X(t1) < x1, …, X(tn) < xn}, (1.2.4)
или n-мерной плотностью распределения
. (1.2.5)
Очевидно, n-мерная функция распределения и n-мерная плотность случайной функции ξ(t) зависят от n параметров – моментов t1, t2, …, tn . Для полной вероятностной характеристики произвольной случайной функции ξ(t)необходимо задание всех n-мерных законов распределения этой функции, т.е. для n = 1, 2,…, и при каждом n – для любого набора моментов t1, t2, …, tn. Для совместного вероятностного описания двух или нескольких случайных процессов вводят совместные функции распределения и плотности вероятности. Так для двух процессов ξ(t) и η(t) это имеет вид:
Fn +m(x1, …, xn, y1, …, ym; t1, …, tn, t'1, …, t'm) =
= P{ξ(t1) < x1, …, ξ(tn) < xn, η(t'1) < y1, …, η(t'm) < ym}; (1.2.6)
fn +m(x1, …, xn, y1, …, ym; t1, …, tn, t'1, …, t'm)dx1…dxn dy1…dym =
= P{x1 ≤ ξ(t1) < x1 + dx1, …, xn ≤ ξ(tn) < xn + dxn, y1 ≤ η(t'1) < y1 + d y1, …
…, ym ≤ η(t'm) < ym + dym}, (1.2.7)
где n и m – целые неотрицательные числа.
Определения функций распределения и плотностей вероятностей распространяются и на случайные поля. Пусть, например, имеется ансамбль реализаций скалярного поля ξ(x, y), полученный для момента t = t1. Так как в фиксированной точке пространства (x1, y1) значение функции ξ для разных реализаций есть случайная величина, то можно ввести одномерную функцию распределения случайного поля
F1(ξ1; x1, y1) = P{ξ(x1, y1) < ξ1}. (1.2.8)
Аналогично определяются 2, 3, …, n-мерная функция распределения:
Fn(ξ1, …, ξn; x1, y1; …; xn, yn) = P{ξ(x1, y1) < ξ1, …, ξ(xn, yn) < ξn} (1.2.9)
Если в формулах (8) и (9) функции F имеют частные производные по ξ, то можно определить соответствующие плотности вероятности:
f1(ξ1;
x1,
y1)
=
, (1.2.10)
fn(ξ1,
…, ξn;
x1,
y1;
…; xn,
yn)
=
. (1.2.11)
Отметим, что случайная функция называется нормальной, если закон распределения системы любого числа n её сечений представляет собой n-мерный нормальный закон распределения.
Для случайных процессов и полей можно ввести также условные плотности вероятности. Так, например, случайное значение процесса ξ(t1) при известном значении его в другой момент времени ξ(t2) = x2 описывается условной плотностью вероятности
f(x1; t1| x2; t2) = f2(x1, x2; t1, t2)/f1(x2; t2), (1.2.12)
где
f1(x2;
t2)
=
. (1.2.13)
Условная плотность вероятности f(x1; t1| x2; t2) содержит больше (по крайней мере не меньше) сведений о ξ(t1), чем безусловная плотность вероятности f1(x1; t1). Насколько именно увеличилась информация о f1(x2; t2) в результате того, что стало известным значение ξ(t2) = x2 зависит от конкретных условий. В некоторых случаях информации о ξ(t1) вообще не прибавляется, каким бы не оказалось значение x2. Это значит, что
f(x1; t1| x2; t2) = f1(x1; t1), (1.2.14)
при этом
f2(x1, x2; t1, t2) = f1(x1; t1) f1(x2; t2). (1.2.15)
Эта формула выражает необходимое и достаточное условие независимости значений случайного процесса ξ(t) в два момента времени t1 и t2.
Для физически реальных процессов, наблюдаемых в системах с конечной «памятью», равенства (14) и (15) выполняются в пределе при |t2 – t1| → ∞ почти всегда. В другом противоположном крайнем случае, когда разность (t2 – t1) → 0, физически очевидно, что для непрерывнозначных процессов
и,
следовательно
f2(x1, x2; t1, t2) = f1(x2; t2)δ(x1 – x2), (1.2.16)
где δ(x) – дельта-функция (см. Дополнение).
Характеристическая функция
Вместо функций распределения и плотностей вероятностей для описания случайного процесса можно использовать характеристическую функцию, связанную с указанными функциями преобразованием Фурье:
Фn(iθ1, …, iθn; t1, …, tn) = M{exp(iθ1ξ1 + … + iθn ξn)} =
=
(1.2.17)
=
(1.2.18)
Аналогично
для случайных полей. Так для случайного
поля
Фn(iθ1,
…, iθn;
,
…, 
)
= M{exp(iθ1ξ1
+ … +
iθn
ξn)}
=
(1.2.19)
Моментные и корреляционные (кумулянтные) функции;
математическое ожидание и ковариационная матрица
Различают начальные и центральные моментные функции.
Начальными
моментными функциями
случайного процесса ξ(t),
заданного на некотором (в общем случае
– бесконечном) интервале, называются
функции
симметричные относительно всех своих
аргументов, являющиеся математическими
ожиданиями соответствующих произведений:
,
,
. . . . . . . . . . (1.2.20)
Где
νj
(1≤ j
≤ n)
– неотрицательные целые числа. Момент
,
зависящий от n
несовпадающих аргументов t1,
…,tn
, называется n-мерным
моментом (ν1
+ ν2
+ … + νn)-го
порядка.
Кроме начальных рассматривают также центральные моментные функции, которые определяются формулой
.
(1.2.21)
Если моментные функции существуют, то их можно определить разложив характеристическую функцию в ряд Маклорена
Фn(iθ1,
…, iθn;
t1,
…, tn)
= M
(1.2.22)
где
,
. . . . . . . . .
.
(1.2.23)
В одномерном случае формула (23) приобретает вид
. (1.2.24)
Ковариационные (кумулянтные) функции R1(t); R2(t1, t2); R3(t1, t2, t3); …, определяются разложением в ряд Маклорена логарифма характеристической функции
ln{Фn(iθ1,
…, iθn;
t1,
…, tn)}
. (1.2.25)
Замечание 1.2.1. В аналогичном разложении логарифма характеристической функции в теории вероятностей коэффициенты, стоящие в нём, называют кумулянтами, откуда исходит второе название функций R.
В соответствии с (25) получаем
R1(t)
=
;R2(t1,
t2)
=
;
R3(t1,
t2,
t3)
=
.
(1.2.26)
Моментные и ковариационные функции связаны соотношениями:
m1(t) = R1(t); m11(t1, t2) = R2(t1, t2) + R1(t1) R1(t2);
m111(t1, t2, t3) = R3(t1, t2, t3) + R1(t1) R2(t2, t3) + R1(t2) R2(t1, t3) +
+R1(t3) R2(t1, t2) + R1(t1) R1(t2) R1(t3). (1.2.27)
Поскольку моментные и корреляционные функции определяются как коэффициенты разложения в ряд Макларена характеристической функции или её логарифма, т. е. функции и их производные рассматриваются в окрестности нуля (малого значения аргумента), то наиболее важными и существенными являются первые коэффициенты соответствующих разложений.
Весьма важную, можно сказать особую, роль играют математическое ожидание случайного процесса
mξ
(t)
= m1
(t)
= M
[ξ(t)]
=
, (1.2.28)
а также начальный момент m11(t1, t2), называемый ковариационной функцией случайного процесс
Rξ
(t1,
t2)
= m11(t1,
t2)
= M
[ξ(t1)
ξ(t2)]
=
(1.2.29)
и центральный момент μ11(t1, t2), называемый корреляционной (точнее, авто- корреляционной) функцией случайного процесса
μ11(t1, t2) = M {[ξ(t1) – mξ (t1)] [ξ(t2) – mξ (t2)]} =
=
. (1.2.30)
Очевидно, эти функции связаны соотношением
Kξ (t1, t2) = Rξ (t1, t2) – mξ (t1) mξ (t2). (1.2.31)
Изучение свойств случайных процессов, которые определяются лишь этими характеристиками, занимается раздел теории, называемый корреляционной теорией. Очень важный класс случайных процессов – гауссовские процессы, полностью описываются корреляционной теорией.
Для
случайного поля
моментные функции определяются как
интегралы от произведений значений
поля ξ1,
…, ξn
в заданных точках пространства на
соответствующую плотность вероятности.
Так, математическое ожидание равно
mξ
(
)
= m1
(
)
=
, (1.2.32)
а корреляционная функция
K(
,
)
= μ11(
,
)
= M
{[ξ1(
)
– m1
(
)]
[ξ2(
)
– m2
(
)]}
=
=
, (1.2.33)
где
интегрирование по векторам 
,
предполагает интегрирование по всем
полярным и азимутальным углам.
Также отправляясь от совместных и условных плотностей вероятностей, можно ввести совместные и условные моментные и корреляционные функции.
О с н о в н ы е с в о й с т в а к о р р е л я ц и о н н о й ф у н к ц и и.
1) Симметричность: Kξ (t, t') = Kξ (t', t).
2) | Kξ (t, t') | ≤ [Kξ (t, t) Kξ (t', t')]1/2 ≡ {D[ξ(t)] D[ξ(t')]}1/2 = σξ (t)σξ (t'), где D[ξ(t)] = σξ 2(t) = Kξ (t, t) – дисперсия процесса ξ(t).
3) Положительная определённость функции Kξ (t, t'), т. е.
,
гдеφ(t)
– любая комплекснозначная функция
(черта сверху означает комплексное
сопряжение); B
– произвольная область интегрирования.
Отметим также, что для нормальной случайной функции характеристики mξ (t), Kξ (t, t') являются исчерпывающими и определяют собой закон распределения любого числа сечений.
Случайная функция вида ξ0(t) = ξ(t) – mξ (t) называется центрированной случайной функцией, а вида ξ0н(t) = [ξ(t) – mξ (t)]/σξ (t) – нормированной случайной функцией.
Нормированной корреляционной функцией случайной функции ξ(t) называется коэффициент корреляции сечений X(t) и X(t')
. (1.2.34)
Очевидно, rξ (t, t') = 1 при t = t'.
Взаимной корреляционной функцией или корреляционной функцией связи двух случайных функций (процессов) ξ(t) и η(s) называется функция
Kξ η (t, s) = M [ξ0(t)·η0(s)] = M {[ξ(t) – mξ (t)]·[η(s) – mη (s)]}; (1.2.35)
Kξ η (t, s) = K η ξ (s, t). (1.2.35')
Если Kξ η (t, s) = 0, то говорят, что функции ξ(t) и η(s) некоррелированы. Пусть ζ(t) = ξ(t) + η(t); тогда
mζ (t) = mξ (t) + mη (t); (1.2.36)
Kζ (t, t') = Kξ (t, t') + Kη (t, t') + Kξ η (t, t') + Kξ η (t', t); (1.2.37)
D[ζ(t)] ≡ Dζ (t) = Dξ (t) + Dη (t) + 2 Kξ η (t, t). (1.2.37')
Если функции ξ(t) и η(s) некоррелированы, то
Kζ (t, t') = Kξ (t, t') + Kη (t, t') (1.2.38)
Dζ (t) = Dξ (t) + Dη (t) (1.2.38')
Если
ξ(t)
=
,
гдеξ1(t),
…, ξn(t)
– некоррелированные случайные функции,
то mξ
(t)
=
,Kξ
(t,
t')
=
.
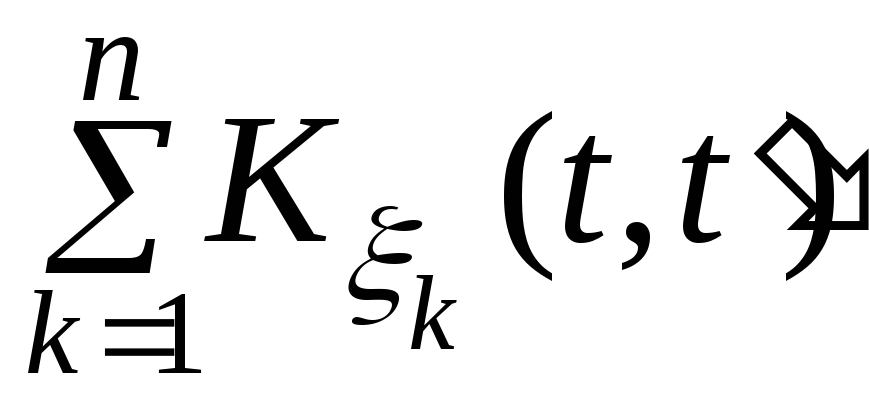