§ 7. Производная по направлению и градиент.

Рассмотрим функцию , определённую в некоторой окрестности точкии произвольный единичный вектор

L

y M

x

O x x+Δx

Для характеристики скорости изменения функции в точке в направлении векторавведем понятие производ- ной по направлению. Для этого через точкупроведём пря- муютак чтобы её направление совпадало с направлением ыектораи на направленной прямой выберем точку. Если- длина отрезка, то. При этом функцияполучает приращение.

Определение 1. Предел отношения при(, если он существует, называется производной функции в точкепо направлению вектора и обозначается

Если функция дифференцируема в точке , то её приращение вдоль прямой можно представить в виде:

где - бесконечно малые функции при. Разде –лим обе части последнего равенства на. Тогда, принимая во внимание, что, имеем:и при переходе в этом равенстве при, получаем формулу

(1)

Если же - функция трёх переменной, определён- ная в некоторой окрестности точки, а, где- углы, образованные век- тором с соответствующими осями координат - произвольный единичный вектор в пространстве, определяющий некоторое направление, производная функцииили, что то же самое, скалярного полявычисляется по формуле

(2)

ПРИМЕРЫ

1. Пусть . Найти про - изводную скалярного поляв точкев направлении вектора.Тогда, по формуле (1),

2. Найти в точкепроизводную скалярного поляв направлении вектора

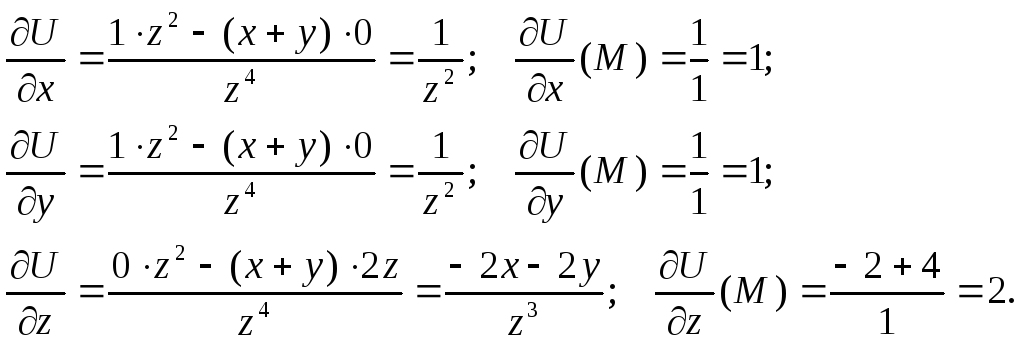
Тогда направляющие ко -синусы вектора :

Следовательно, по формуле (2)

Определение 2. Градиентом функции в точкеназывается вектор, координаты которого равны соответствующим частным производным.

Таким образом, (4)

Если вспомним формулу производной по направлению, получим

(5)

Но, по определению скалярного произведения, имеем

. (6)

Здесь - угол между вектороми единичным векто - ром направления. Из равенства (6) следует, что произ -водная функции по направлению имеет наибольшую величину при, т.е. когда направление вектора совпа -дает с направлением.

Замечание: Вектор показывает направление максимального изменения функции, а его длинаравна скорости максимального изменения.

Если функция трёх переменных и, то(7)

ПРИМЕРЫ:

1. Пусть . Найти, где.

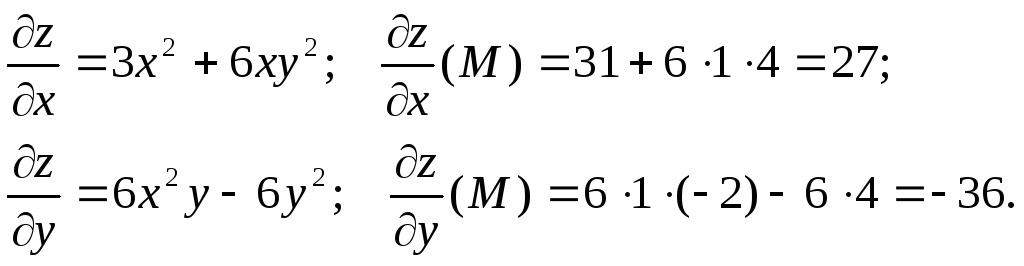
Тогда, ,по формуле (4),

3. Найти наибольшую скорость возрастания функции

в точке

Найдём .

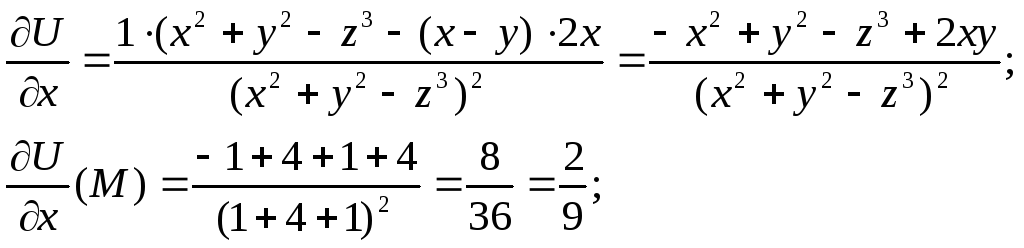
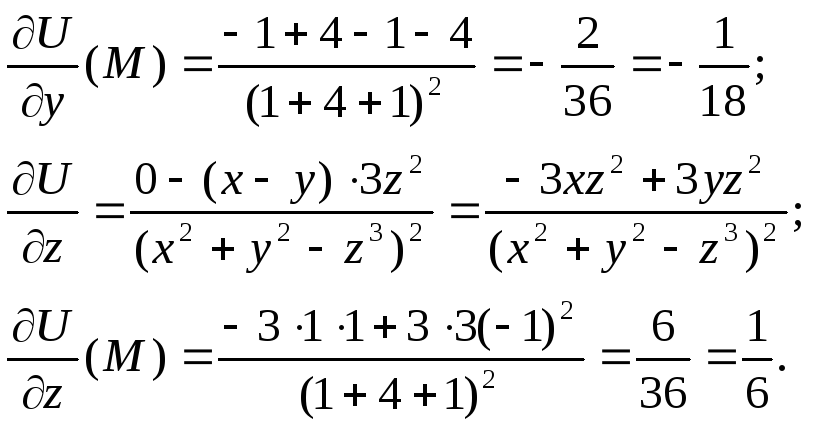
Тогда Его длина равна скорости наибольшего изменения функции

§ 8. Частные производные высших порядков.

Пусть в некоторой окрестности точки существуют частные производные функции:, которые сами являются функциями двух переменныхиНазовём их частнымипроизводными 1-го порядка.

Частные производные от этих функций по переменным и, если они существуют, называются частными производнымивторого порядка и обозначаются следующим образом:

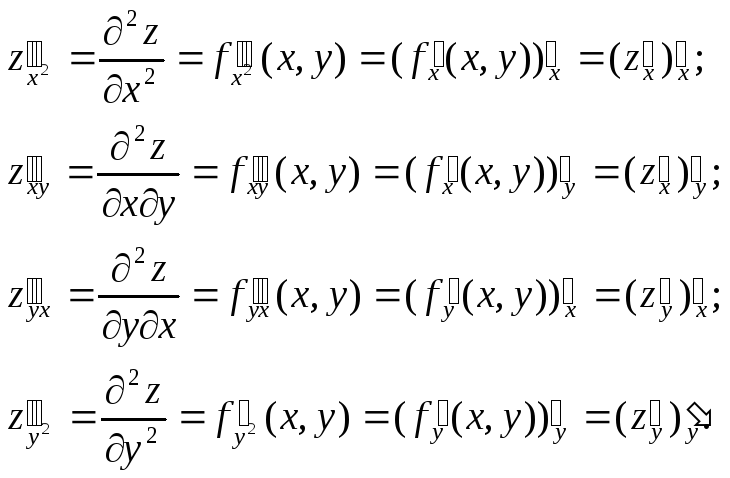
Частные производные называются сме- шанными частными производными. Для них имеет место сле -дующая теореме:

ТЕОРЕМА. Если производные сущест- вуют в некоторой- окрестности точкии непрерыв- ны в самой точке, то они равны между собой, т.е. имеет место равенство:.

Аналогичным образом можно ввести понятия частных про- изводных 3-го и более высоких порядков и частные произ -водные высших порядков для функция трёх и более пере -менных.

Теорема остаётся верной и для производных более высокого порядка. Например и т.д.

ПРИМЕРЫ:

1. Доказать равенство 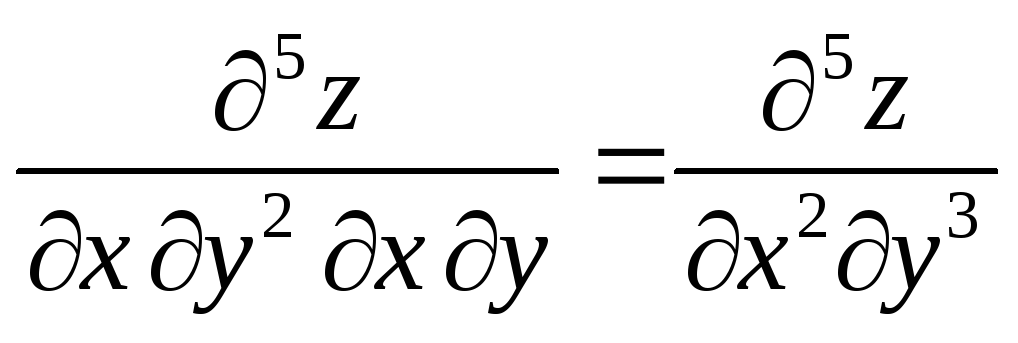для функции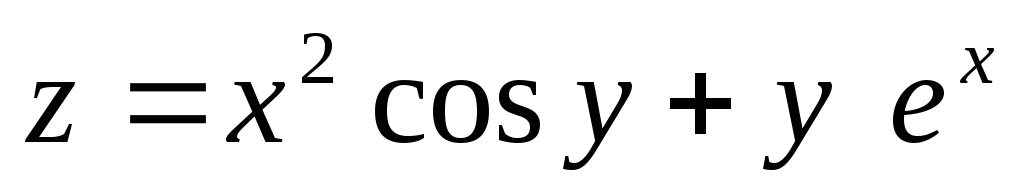

Таким образом, равенство доказано.

2. Пусть . Проверить, что выполняется равенство:

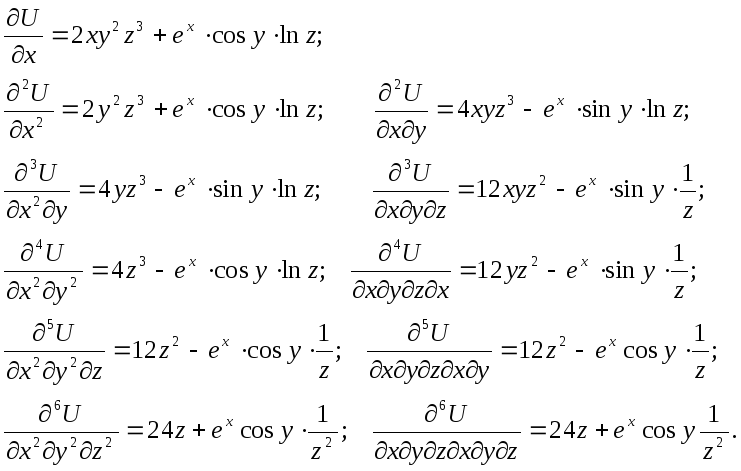Как видим, в этом случае равенство также выполняется.