§ 4. Несобственные интегралы.

Когда вводится определённый интеграл как предел инте -гральных сумм, обычно предполагается, что подынтегральная функция ограничена на отрезке и сам отрезок конечный. Если отказаться от этих условий, получим некоторые обобщения оп- ределённого интеграла, так называемые несобственные инте –гралы 1 – го и 2 – го рода.

1. Несобственный интеграл 1 го рода ( с бесконечными пределами интегрирования). Пусть функция опре -делена на промежуткеи интегрируема на любом конечном промежуткепри любом. Тогда, если существует конечный предел, то он называется несобственным интегралом 1 – го рода и обозначается

и интеграл при этом называется сходящимся; если же такой предел не существует или бесконечный, то интеграл называ- ется расходящимся.

Аналогично можно определить:

и

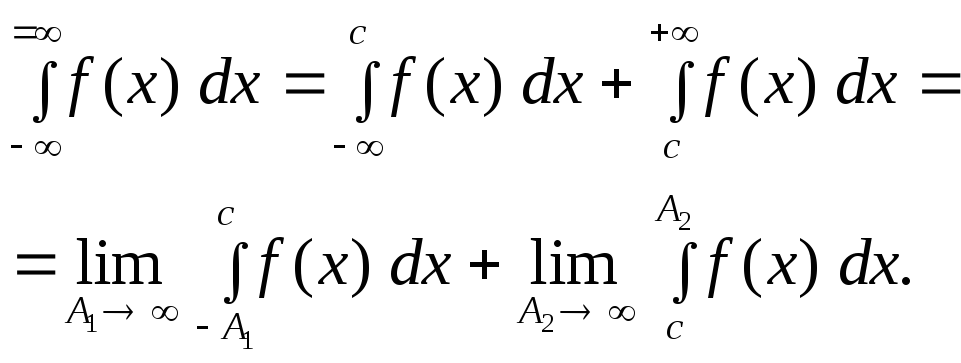
ПРИМЕРЫ:

1.

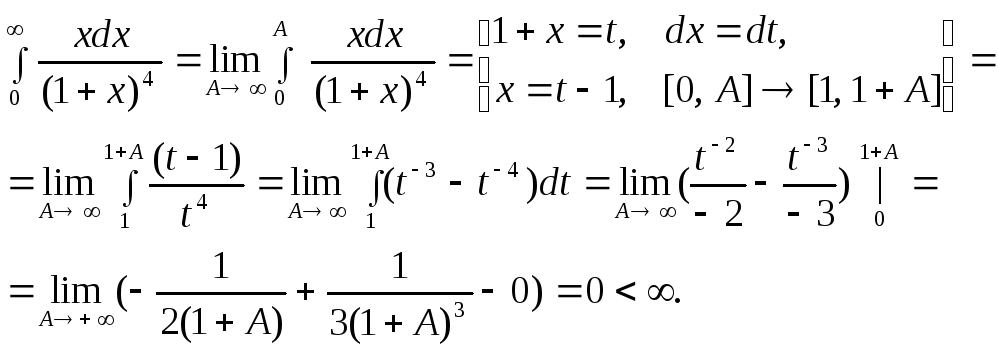
Следовательно, данный интеграл сходится.

2.

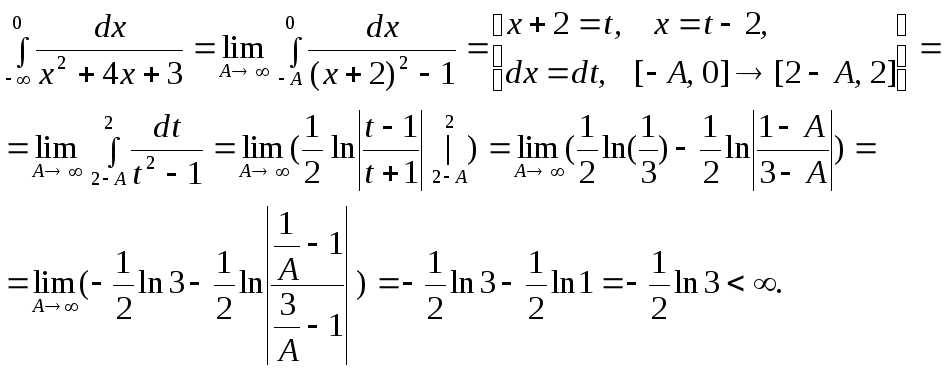Следовательно, интеграл сходится.

3.

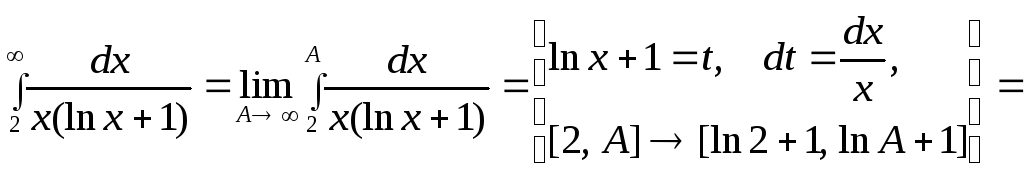
Следовательно, данный интеграл расходится.

2. Несобственный интеграл 2 – го рода (от неограни -ченных функций).

Пусть функция определена на отрезкеТочканазываетсяособой точкой, если функция неогра- ниченна в любой окрестности этой точки, но ограничена на любом отрезке . Если при любомсуществует определённый интеграли существует конечный предел притаких интегралов, то этот пре -дел называют несобственным интегралом 2 – го рода и обо- значают

Аналогично, если - особая точка, то

и, если особой точкой является некоторая точка , то

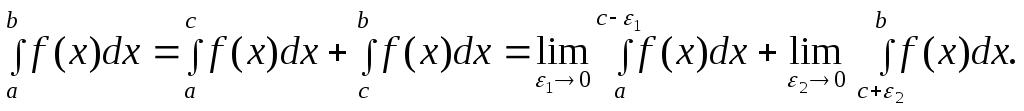
Если данные пределы существуют и конечны, то соответст -вующие интегралы 2 – го рода называются сходящимися. Если же данные пределы не существуют или бесконечны, то соот -ветствующие несобственные интегралы называются расходя – щимися..

ПРИМЕРЫ.

1.

(- особая точка )=

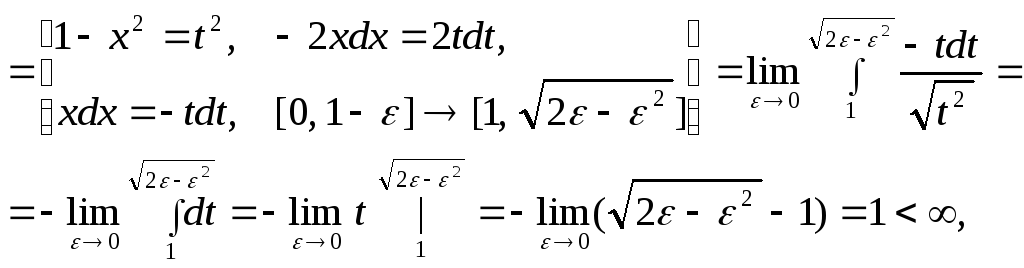
поэтому интеграл сходится.

2

Следовательно, данный несобственный интеграл расходится.

3. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.

§ 1 Основные понятия и определения

Определение 1. Пусть - некоторая область в плоскости. Если каждой точкеэтой области по опреде-лённому правилу соответствует вполне определённое значение величины, то говорят, что- этофункция двух независи -мых переменных (или аргументов) и, определённая в области . Символически это обозначается таким образом:

и т.д.

Как и функция одной переменной, функция двух перемен -ных существует не для всех значений своих аргументов.

Определение 2. Совокупность пар , при которых вы - ражениеимеет смысл,называется областью опреде -ления или областью существования функции .

Замечание. Аналогичным образом можно ввести понятие функции 3 – х и более переменных.

Например, если каждой точке трёхмерного про- странства по некоторому правилу ставится в соответствие не -которое действительное число, то говорят, что в простран- стве задана функция трёх переменныхи т.д.

ПРИМЕРЫ.

Найти области определения следующих функций:

Эта функция определена для множества точек плоскости, удовлетворяющих условиям:

.

Это кольцо, ограниченное окружностями радиусов 1 и 2, причём граничные окружности не входит в область опре -деления.

0 1 2

. Область определения этой функции определяется условиями:

Отсюда получаем эквивалентные условия:

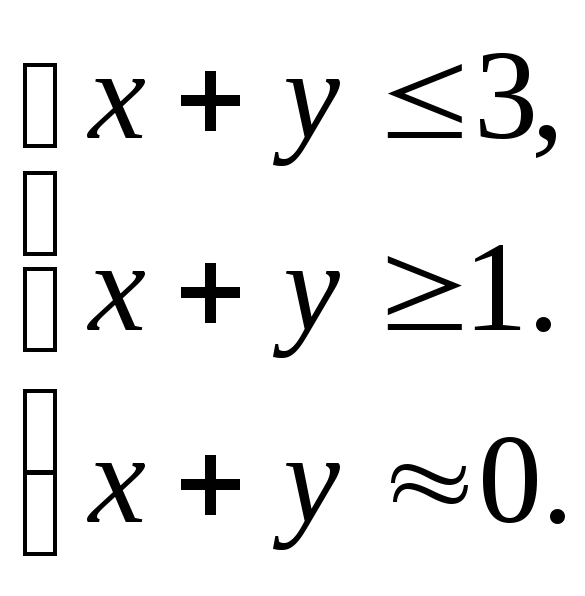
Третье условие, явно, является излишним. Получаем полосу:

0 1 2

Геометрическим изображением функции двух переменных является поверхность в трёхмерном пространстве, опреде -ляемая уравнением .