§ 5. Тройные интегралы.

Тройной интеграл является аналогом двойного интеграла, но вводится для функции трёх переменных и вместо плоской области областью интегрирования является пространст -венное тело.

Пусть в некоторой пространственной замкнутой ограни -ченной области определена ограниченная функция. Областьразбиваем напроизвольных частичных областей, не имеющих общих внутренних точек с объёмами. В каждой частичной области возьмём произвольную точкуи составим интегральную сумму. Пусть- максимальный диаметр частичных областей.

Определение. Если существует конечный предел этих интегральных сумм, то он называетсятройным интегралом от функции и обозначается следующим образом:

. (1)

Тройные интегралы являются обобщением двойных инте -гралом на случай трёхмерного пространства и, соответственно, обладают аналогичными свойствами.

Если предположить, что в области , то с помощью тройного интеграла можно вычислить объём области:

. (2)

ВЫЧИСЛЕНИЕ ТРОЙНЫХ ИНТЕГРАЛОВ

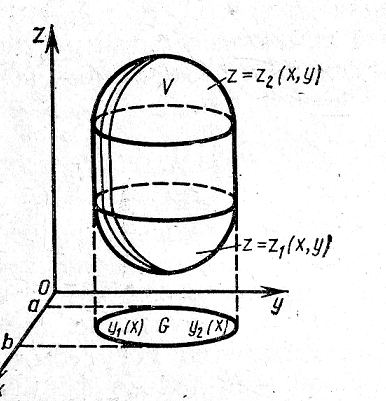
Пусть область представляет собой тело, ограниченное цилиндрической поверхностью, образующая которой парал -лельна оси, которое снизу и сверху ограничено поверх- ностямии. Пусть- проекция этого тела на плоскость. Пусть каждая прямая, параллельная оси, пересекает границу области не более чем в двух точках. Тогда для функции, непрерывной в области, вы- полняется формула:

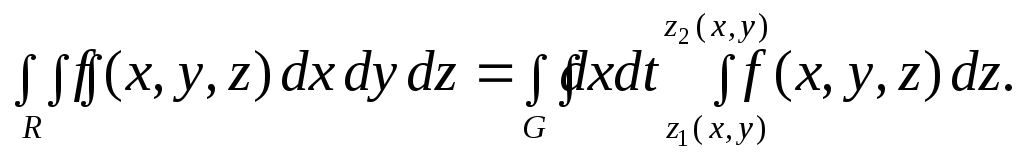(3)

Эта формула позволяет свести вычисление тройного интегра- ла к вычислению определённого и двойного интегралов. Если вспомнить формулу перехода от двойного интеграла к повтор- ному, то получим формулу:

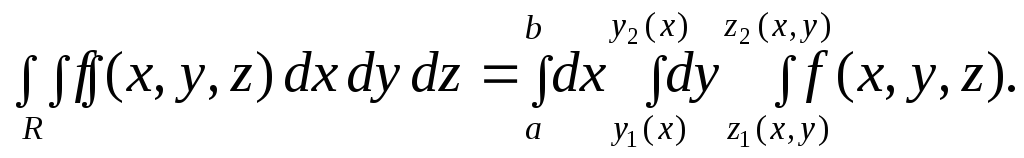
Таким образом, тройной интеграл можно вычислить после -довательно вычисляя три определённых интеграла.

ЗАМЕЧАНИЕ. При проектирование области на другую координатную плоскость мы получим другой порядок интегрирования.

ПРИМЕР. Вычислить , если областьограничена поверхностями:

Построим область в плоскости.

О 1

Этого рисунка достаточно для того, чтобы расставить пре -делы интегрирования, так как в этой области меняется от нуля до 0 до.

Тогда

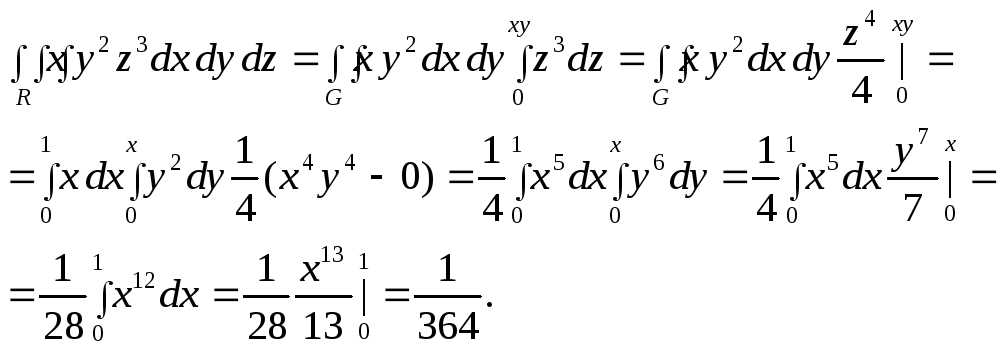
ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНОМ ИНТЕНРАЛЕ.

Если ограниченная замкнутая область пространствас помощью непрерывно дифференцируемых функций

взаимно однозначно переводится в область пространстваи якобиан

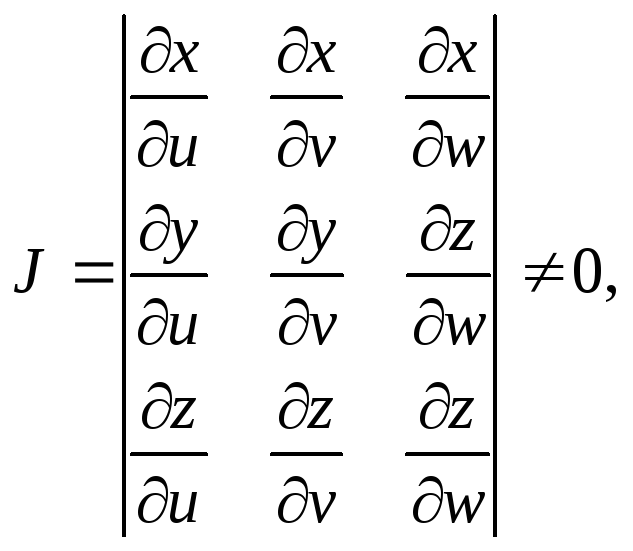
то можно применять формулу замены переменных в тройном интеграле:

Чаще всего эта формула применяется в случае перехода от декартовых координат к цилиндрическим коорди –натам(т.е. вводятся поляр -ные координаты на плоскости, аостаётся без изменения). В этом случае якобиан перехода такой же, как в случае пе -рехода к полярным координатам для двойного интеграла, т.е., и формула перехода к цилиндрическим координатам приобретает вид:

Переход к цилиндрическим координатам, обычно, приме –няется в случае, если область интегрирования представляет собой область, ограниченную следующими поверхностями:

Сфера, круговой цилиндр, параболоид вращения, круговой цилиндр и т.п.

ПРИМЕР. Вычислить тройной интеграл: , гдеобщая часть параболоидаи шара

2

2

Линия пересечения этих поверхностей представляет собой окружность, радиус которой определим, решив систему уравнений

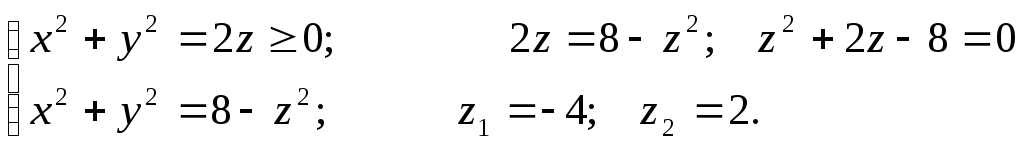
При радиус окружности равен 2. Т.е. в проекции на плоскостьмы имеем окружность радиуса 2, задаваемую уравнением. При переходе к цилиндрическим координата, так как, имеем, или. Таким образом, в нашей областименяется от 0 до 2,меняется от 0 до(полный круг),меняется от поверх -ности параболоидадо поверхности шара. Тогда, делая замену переменных в интеграле, получим:

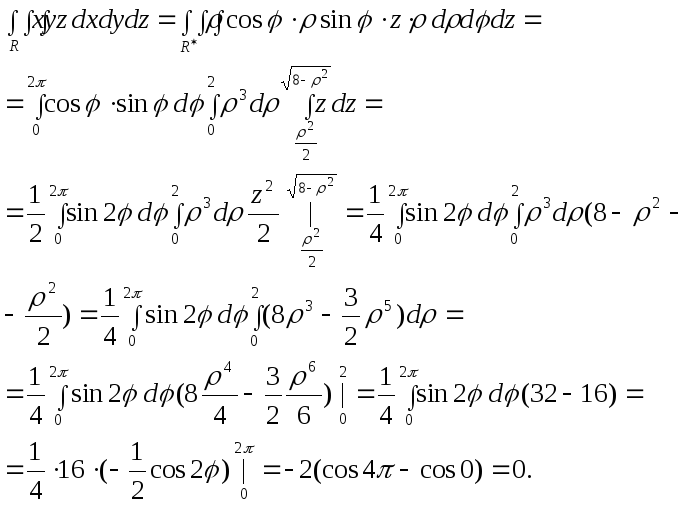
ПРИЛОЖЕНИЯ ТРОЙНЫХ ИНТЕГРАЛОВ.

Приложения тройных интегралов аналогичны соответствую –щим приложениям двойных интегралов.

1. Вычисление объёма тела:

ПРИМЕР. Найти объём тела, ограниченного следующими

поверхностями:

_ -

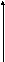
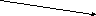
0

2

Проекцией этой области на плоскость является окружность

2

1 -

0

Поэтому целесообразно перейти к цилиндрическим коорди -натам. Уравнение этой окружности в полярных координатах имеет вид: , или. Конусв цилиндрических координатах имеет уравнение

. Тогда область

Объём находим по формуле

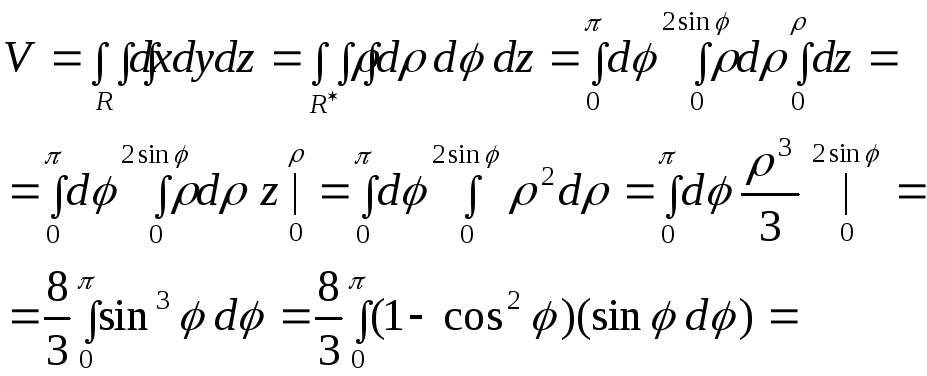
Замена

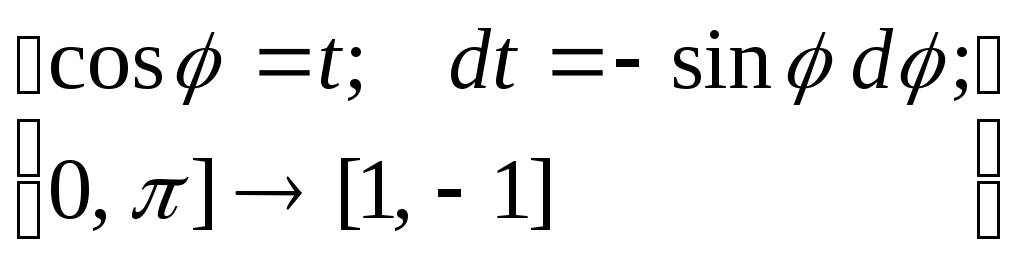
2. Вычисление массы тела.

. где - непрерывная функция, определяющая плот -ность тела в каждой точке области.

ПРИМЕР. Найти массу пирамиды, ограниченной плоскос- тями: если плотность в каждой точке равна абсциссе этой точки.

Решение.

Z

Y

3

2

-

0 3 y

0 2 x

2

x

Тогда, по формуле, масса равна

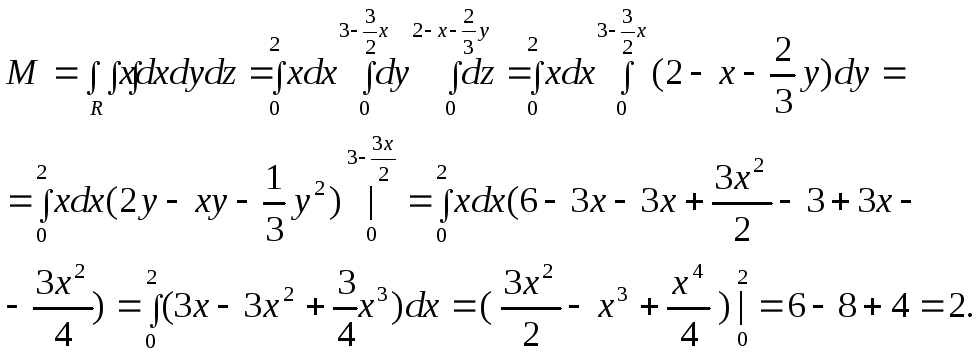
3. Вычисление моментов инерции тела с плотностьюпроизводится по формулам:

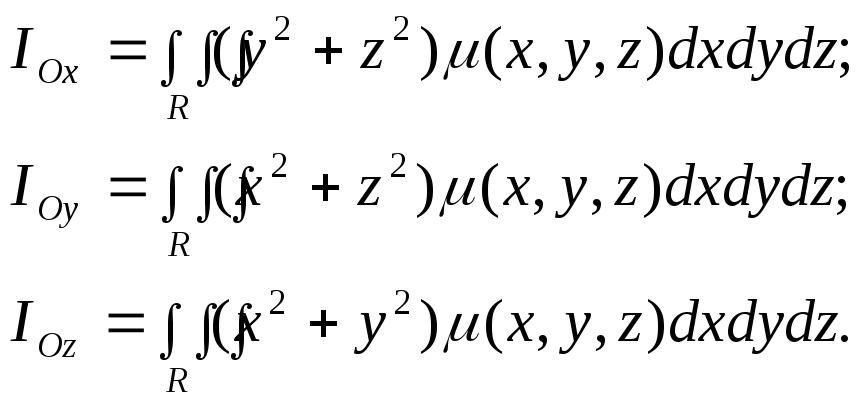
Момент инерции относительно начала координат находится по формуле:

4. Вычисление координат центра масс.

Координаты центра масс можно определить по следующим формулам:

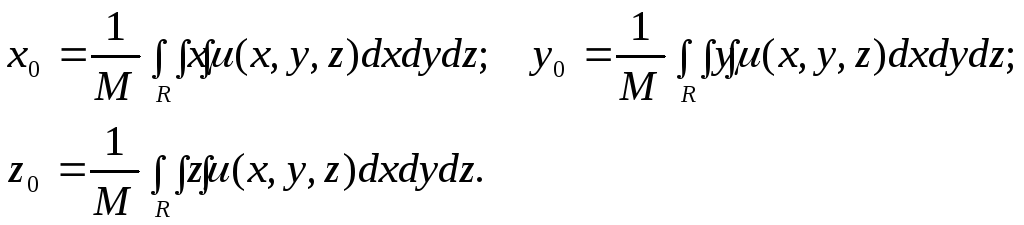
В частности, если тело однородное, то координаты центра масс определяются по формулам:

ПРИМЕР. Найти центр масс однородного тела, ограни -ченного поверхностями:

Решение.

0 4

Очевидно, что центр масс этого тела находится на оси , поэтому. Остаётся найти только. Снача- ла найдём объём этого тела. Область ориентирована вдоль оси, поэтому рассмотрим её проекцию на плоскость

0 2

Введём цилиндрические координаты следующим образом:

Тогда в области переменные меняются следующим образом:

Объём находим по формуле:

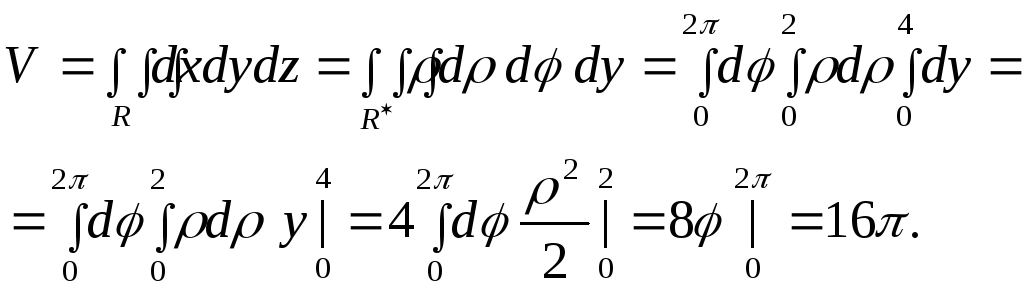
Тогда

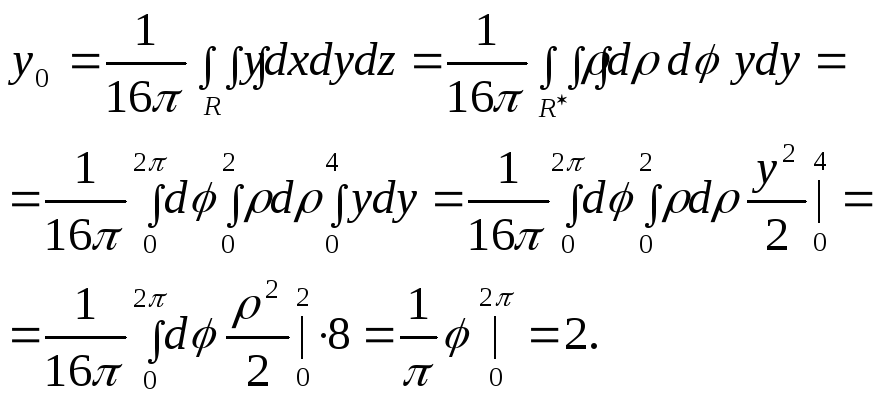
Таким образом, центр масс этого тела имеет координаты (0,2,0).