§ 3. Некоторые геометрические приложения определённого интеграла.

1. Площадь криволинейной трапеции. (из геометри- ческого смысла определённого интеграла):

(1)

ПРИМЕР 1. Найти площадь фигуры, ограниченной линиями: Это две параболы. Вершина первой в точке (1, 4), ветви направлены вниз; вершина второй в точке (2, -1), ветви направлены вверх.

4

3

1 2 3

О

-1

Площадь заштрихованной фигуры можно найти по формуле:

2. Найти площадь фигуры, ограниченной линиями:

2

-1 0 4

-1

Найдём точки пересечения линий

Площадь находим по формуле:

ЗАМЕЧАНИЕ Для вычисления площади криволинейной тра -пеции в случае, когда верхняя граница задана параметричес -кими уравнениями причём, то в формуле (1) необходимо сделать замену переменной, положив. Получим:

(2)

Например, найти площадь одной арки циклоиды:

2

О

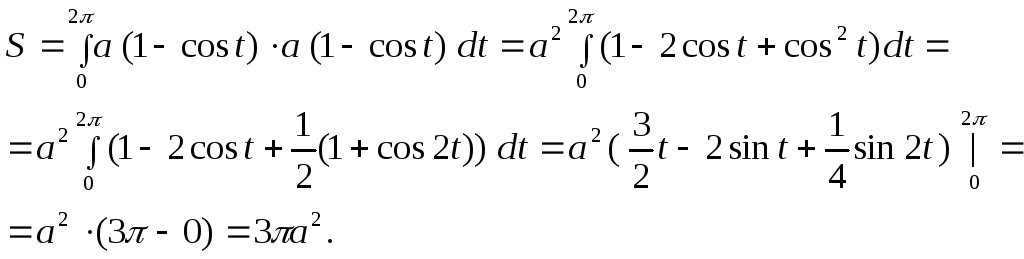
2. Площадь криволинейного сектора.

Пусть кривая в полярных координатах задана урав -нением, где функцияположи -тельна и непрерывна на отрезке. Фигуру, ограниченную двумя лучами, образующими с полярной осью углыи, и кривой, называют криволинейным сектором. Площадь криволинейного сектора ищется по формуле:

(3)

x

Например, Найти площадь кардиоиды .

y

a

2a 0 x

3. Длина дуги кривой.

а) Пусть плоская кривая задана уравнениемна отрезкегденепрерывна вместе со своей производнойна отрезкетогда длина дугивычисляется по формуле:

. (4)

ПРИМЕР. Найти длину кривой на отрезке

. По формуле (4),

ЗАМЕЧАНИЕ 1. В случае, если дуга задана парамет -рическими уравнениями; , причём , в формуле (4) можно сделать замену переменной:.

Получим:

или . (5)

ПРИМЕР: Найти длину дуги кривой, заданной параметри -ческими уравнениями:

Тогда

ЗАМЕЧАНИЕ 2. Для вычислении длины дуги в случае, ког- да кривая задана в полярных координатах уравнениемприменяется следующая формула:

(6)

ПРИМЕР: найти длину дуги кривой , если.

Тогда

4. Объём тела вращения.

Пусть функция непрерывна и неотрицательна на отрезке. Тогда объём тела, образованного вращением вокруг осикриволинейной трапеции, ограничен- ной сверху графиком функции, можно найти по формуле:

(7)

ПРИМЕР: Найти объём тела, образованного вращением вокруг оси фигур, ограниченных графиками функций:

y

1 x

Объём полученного тела находим следующим образом

Симметричная формула получается для вычисления объё -ма тела, образованного вращением некоторой фигуры вокруг оси

(8)

ПРИМЕР. Найти объём тела ,образованного вращением вокруг оси фигуры, ограниченной линиями

y

1 2

Найдём объём полученного тела. Найдём пересечение линий, ограничивающих область: при . Тогда,

. Если то. Тогда