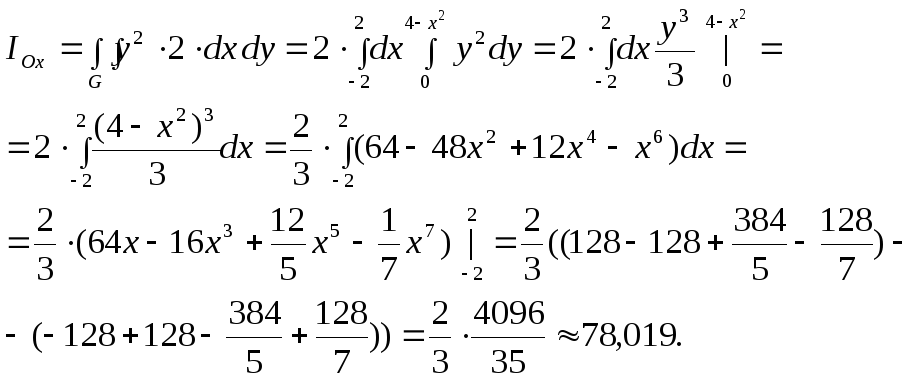§ 3. Замена переменных в двойном интеграле.

ПЕРЕХОД К ПОЛЯРНЫМ КООРДИНАТАМ.

Пусть непрерывна в некоторой замкнутой ограни- ченной области, Тогда для функциисуществует двойной интеграл. (1)

Пусть с помощью формул . (2)

мы переходим к новыми переменным, которые определяются из формул (2) единственным образом с помощью формул:

(3)

С помощью формул (3) каждой точке областиставится в соответствие единственная точкаобласти. Формулы (2) называютформулами преобразования коор- динат, а формулы (3) - формулами обратного преобразова -ния.

При сделанных предположениях, при условии, что функции (2) имеют в области непрерывные частные производные, если определитель

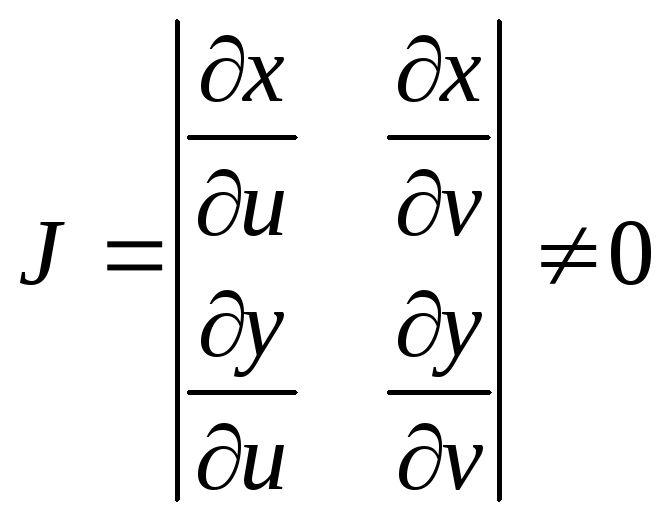(4)

для интеграла (1) имеет место формула

, (5)

Этот определитель называется функциональным определи -телем или якобианом. Чаще всего приходится формулу (5) применять при переходе к полярным координатам, в случае, ели область интегрирования определяется окружностями.

Полярные координаты вводятся равенствами:

. При данном преобразовании координат якобиан

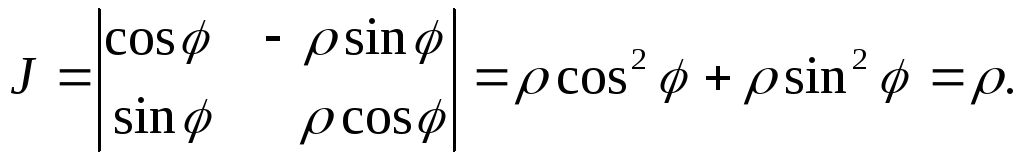
В этом случае получаем формулу перехода к полярным ко- ординатам:

(6) ПРИМЕР. Вычислить двойной интеграл , где областьпредставляет собой кольцо, ограниченное окружностями:

0

При вычислении данного интеграла следует перейти к полярным координатам

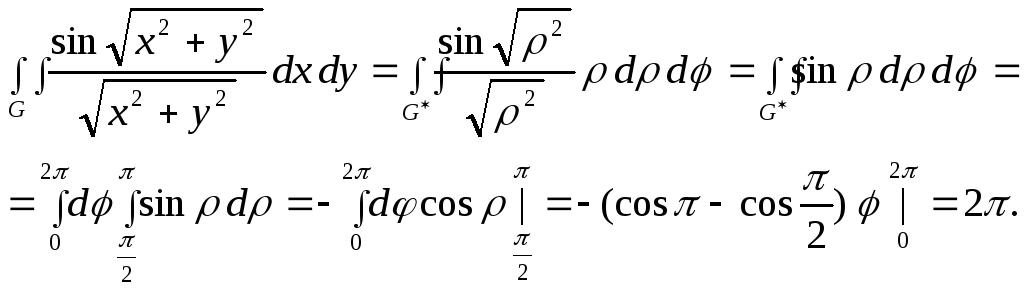
§ 4. Приложения двойных интегралов.

Как уже было сказано выше, с помощью двойного инте -грала можно вычислить площадь области или найти объём криволинейного цилиндра. Кроме этого двойной интеграл име- ет и другие приложения:

1. Вычисление массы пластинки: 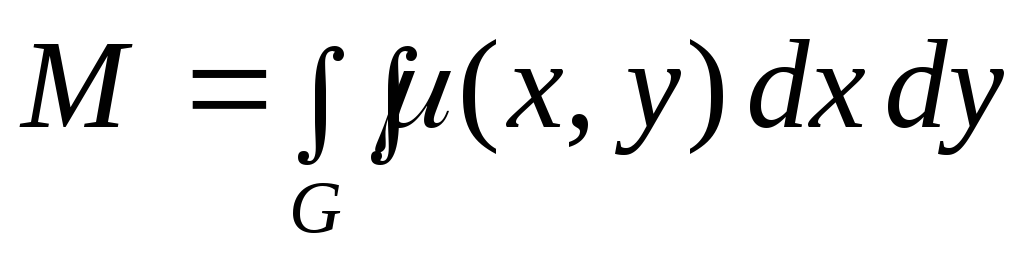, где 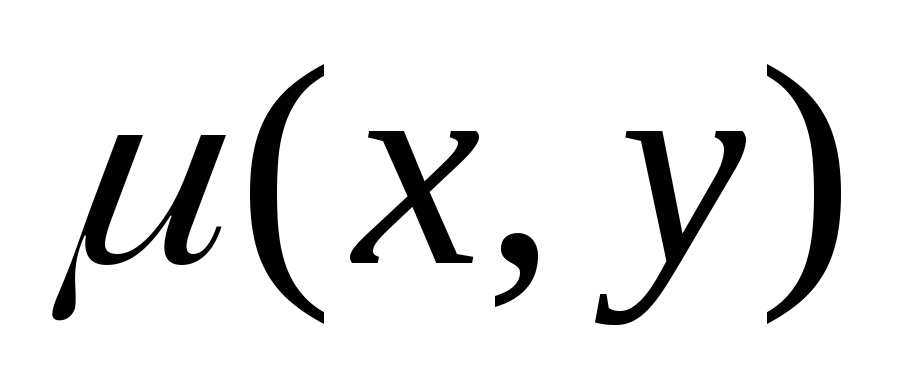- плотность масс на поверхности пластинки.

ПРИМЕР. Найти массу круга радиуса 2 с центром в начале

координат, плотность масс которого определяется по формуле: .

По формуле, применяя переход к полярным координатам, получим:

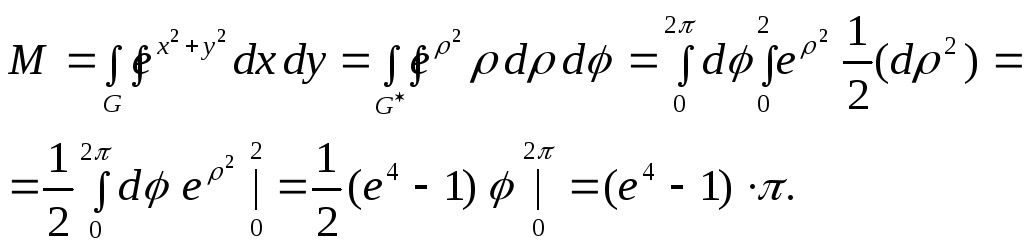
2. Вычисление координат центра масс пластинки. Если

- плотность масс пластинки, непрерывная в области функция, то координаты центра масс этой пластинки определяются формулами:

Здесь - это масса области.

В частности, если пластинка однородная, т.е. ,

то координаты центра масс определяются по формулам:

где - площадь области.

ПРИМЕР. Найти координаты центра масс однородной пластинки, ограниченной линиями:

0 1 2

Сначала найдём площадь области :

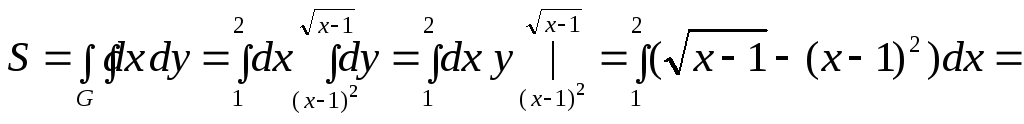
Тогда

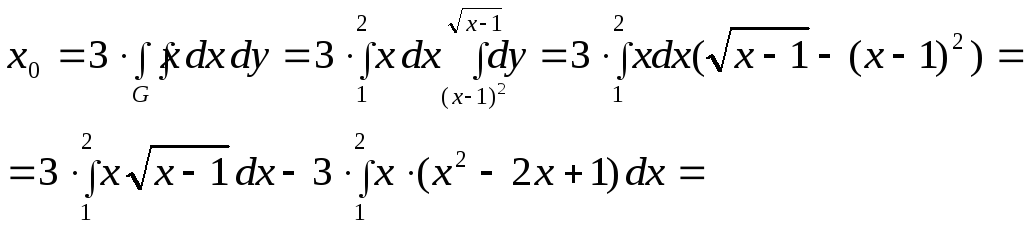
в первом интеграле сделаем замену:

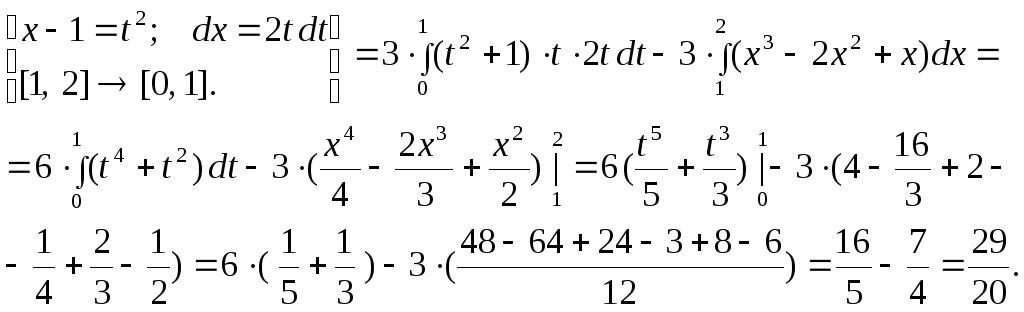
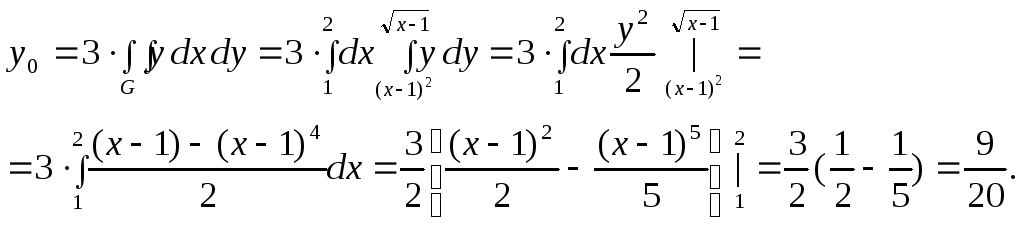
Таким образом точка

2. Вычисление моментов инерции пластинки. Известно, что момент инерции материальной точки относительно некоторой оси равен произведению массы точки на квадрат её рассто -яния от оси. Пусть область плоскости занята пластинкой, имеющей непрерывную плотность. Тогда моменты инерции этой пластинки относительно осей координат можно вычислять по формулам:

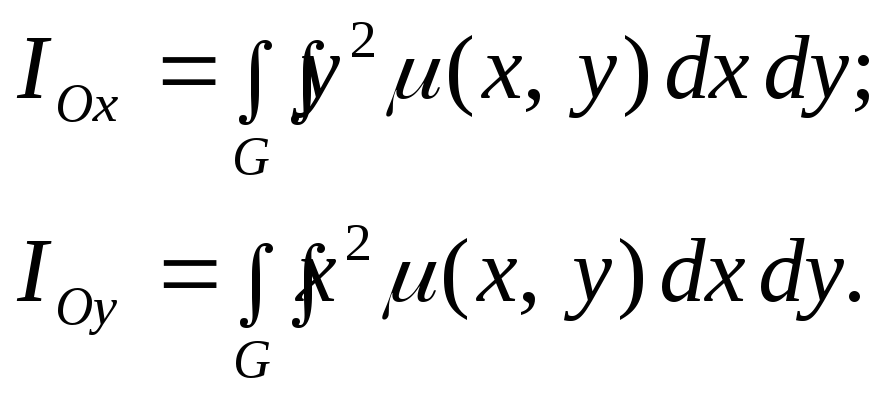
Момент инерции относительно начала координат вычисля – ется по формуле

.

ПРИМЕР. Найти момент инерции относительно оси пластинки, ограниченной линиями:если она имеет постоянную плотность

По соответствующей формуле,

-2 0 2