- •Часть 2.
- •§ 1 Первообразная и неопределённый интеграл
- •§ 2. Основные методы интегрирования
- •§ 3. Интегрирование рациональных дробей
- •§ 4. Интегрирование тригонометрических функций.
- •§ 5. Интегрирование иррациональных функций.
- •§ 1 . Основные определения и свойства.
- •§ 2. Правила вычисления определённого
- •§ 3. Некоторые геометрические приложения определённого интеграла.
- •2. Площадь криволинейного сектора.
- •§ 4. Несобственные интегралы.
- •§ 1 Основные понятия и определения
- •§ 2. Предел и непрепывность функции 2 - х
- •§ 3. Дифференцируемость функции 2 – х
- •§ 4. Производные сложных функций
- •§ 5. Производная от функции, заданной неявно.
- •§ 6. Касательная плоскость и нормаль к
- •§ 7. Производная по направлению и градиент.
- •§ 8. Частные производные высших порядков.
- •§ 9. Экстремум функции двух переменных.
- •§ 10. Наибольшее и наименьшее значение
- •§ 1. Двойные интегралы.
- •§ 2 Вычисление двойного интеграла в
- •§ 3. Замена переменных в двойном интеграле.
- •§ 4. Приложения двойных интегралов.
- •§ 5. Тройные интегралы.
- •§ 6 Криволинейный интеграл 1- го рода
§ 1. Двойные интегралы.
Пусть
![]() - замкнутая, ограниченная область в
плоскости
- замкнутая, ограниченная область в
плоскости![]() ,
а
,
а![]() - функция, определённая и ограниченная
в точках области
- функция, определённая и ограниченная
в точках области![]() .
.
Разобьём
область
![]() на
на![]() частей
частей![]() с площадями
с площадями![]() ,
не имеющих общих внутренних точек.
В каждой частичной области
,
не имеющих общих внутренних точек.
В каждой частичной области![]() возьмём произвольную точку
возьмём произвольную точку![]() и составим сумму
и составим сумму
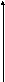





![]()
![]() ,
(1) которую назовём
интегральной
суммой
для функции
,
(1) которую назовём
интегральной
суммой
для функции
![]() в области
в области![]() .
.


![]()

![]()
![]()
О
![]()
![]()
Диаметром
области
![]() -
-![]() - называемся наибольшее расстояние
между граничными точками области
- называемся наибольшее расстояние
между граничными точками области![]() .
Пусть
.
Пусть![]() .
.
Определении
1.
Если интегральная сумма (1) при
![]() имеет конечный предел
имеет конечный предел![]() ,
то этот предел называетсядвой
-ным интегралом
от функции
,
то этот предел называетсядвой
-ным интегралом
от функции
![]() по области
по области![]() и обозначается:
и обозначается:
![]() .
(2)
.
(2)
В
этом случае функция
![]() называется
интегри-
руемой
в области
называется
интегри-
руемой
в области
![]() ,
,![]() называется
областью
интегриро-вания,
а
называется
областью
интегриро-вания,
а
![]() -элементом
площади.
-элементом
площади.
Если
функция
![]() непрерывна (или кусочно - непре- рывна)
в области
непрерывна (или кусочно - непре- рывна)
в области![]() ,
то она интегрируема в этой области.
,
то она интегрируема в этой области.
Геометрический
смысл двойного интеграла:![]() Двойной
интеграл численно равен объёму
криволинейного
цилиндра,
ограниченного сверху графиком
неотрицательной функции
Двойной
интеграл численно равен объёму
криволинейного
цилиндра,
ограниченного сверху графиком
неотрицательной функции
![]() ;
снизу - областью
;
снизу - областью![]() ,
лежащей в плоскости
,
лежащей в плоскости![]() ,
а с боковых сторон - цилиндрической
поверхностью, обра -зующая которой
параллельна оси
,
а с боковых сторон - цилиндрической
поверхностью, обра -зующая которой
параллельна оси![]() ,
а направляющая - совпадает с границей
области
,
а направляющая - совпадает с границей
области![]() .
.
![]()
![]()












 О
О
![]()
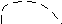

![]()
![]()
![]() (3)
(3)
В
частности, если
![]() ,
двойной интеграл равен площади
области
,
двойной интеграл равен площади
области![]() .
.
![]() (4)
(4)
СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА,
Основные свойства двойного интеграла аналогичны соот -ветствующим свойствам определённого интеграла, а именно:
1.
Постоянный множитель можно выносить
за знак инте -грала, т.е., если
![]() - интегрируема в области
- интегрируема в области![]() ,
а
,
а![]() - произвольное число, то
- произвольное число, то
![]() (5)
(5)
2. Двойной интеграл от алгебраической суммы двух (или более) интегрируемых функций равен алгебраической сумме этих функций, т.е
![]() ;
(6)
;
(6)
3.
Если область является объединением
двух областей
![]() ,
не имеющих общих внутренних точек,
то для интегрируемой в области
,
не имеющих общих внутренних точек,
то для интегрируемой в области![]() функции выполняется свойство:
функции выполняется свойство:
![]() ;
(7)
;
(7)
4.
Теорема
о среднем.
Если функция
![]() инте -грируема в области
инте -грируема в области![]() ,
то в этой области найдётся точка
,
то в этой области найдётся точка![]() ,
такая, что для всех точек области
выпол -няется следующее равенство:
,
такая, что для всех точек области
выпол -няется следующее равенство:
![]() ,
(8)
,
(8)
где
![]() - площадь области
- площадь области![]() .
.
§ 2 Вычисление двойного интеграла в
ДЕКАРТОВЫХ КООРДИНАТАХ (ПЕРЕХОД ОТ
ДВОЙНОГО ИНТЕГРАЛА К ПОВТОРНОМУ)
Определение.
Область
![]() называетсяправильной
в на -правлении оси
называетсяправильной
в на -правлении оси
![]() ,
если любая вертикальная ( гори-
зонтальная ) прямая, пересекающая
область
,
если любая вертикальная ( гори-
зонтальная ) прямая, пересекающая
область![]() ,
пересекает её границу не более чем
в двух точках.
,
пересекает её границу не более чем
в двух точках.
Пусть
область
![]() правильная в направлении оси
правильная в направлении оси![]() .
Тогда выполняется следующая терема:
.
Тогда выполняется следующая терема:
ТЕОРЕМА
1 Пусть функция
![]() определена в области
определена в области![]() ,
где
,
где
![]() непрерывные
функции на промежутке
непрерывные
функции на промежутке
![]() .
Пусть в области
.
Пусть в области![]() существует двойной интеграл
существует двойной интеграл
![]() ;
(1)
;
(1)
и
пусть для каждого
![]() существует определённый интеграл
вида
существует определённый интеграл
вида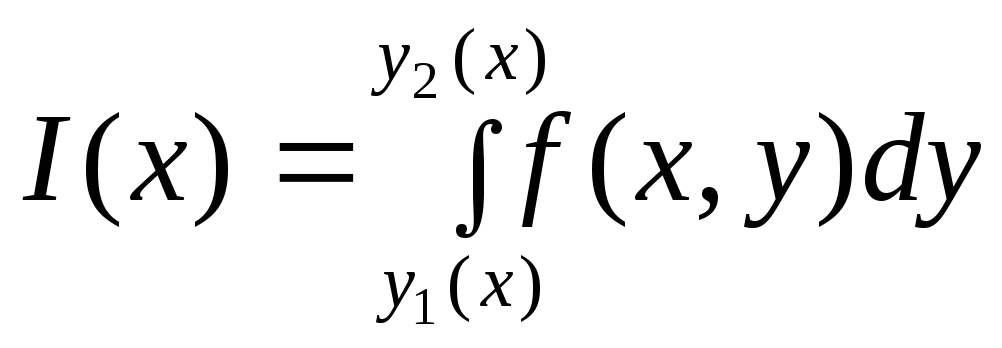 .
Тогда существует опре-
.
Тогда существует опре-
делённый
интеграл
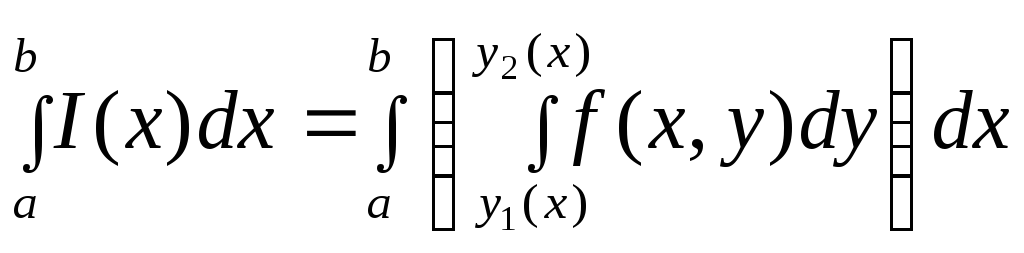 и спра -ведливо равенство:
и спра -ведливо равенство:
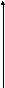
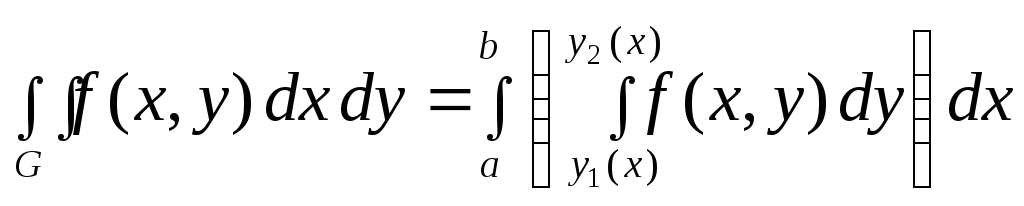 .
(2)
.
(2)



![]()



![]() -
-
![]()
-----![]()
О
![]()
![]()
![]()
Аналогичная формула имеет место и в случае, если область является правильной относительно другой оси:






![]()
![]()

--
![]() ---
---![]()
![]()

![]()
O x
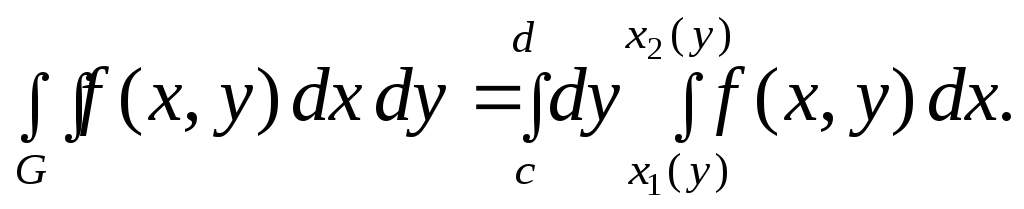 (3)
(3)
Формулы (3) и (4) определяют переход от двойного интеграла к повторному (т.е. интеграл от интеграла)
Порядок интегрирования, обычно, выбирают в соответствии с ориентацией области (область должна быть правильной в направлении интегрирования, чтобы можно было обойтись одним интегралом (если это возможно), и не пришлось бы дробить область на несколько правильных частей). Если же область интегрирования является правильной в обоих направ- лениях, то порядок интегрирования выбираем таким образом, чтобы легче вычислялся внутренний интеграл.
ПРИМЕРЫ.
Изменить порядок интегрирования:
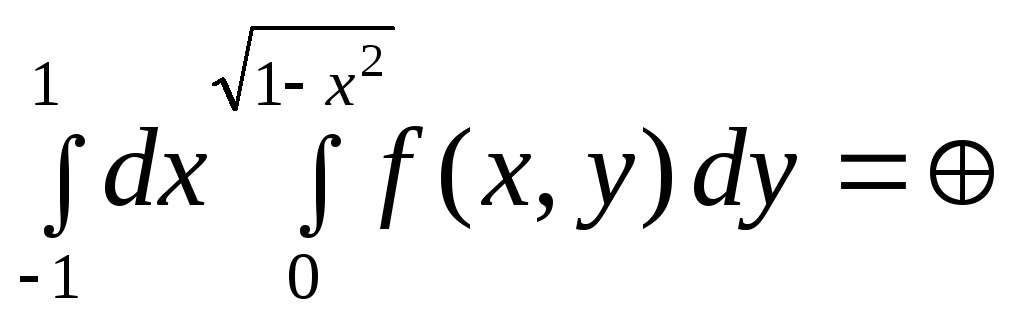
Область интегрирования определяется неравенствами:
![]() Построим
эту область.
Построим
эту область.
![]() ,
тогда это верхняя половина окружности
,
тогда это верхняя половина окружности
![]()


![]()






 1
1















 -1
0 1
-1
0 1
![]()
Если
мы теперь изменим порядок интегрирования,
то в данной области
![]() ,
а
,
а![]() меняется от левой половины окружности
меняется от левой половины окружности![]() до правой половины окружности
до правой половины окружности![]() и интеграл преобразуется к виду:
и интеграл преобразуется к виду:
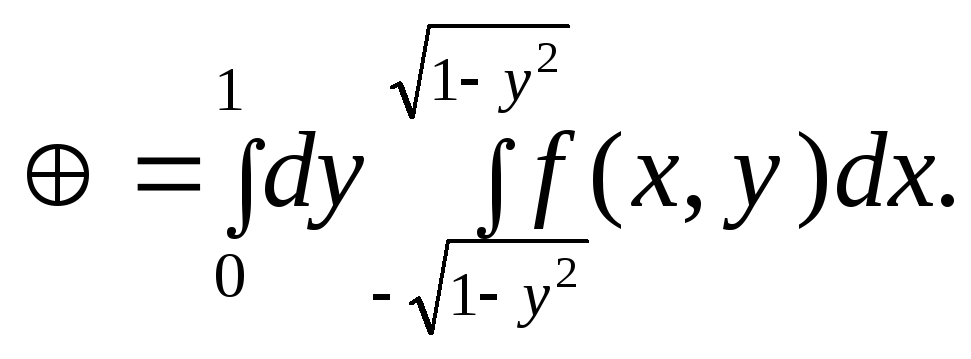
Изменить порядок интегрирования:
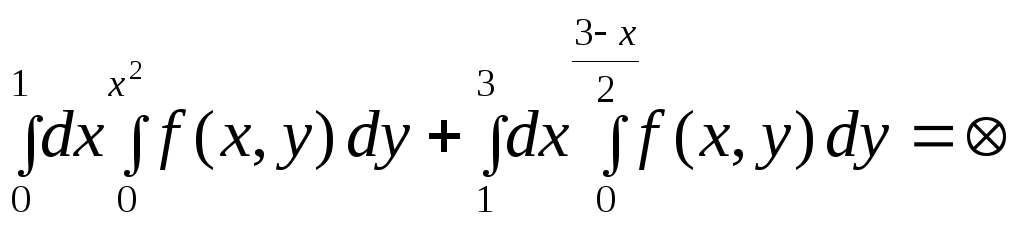
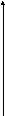







 Для
первого интеграла
Для
первого интеграла
![]() ;
для второго интеграла
;
для второго интеграла![]() .
Таким образом
.
Таким образом![]() .
Построим эту область.
.
Построим эту область.
![]()
 1,5
1,5
1

0
1 3
![]()
Переориентируем
её в направлении оси
![]() .
Теперь в этой области:
.
Теперь в этой области:![]() и исходная сумма двух интегралов
перейдёт в один интеграл:
и исходная сумма двух интегралов
перейдёт в один интеграл:
![]()
Заметим, что при таком порядке интегрирования интеграл будет вычисляться проще.
Вычислить двойной интеграл:
![]() ,
где
,
где
![]()
Построим
область
![]()
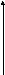
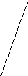

![]() -
-![]() _
_![]()





 3
3
![]()
1
0
1
![]()
Область является неправильной по обоим осям. Поэтому при вычислении интеграла область придётся разбивать на две части и, соответственно, интеграл будет равен сумме двух интегралов:
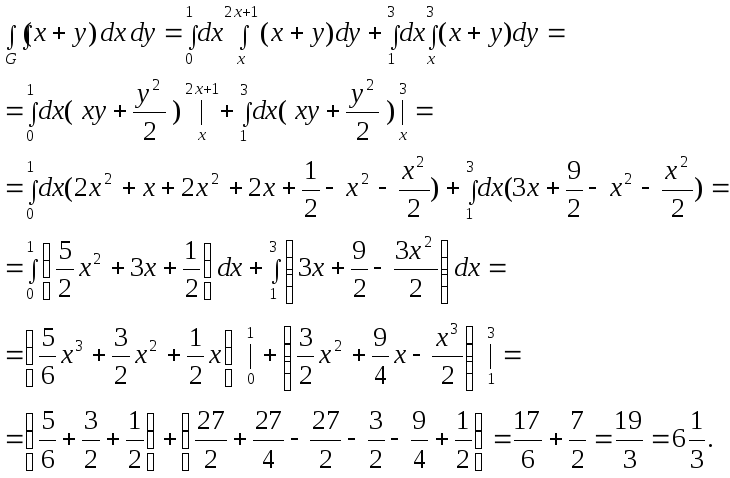
Вычислить двойной интеграл:
![]()
![]() ,где
,где
![]()
Построим
область
![]()





![]()
![]()


![]()
0
![]()
Данная
область является правильной в
направлении обеих осей координат,
поэтому порядок интегрирования можем
выбирать произвольным образом. В
этом случае следует обратить внимание
на подынтегральную функцию
![]() .
.
Если
внутренний интеграл поставить по
переменной
![]() ,
то при вычислении интеграла придётся
дважды применять формулу интегрирования
по частям, что, естественно, не
целесообразно (получаются громоздкие
вычисления). Поэто- му следует выбрать
другой порядок интегрирования:
,
то при вычислении интеграла придётся
дважды применять формулу интегрирования
по частям, что, естественно, не
целесообразно (получаются громоздкие
вычисления). Поэто- му следует выбрать
другой порядок интегрирования:
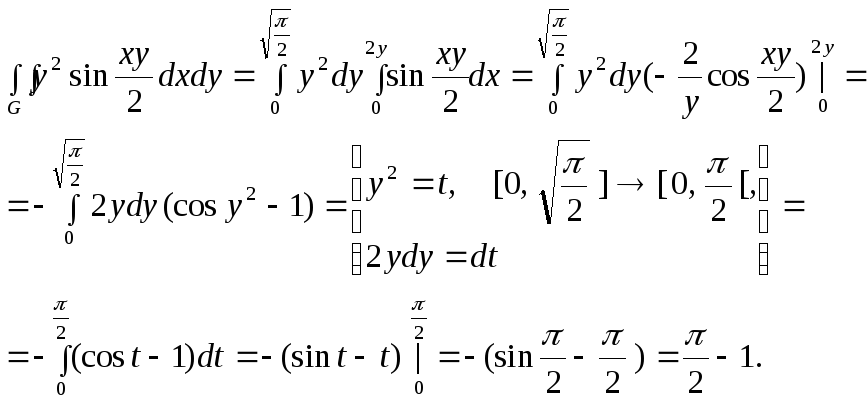
Найти площадь фигуры, ограниченной линиями:
![]()
![]()
Построим
область
![]() .
.

![]()
 2
2
 -1
0 8
-1
0 8
![]()

![]()

 -6
-6
Найдём точки пересечения графиков:
![]()
Корни
этого уравнения
![]()
Область
ориентирована вдоль оси
![]() ,
поэтому следует выбрать следующий
порядок интегрирования:
,
поэтому следует выбрать следующий
порядок интегрирования: