§ 6 Криволинейный интеграл 1- го рода

Можно обобщить понятие определённого интеграла на случай, когда областью интегрирования является не отрезок числовой прямой, а некоторый участок кривой, лежащей в плоскости.

Рассмотрим на плоскости некоторую кривую, за -данная параметрическими уравнениями:Эта кривая называетсягладкой на промежутке , если для всех точек этого промежутка функциинепрерывны и не обращаются в нуль одновременно. Непре -рывная кривая, состоящая из конечного числа гладких кусков, называетсякусочно – непрерывной .

Пусть функция определена и ограничена на множестве точек, лежащих на гладкой или кусочно –гладкой кривой. Разобьём эту кривую произвольным образом начастей точками. На каждой из частичных дуг возьмём фиксированную точку

и составим сумму , где- длина дуги. Эта сумма называетсяинтегральной суммой для функции по кривой. Пусть- максимальная из длин частичных дуг.

Определение. Если существует конечный предел , то этот предел называетсякриволинейным интегралом перво- го рода от функции по кривойи обозначается

. (1)

В этом случае функция называетсяинтегрируемой вдоль кривой , а сама эта кривая называетсяконтуром интегрирования.

Геометрический смысл криволинейного интеграла 1 – го рода. Если определённый интеграл - это площадь криволи -нейной трапеции, то криволинейный интеграл численно равен площади поверхности криволинейной цилиндрической поверх- ности, образующая которой параллельна оси , направляя- ющая совпадает с кривой, а верхний контур состоит из значений функциипо контуру

А

0 В у

х

ОСНОВНЫЕ СВОЙСТВА КРИВОЛИНЕЙНОГО

ИНТЕГРАЛА 1 –ГО РОДА

1. Криволинейный интеграл 1 – го рода не зависит от пути интегрирования:

2.

3.

4. Если - некоторая точка на дуге, то

ВЫЧИСЛЕНИЕ КРИВОЛИНЕЙНОГО

ИНТЕГРАЛА 1 – ГО РОДА.

Криволинейный интеграл первого рода легко сводится к определённому интегралу.

1. Если кривая задана параметрическими уравнениями:

, где и- непрерывно дифференцируемые функции при, то

(2)

причём значение соответствует точке, а- точке

ПРИМЕР. Вычислить интеграл: , где

где

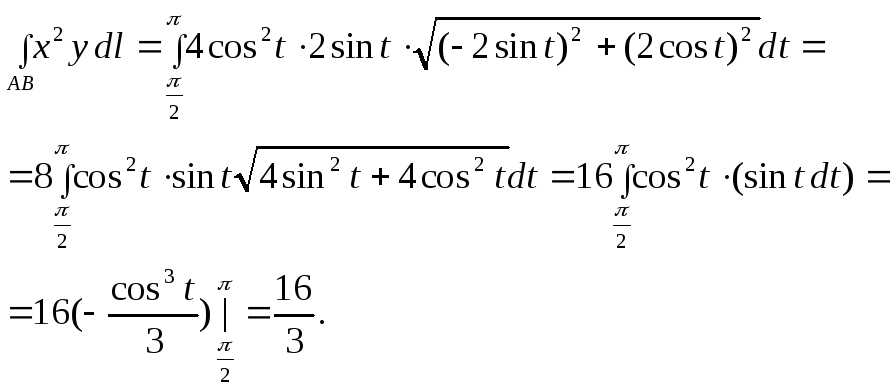
Если - пространственная кривая, заданная уравне -ниями:

формула (2) приобретает вид:

В частности, если кривая задана уравнениемгде- непрерывно диффе -ренцируемая функция, то формула (2) приобретает вид:

(3)

ПРИМЕР. Вычислить криволинейный интеграл:

Решение. тогда

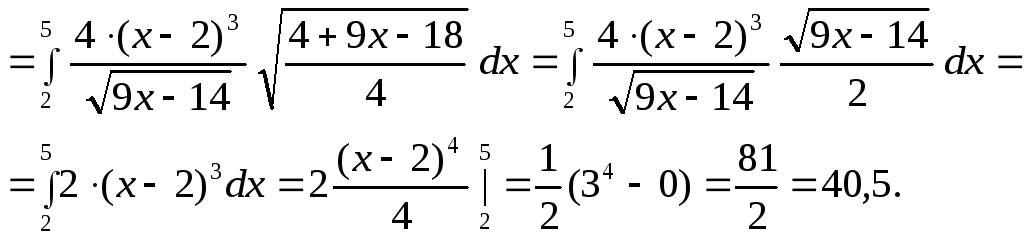
Если кривая задана уравнением в полярных коорди -натах, т.е.то получаем ещё один частный случай формулы (2):

ПРИМЕР. Вычислить криволинейный интеграл:

Решение.

=

Тогда

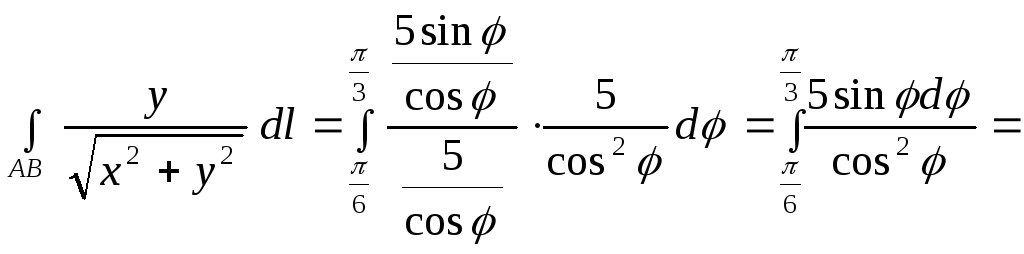
Сделаем замену переменной

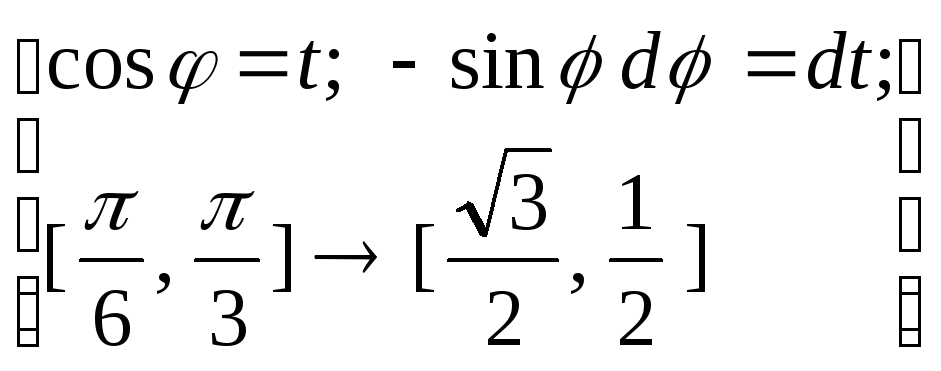
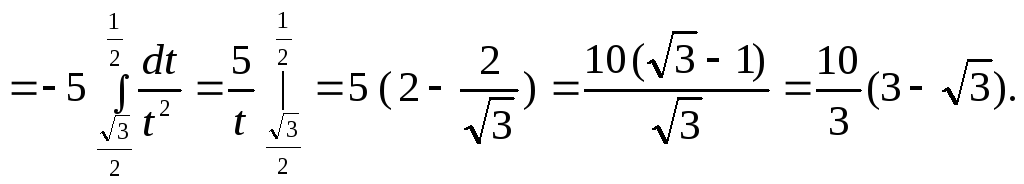
ЗАКЛЮЧЕНИЕ

Данное учебное пособие поможет студентам заочной формы обучения выполнить соответствующие контрольные работы и подготовиться к экзаменам по соответствующим разделам математики.

108