§ 4. Производные сложных функций

Пусть - функция двух переменных, каждая из которых, в свою очередь является функцией независимой пе- ременной, т.е.. Тогда функцияявляется сложной функцией переменнойПеременныеипри этом называются промежуточными. Тогда выполняется следующая теорема:

ТЕОРЕМА. Если функции дифферен -цируемы в точке, функциядифференцируема в точке, то сложная функциятакже дифференцируема в точкеи производная этой функции (как функции одной переменной) вычисляется по формуле:

. (1)

Замечание. Следует обратить внимание на то, что если в обозначении производной стоит , то функция зависит от двух и более переменных, если же , то функция зависит только от одной переменной.

ПРИМЕРЫ. 1. Пусть

Тогда, по формуле (1),

(В полученную производную вместо иможем подставить их выражения).

2. Пусть

Тогда . Таким образом,

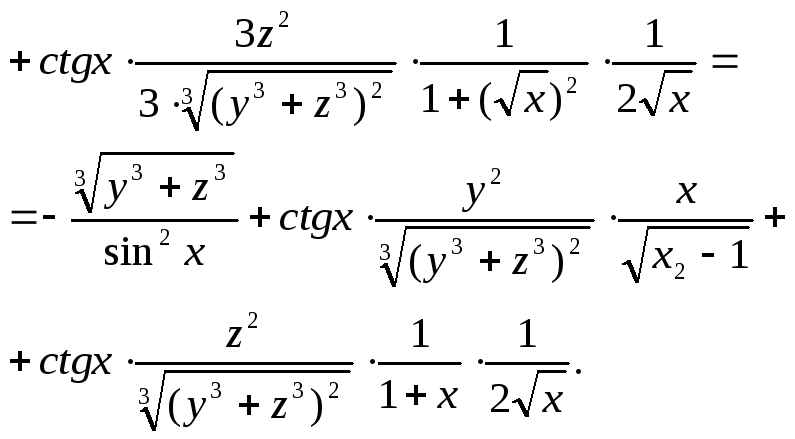
3. Пусть теперь - функция двух переменных, а- также функции двух перемен - ных. Тогдасложная функция двух переменныхи мо -жем найти её частные производные по этим переменным сле- дующим образом:

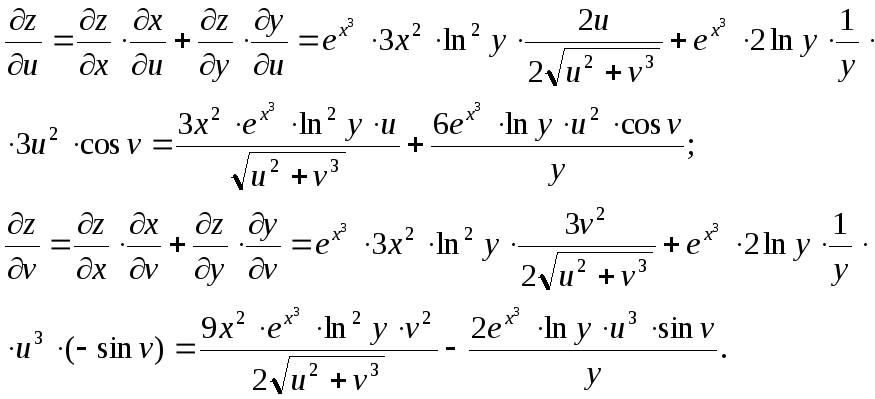
§ 5. Производная от функции, заданной неявно.

Пусть некоторая функция отопределяется уравне - ниемТогда имеет место следующая теорема:

ТЕОРЕМА. Если непрерывная функция отзадана уравнением, где- непрерывные функции в некоторой области, причём в этой

области , то функцияотимеет производную и выполняется формула

(1)

ПРИМЕР: Тогда, так как левая часть равна, то,

и

Рассмотрим теперь неявно заданную функцию двух пере -менных . Если считатьпостоянной, то по фор- муле (1),, если считатьпостоянной, то. Аналогичным образом определяются частные производные от неявно заданных функций любого числа пере- менных.

ПРИМЕРЫ.

1, .

Левая часть равенства - это . Поэтому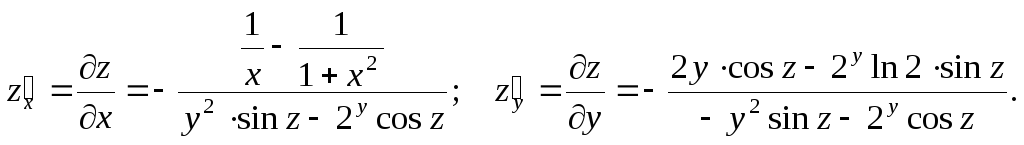

2. Тогда

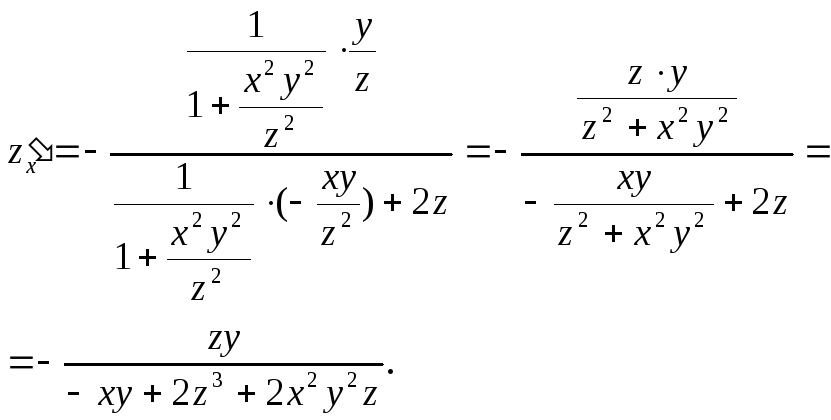
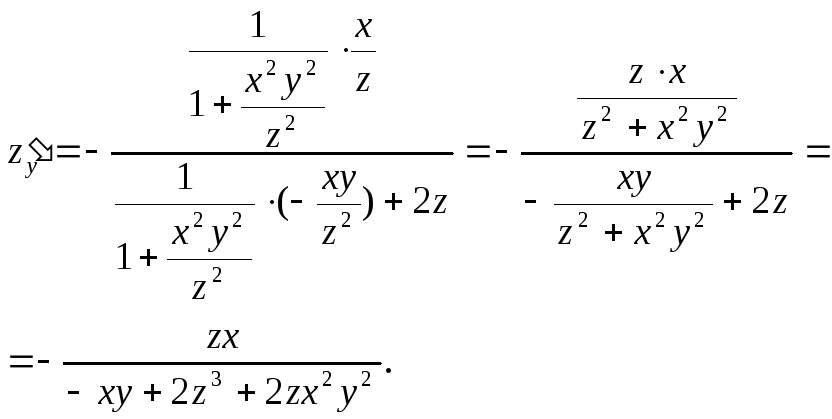
§ 6. Касательная плоскость и нормаль к

ПОВЕРХНОСТИ.

Пусть поверхность задана уравнением.

Определение 1. Касательной плоскостью к поверхности в точкеназывается плоскость, которая содер –жит касательные, проведённые в точкек каждой кривой, лежащей на поверхностии проходящей через точку.

Нормальный вектор этой плоскости

перпендикулярен к касательной каждой кривой, лежащей на поверхности и проходящей через точку. Уравнение касательной плоскости имеет вид:

Определение 2. Нормалью называется прямая, перпендику -лярная к касательной плоскости, проходящая через точку ка –сания. Её уравнение имеет вид:

ПРИМЕРЫ:

1. Написать уравнения касательной плоскости и нормали к поверхности, проходящей через точку , если по - верхностьзадана уравнением :

Левая часть этого равенства - это . Тогда:

Тогда уравнение касательной плоскости имеет вид:

или

Уравнение нормали:

2. Написать уравнение касательной плоскости и нормали

к поверхности :в точке

Уравнение поверхности перепишем в виде

.

Тогда

Уравнение касательной плоскости имеет вид:

, или

Уравнение нормали: