§ 2. Предел и непрепывность функции 2 - х

ПЕРЕМЕННЫХ.

Определение 1.-окрестностью точки называется множество точек плоскости, удовлетворяющих условию:

Определение 2. Последовательность точек называется сходящейся к точке ,если для любого существует номер, начиная с которого (т.е. для всех) все точкисодержатся в- окрест -ности этой точки.

Определение 3. Число называетсяпределом функции при, если для любой после- довательности точек, сходящейся к точке , последовательность значений функции в этих точ- ках . Или, другими словами, числоназы- ваетсяпределом функции при, если для любогосуществует, такое что для всех точек, попадающих в- окрестность точки , выполняется неравенство : , или.

Это обозначается таким образом:

Определение 4. Функция называется непре -рывной в точке , если

Определение 5. Функция непрерывная в каждой точке некоторой области, называется непрерывной в этой области.

Например, функция непрерывна в каждой точке плоскости; функциянепрерывна везде, кроме точки.

§ 3. Дифференцируемость функции 2 – х

ПЕРЕМЕННЫХ. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ.

1. Частные производные функции 2-х переменных

Пусть функция определена в некоторой областиплоскости. Пусть, далее точки

.

Полным приращением данной функции в точке называется разность:

. (1)

Если при вычислении приращения меняем только одну переменную, другую оставляя без изменения, то получим соответствующие частные приращения:

, (приращение по ), (2)

, (приращение по ), (3)

Если равенство (2) разделить на и перейти к пределу при, то получимчастную производную функции по переменной, которая обозначается следую-щим образом:

. (4)

Аналогичным образом вводится частная производная функции по переменной:

(5)

ПРИМЕРЫ: Найти частные производные следующих функций.

1. . Тогда

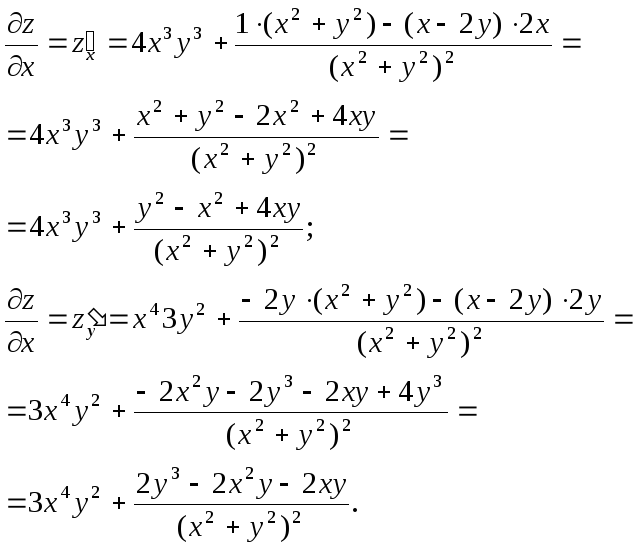
2.

Найдём частные производные

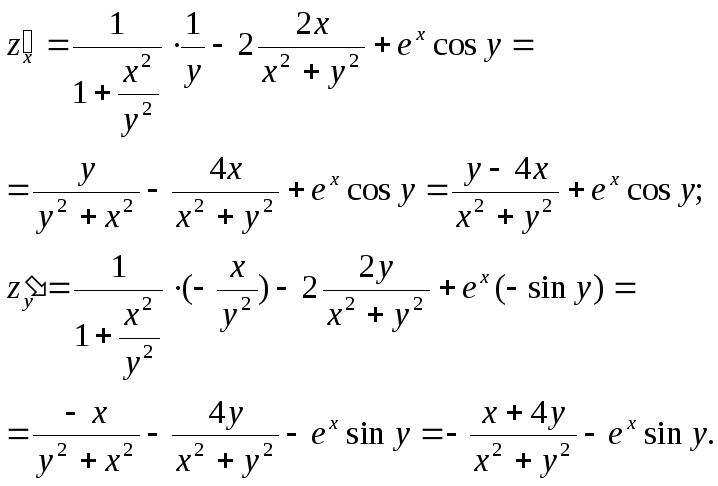
3.

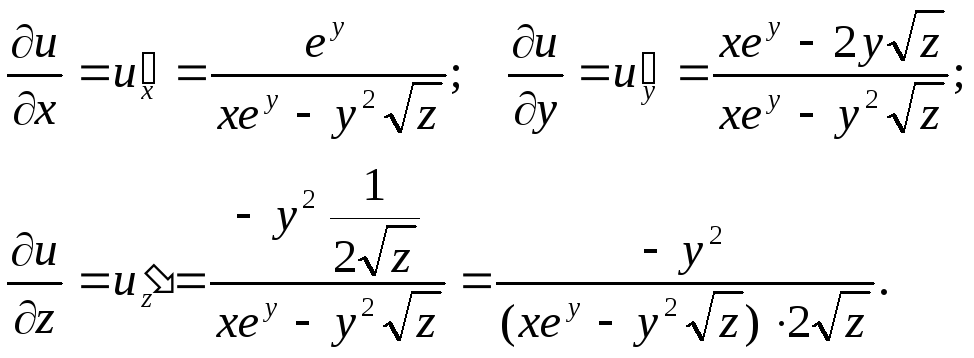
При вычислении частных производных следует помнить следующие правила:

2. Дифференцируемость функции 2-х переменных.

Пусть функция определена в некоторой области

плоскости .

Определение 1. Функция называется диффе -ренцируемой в некоторой точке области, если её полное приращениев этой точке можно представить в виде:

(1)

где - бесконечно малые функции, а- некоторые постоянные.

Определение 2. Если функция дифференци -руема в точке, то главная, линейная относительночасть её приращения называетсяполным дифферен –циалом и обозначается . (2)

Необходимые условия дифференцируемости.

1. Если функция дифференцируема в точке

, то она непрерывна в этой точке.

2. Если функция дифференцируема в точке, то она имеет в этой точке частные производные, причём.

Обратные утверждение не всегда верны, т.е. из непрерывности функции двух переменных в точке , а также из существования её частных производных в этой точке, ещё не следует её дифференцируемость.

Достаточное условие дифференцируемости.

Если функция имеет частные производные в некоторой окрестности точкии эти производные непрерывны в точке, то функция дифференцируема в этой точке. В частности, из непрерывности частных произ - водных следует непрерывность самой функции.

С учётом вышеизложенного, получаем новое выражение для полного дифференциала функции:

(3)

Кроме того, в силу формулы (3),

Следовательно, получаем:

(4)

ПРИМЕР. Найти полный дифференциал функции

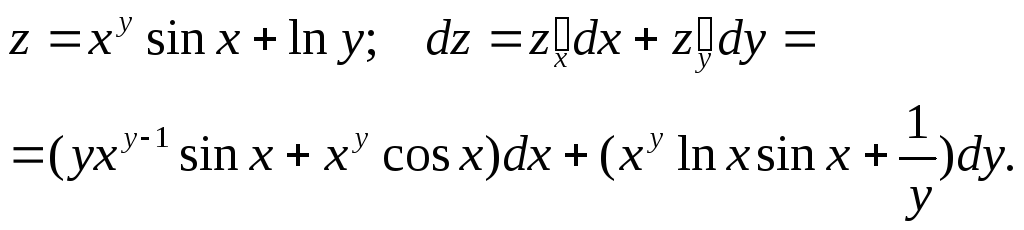
Аналогичным образом определяется дифференциал функ- ции 3-ч переменных

Например, для дифференциал равен: