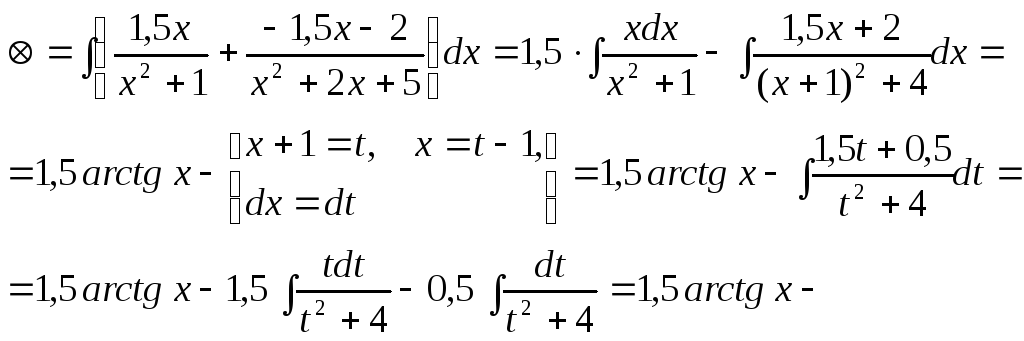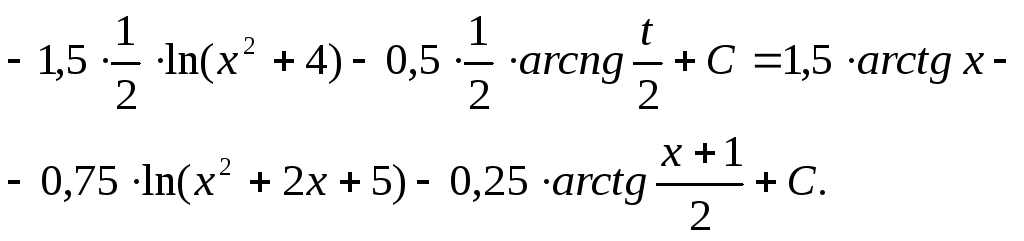§ 3. Интегрирование рациональных дробей

Определение 1. Дробно – рациональной функцией (или просто рациональной дробью) называется выражение вида

, где - многочлены степени, соответ –ственно. Если, дробь называетсяправильной. Если же , то дробь называетсянеправильной. Любую непра -вильную дробь, после деления «уголком» можно представить в виде

, где - многочлены, причём.

Например, - неправильная рациональная дробь. Разделим числитель на знаменатель «уголком»:

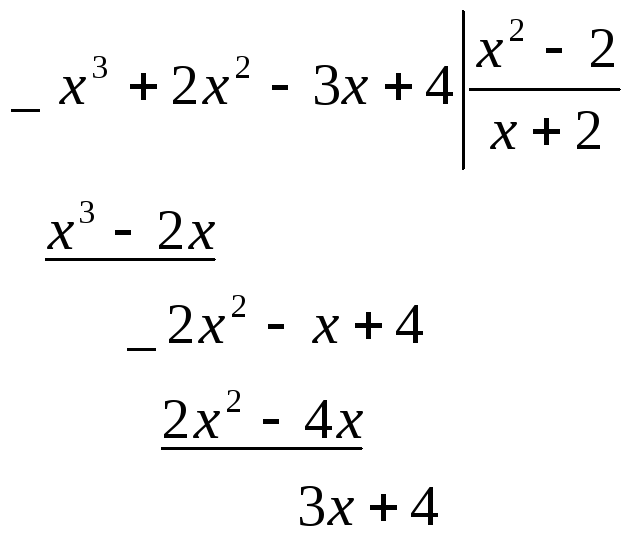
Тогда

=.

Любую правильную рациональную дробь можно с помощью метода неопределённых коэффициентов, представить в виде суммы простейших рациональных дробей. Они бывают четы-: рёх типов:

1. 2.3.

4. ( Здесь- некоторые дейст -вительные числа, а квадратный трёхчленне имеет действительных корней ).

Для дробей 1 – го и 2 - го типа выполняются формулы: Вычисление интегралов 3 – его типа рассмотрим на приме –рах:

1.

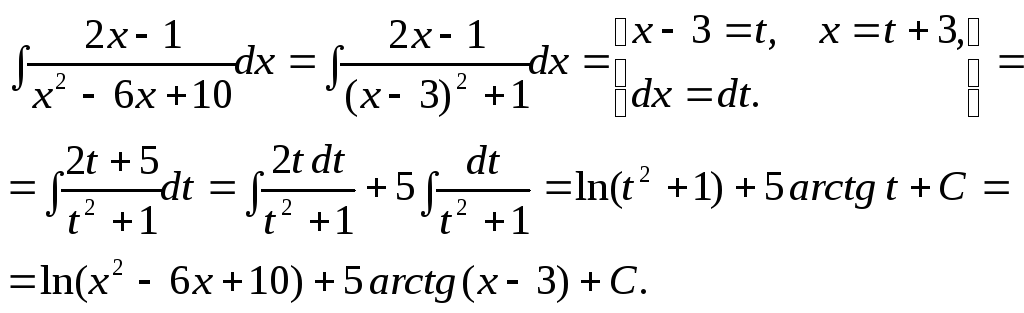
2.

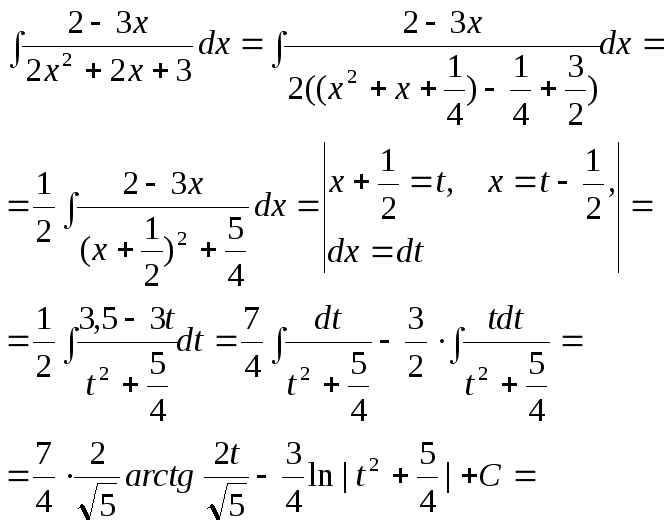
Такой же метод можно применить и в случае, если квад -ратный трёхчлен в знаменателе имеет неотрицательный дискриминант. В самом деле

3.

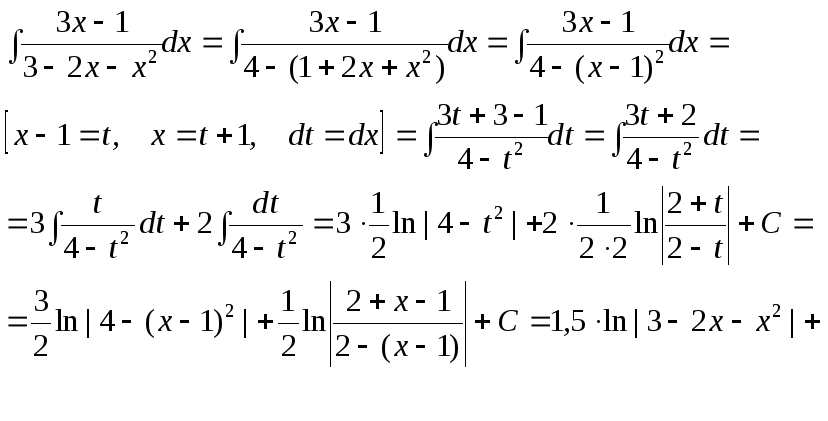
Рассмотрим теперь несколько примеров, в которых, инте- грал вычисляется разложением подынтегральной функции на простейшие дроби методом неопределённых коэффициентов.

Сначала рассмотрим самый простой случай, когда зна -менатель рациональной дроби представляет собой произве -дение нескольких различных линейных скобок :

4.

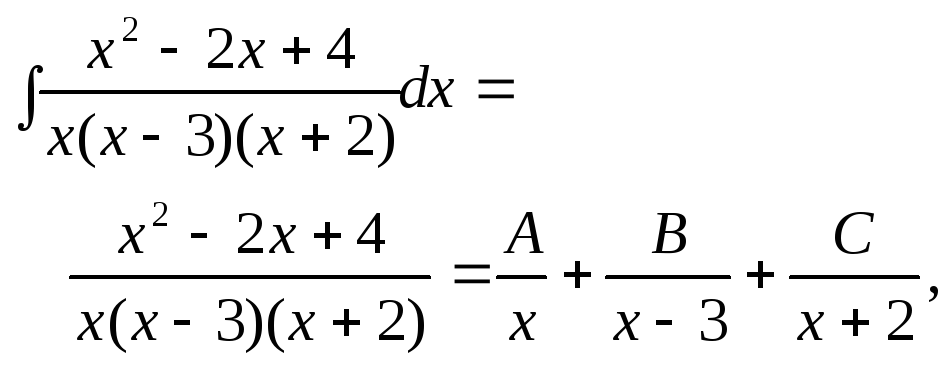
после умножения последнего равенства на общий знаменатель, получим:

Данное равенство должно выполняться для всех значений . Поэтому, приполучимили; приполучается,или; приимеем, отсюда. Тогда, возвращаясь к интегралу, получим,

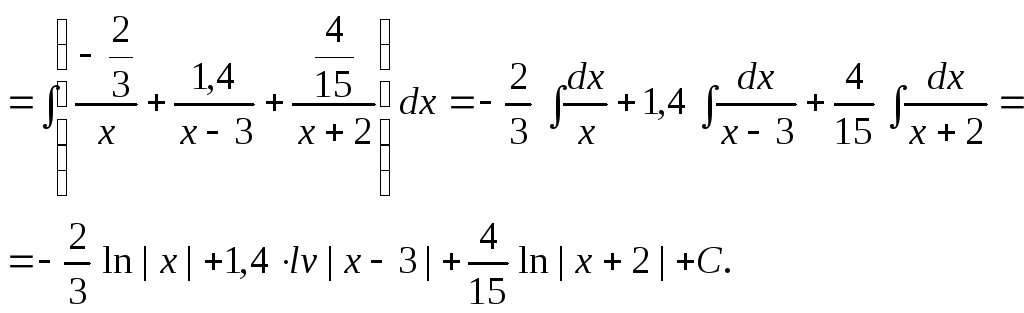
Сложнее получается, если знаменатель рациональной дро -би имеет кратные корни, т.е. содержит множитель вида . В этом случае при разложении дроби на прос -тейшие следует запомнить, что каждой скобке видаОтвечает не одно, а, слагаемых, т.е. в разложении при -сутствуют все степени данной скобки. Рассмотрим пример:

5.

Подынтегральную функцию представим в виде суммы простейших дробей:

Умножим данное равенство на общий знаменатель. Получим:

.

Раскроем все скобки:

Приравняем коэффициенты при одинаковых степенях :

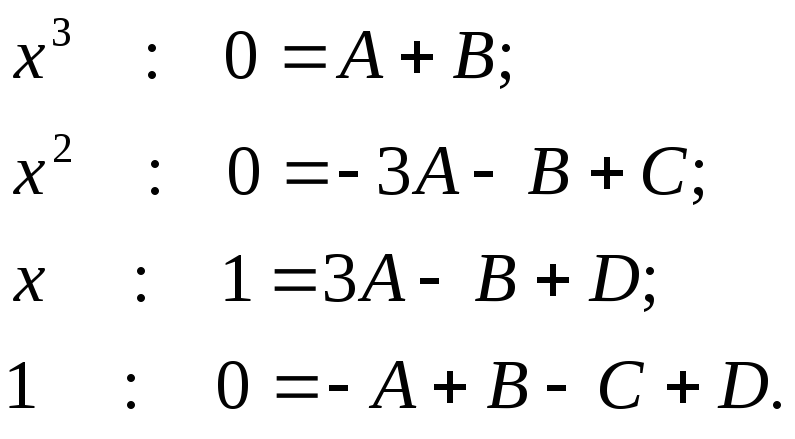
Получили систему четырёх уравнений с четырьмя неиз- вестными. Можем решить эту систему методом исключения: 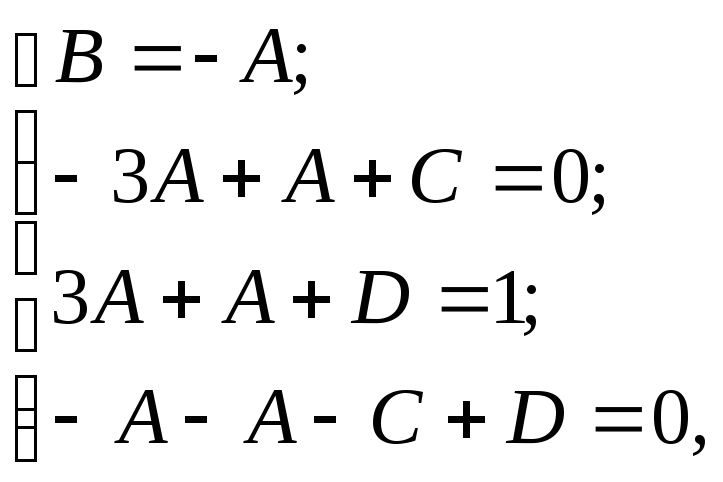или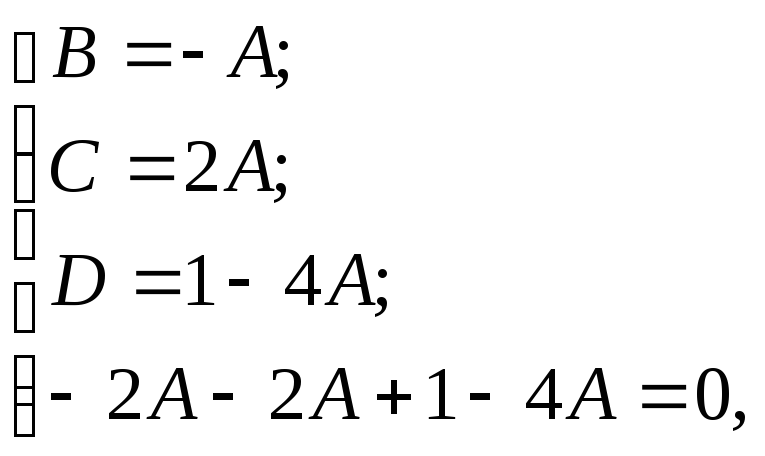

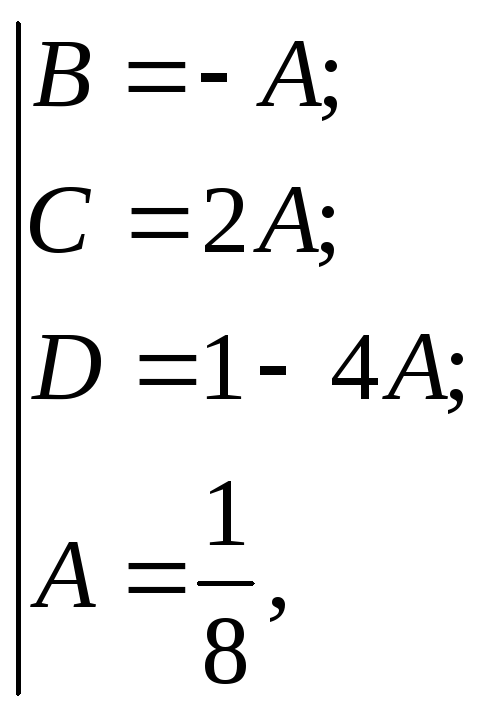следовательно

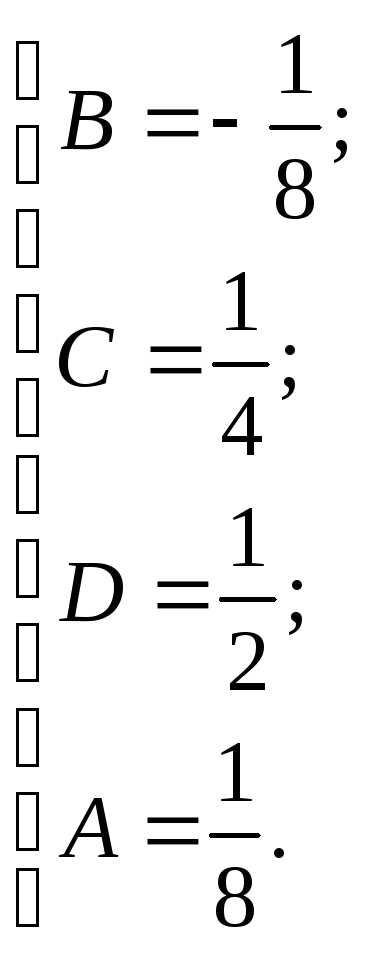
Возвращаемся к интегралу:

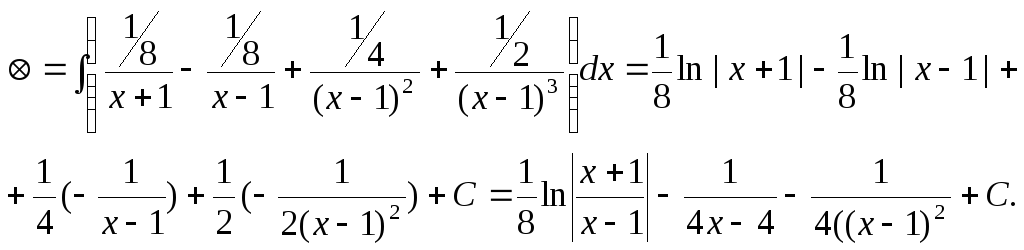Метод нахождения коэффициентов, который мы использова-ли в данном примере, называется «методом неопределённых коэффициентов».

Рассмотрим теперь более общий пример.

6.

.

Разложим подынтегральную функцию на элементарные дроби:

(скобки в знаменателе не имеют действительных корней, поэ- тому в разложении появились дроби 3–го типа). Умножив дан- ное равенство на общий знаменатель, получим:

Раскроем скобки: Приравняем коэффициенты при одинаковых степенях:

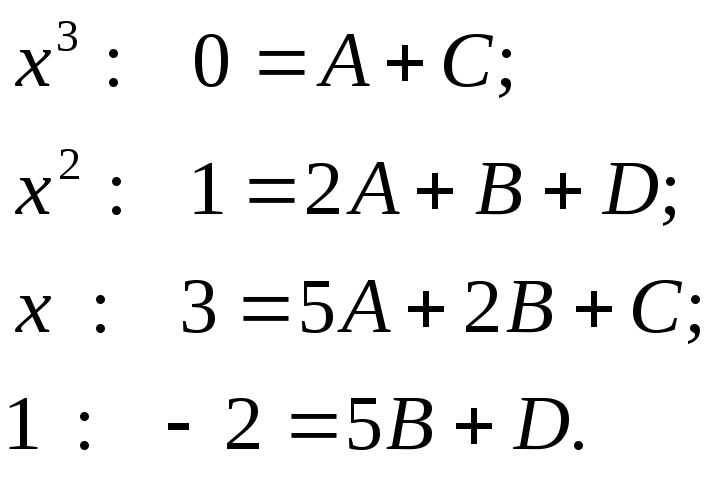
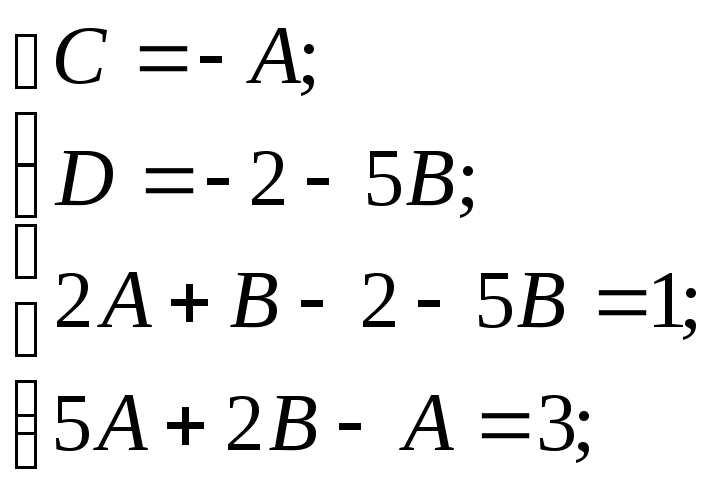
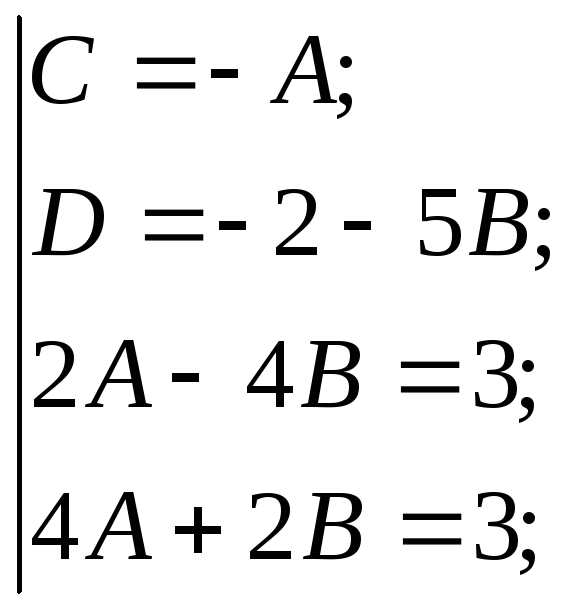
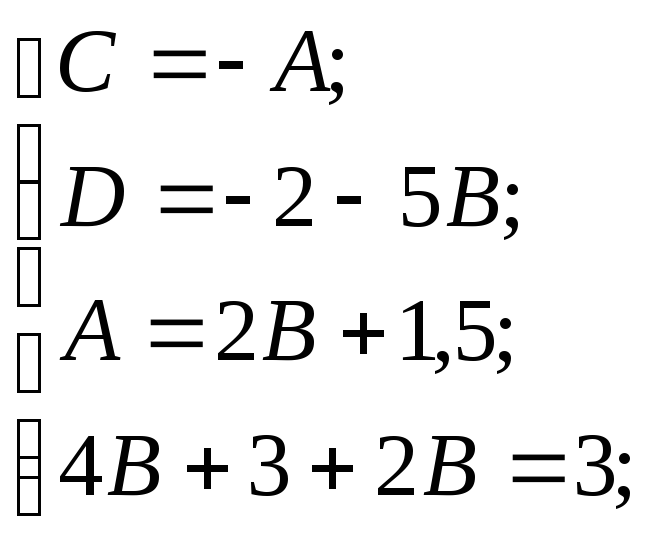
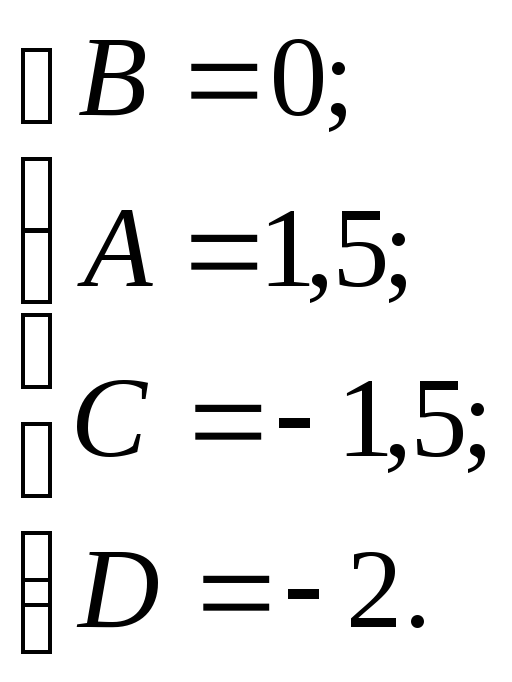
Тогда получим следующий интеграл: