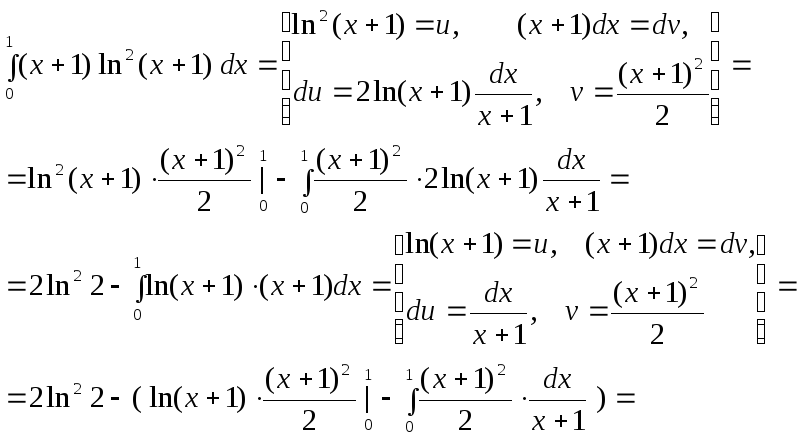§ 1 . Основные определения и свойства.

Пусть функция определена и на отрезке. Разделим этот отрезок начастей точками:. На каждом элементарном отрез- ке выберем произвольную точку. Длину элемен -тарного отрезка обозначим. Пусть. Составим сумму

. (1)

Эта сумма называется интегральной суммой для функции на отрезке. Если существует конечный предел этой суммы при, то этот предел называетсяопреде- лённым интегралом от функции на отрезкеи обозначается

. (2)

Если функция непрерывная на отрезке, то предел интегральной суммы существует и не зависит от спо -соба разбиения отрезкаи выбора точек. Числаназываются соответственнонижним и верхним пределами ин –тегрирования.

Если ина, то определённый инте -грал представляет собой площадь криволинейной трапеции, ограниченной сверху графиком функции, с боковых сторон прямыми, а снизу - осью. (Геометрический смысл определённого интеграла).

СВОЙСТВА ОПРЕДЕЛЁННОГО ИНТЕГРАЛА:

1. 2.

3. для любых точек выполняется равенство

;

4.

5. ; (- постоянный множитель):

6. Если для всех выполняется неравенство:

, то

7. Если для всех 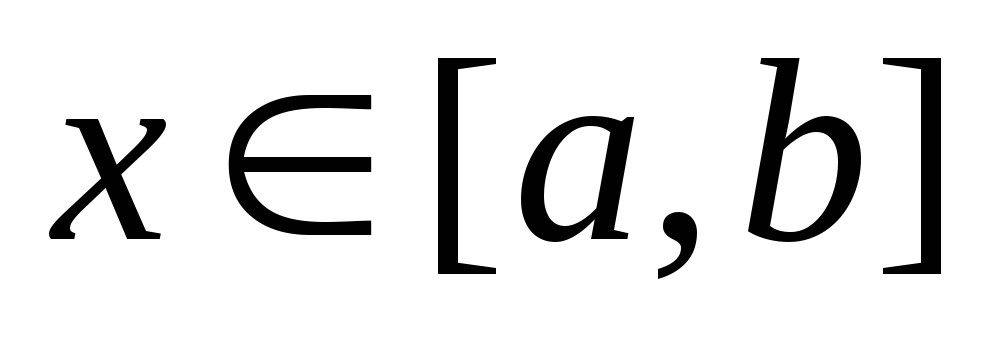выполняется неравенство:

, то для интеграла выполняется анало –

гичное неравенство: :

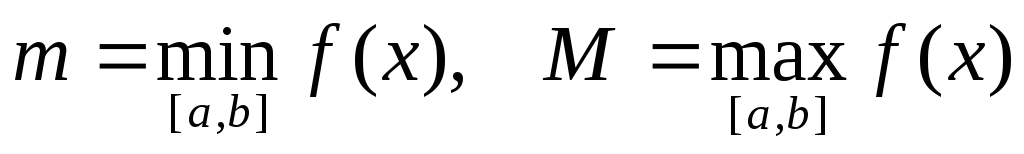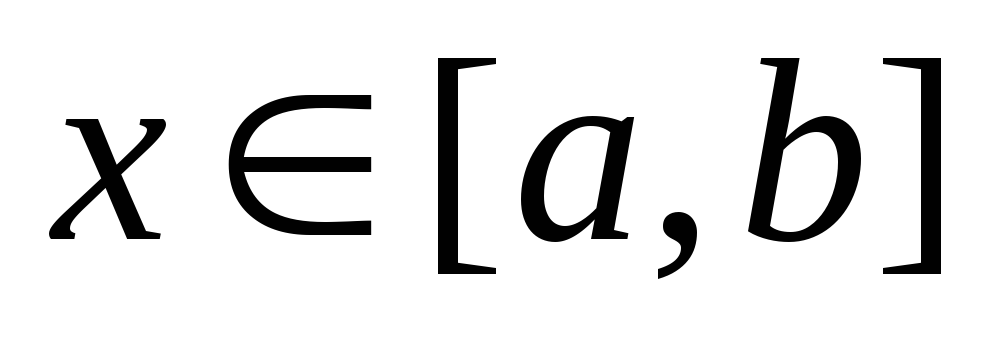7. Если , т.е. для всехвыполняется неравенство,

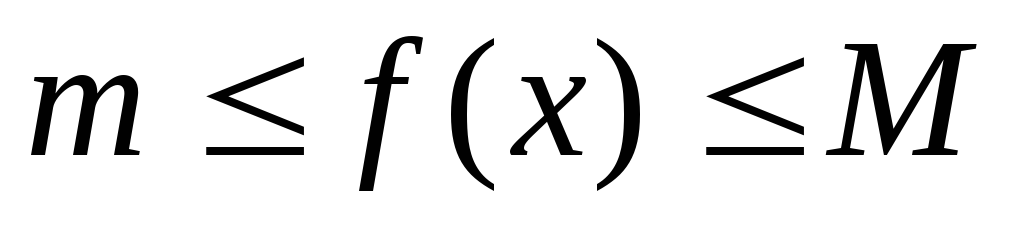то ;

7. (Формула среднего значения) Если функция 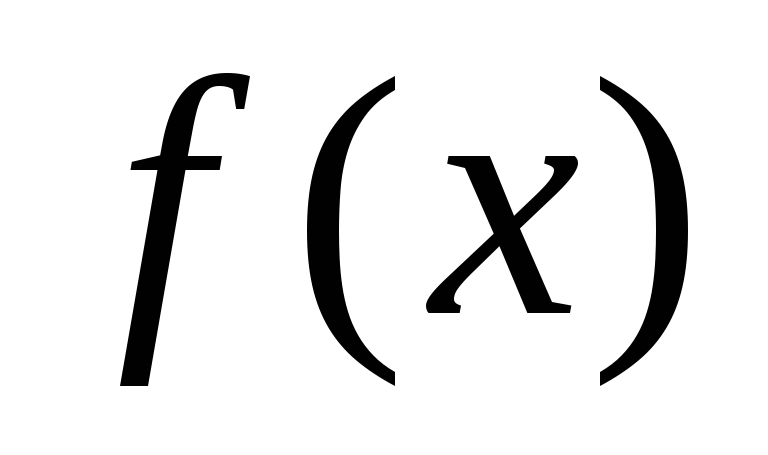не- прерывна на отрезке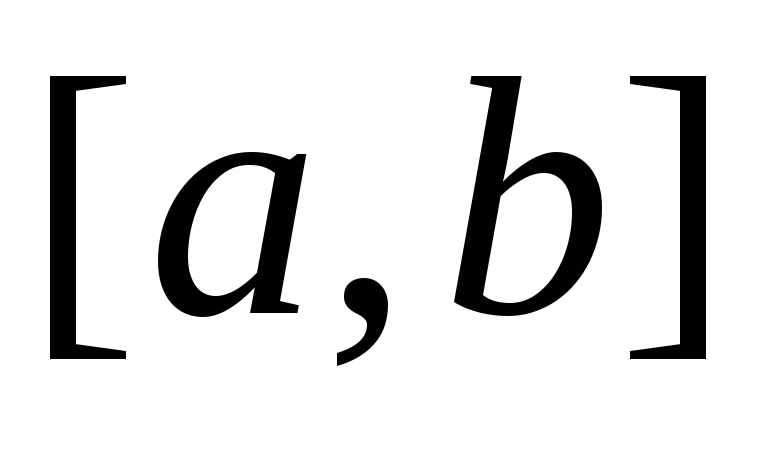, то на этом отрезке существует точкатакая, что

Замечание. Формула среднего значения имеет простой геометрический смысл: величина определённого интеграла при численно равна площади прямоугольника, имеющего высотуи основание - отрезок длины.

§ 2. Правила вычисления определённого

ИНТЕГРАЛА.

1. Формула Ньютона – Лейбница.

Если функция непрерывна на отрезкеикакая – либо её первообразная на, то имеет место формула, которая называетсяформулой Ньютона – Лейбница:

ПРИМЕРЫ:

1.

2.

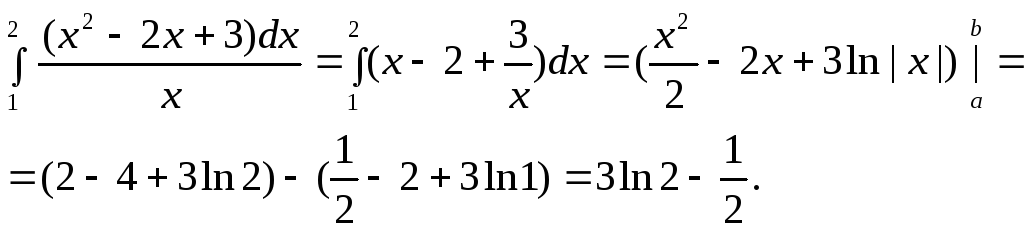
2. Замена переменной в определённом интеграле.

Пусть - непрерывная функция на отрезке, а функциянепрерывна и дифференцируема на от –резкетаком, что. Тогда справедлива формула:

.

Если применяем эту формулу «слева – направо» - то это формула подстановки (т.е. вместо подставляем некоторую функцию, а если в другую сторону (т.е. некоторую функцию заменяем новой переменной, то это формула замены пере- менной в определённом интеграле.

При выполнении замены переменной или подстановки ис -пользуются те же методы, что и при вычислении неопреде -лённого интеграла. Следует только иметь ввиду следующее замечание.

ЗАМЕЧАНИЕ. После замены переменной в определённом интеграле нет необходимости возвращаться к исходной пере- меной. Требуется только изменить пределы интегрирования в соответствии с заменой, т.е определить границы изменения новой переменной.

ПРИМЕРЫ

1.

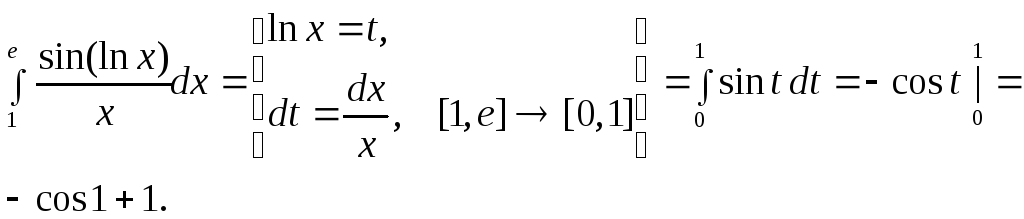
2.

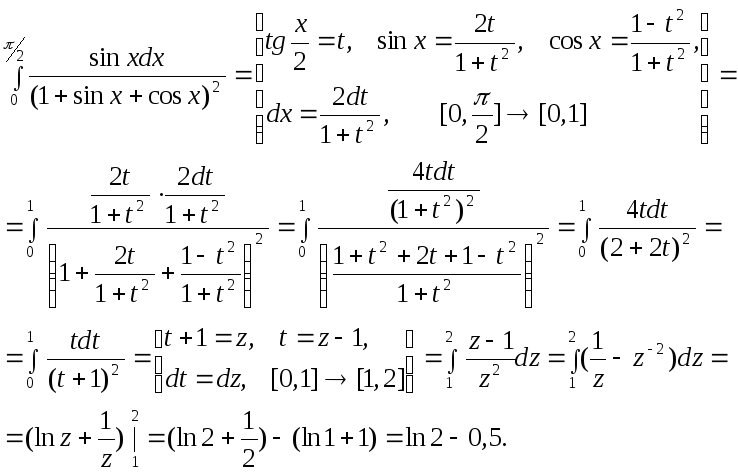3.

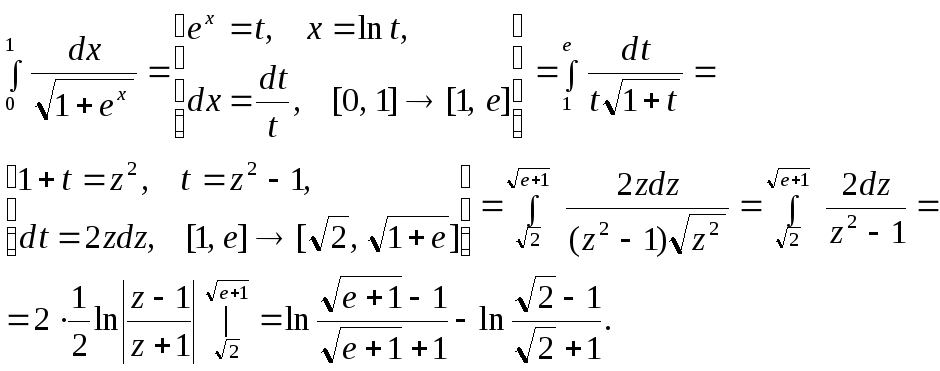
В этих примерах мы заменяли функцию некоторой пере -менной. Теперь рассмотрим случаи подстановки.

4.

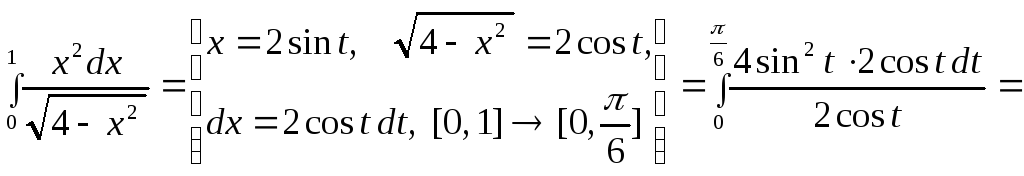
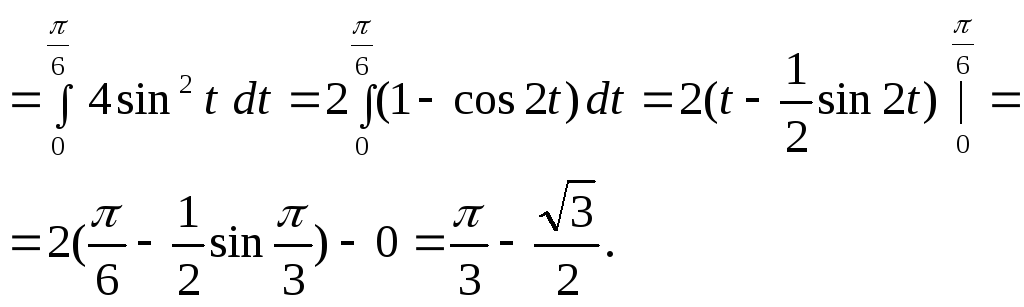
5.

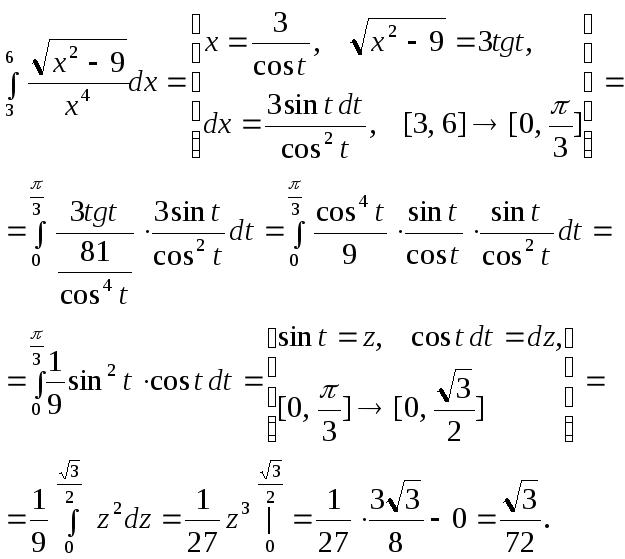
3. Интегрирование «по частям» в определённом интеграле.

Если функции иимеют непрерывные произ – водные на отрезке, то справедлива формула:

.

Правила выбора замены функций через итакие же, как для неопределённого интеграла.

Рассмотрим несколько примеров:

1.

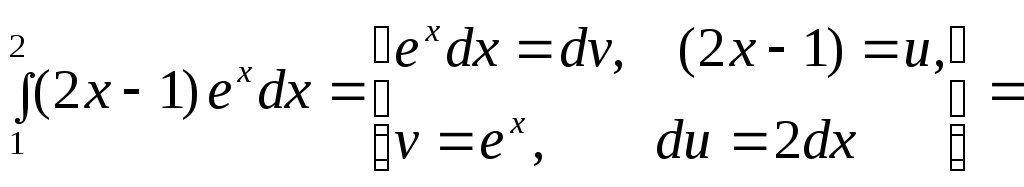
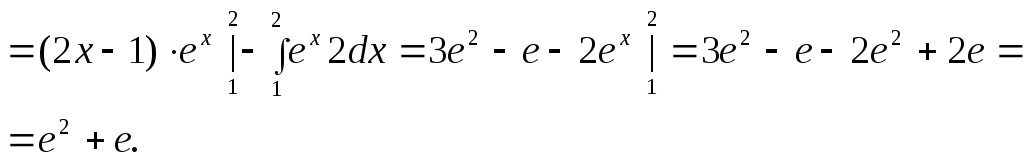
2.

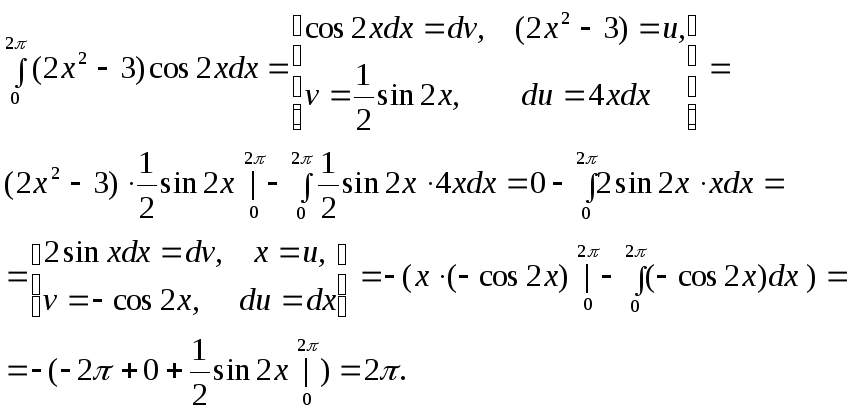
3.