§ 9. Экстремум функции двух переменных.

Пусть функция определена в некоторой окрестноститочки.

Определение 1. Говорят, что функция имеет в точкелокальный максимум, если существует какая окрестность этой точки , что для всех точеквыполняется неравенство

(1)

Если, при тех же условиях выполняется противоположное неравенство то говорят, что в точке функция имеетлокальный минимум. Точки локального максимума и минимума называются точками экстремума.

Из определения следует, что если функция имеет экстремум в точке, то в окрестности точки полное приращение функции

имеет вполне определённый знак, а именно, в окрест -ности точки максимума ив окрестности точки миниму –ма.

Необходимое условие экстремума.

Если функция имеет экстремум в точкеи имеет в некоторой окрестности этой точки частные производные первого порядка, то эти производные обращаются в ноль в точке, т.е.

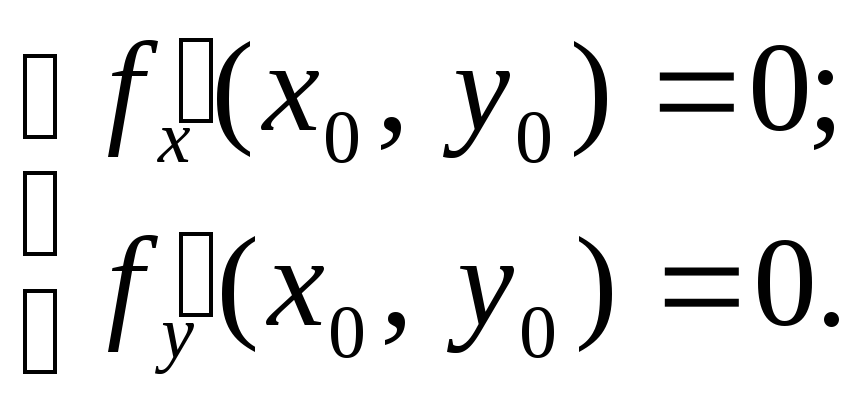
(2)

Точки, в которых выполняются условия (2), называются

стационарными точками, или точками возможного экстремума.

Другими словами, условия (2) не достаточны для существова -ния экстремума в точке .

Достаточное условие экстремума..

Пусть - стационарная точка, т.е. для неё выполнены условия (2). Пусть, далее в некоторой окрестности этой точки функцияимеет частные производные второго порядка, непрерывные в точкеПусть

.

Положим:

. (3)

Если , то функция имеет экстремум в точке, причём, если, то минимум, если- максимум; если, то в точкефункция не имеет экст- ремума; если, то признак ответа не лаёт и необходимо дальнейшее исследование.

ПРИМЕРЫ: Найти экстремумы следующих функций:

1. .

Найдём стационарные точки:

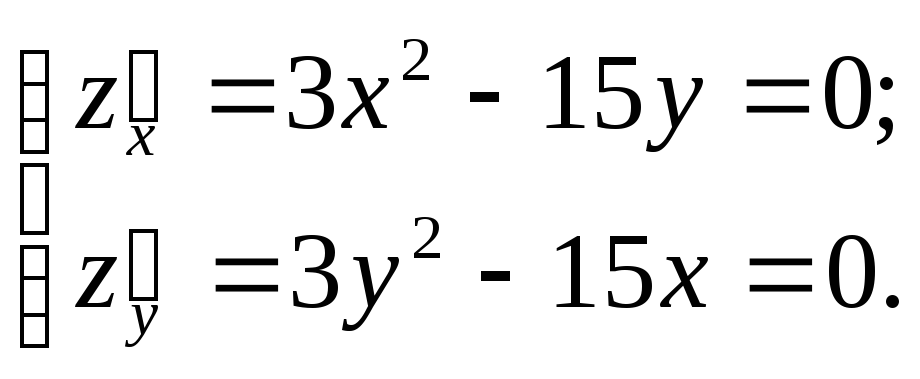Тогда

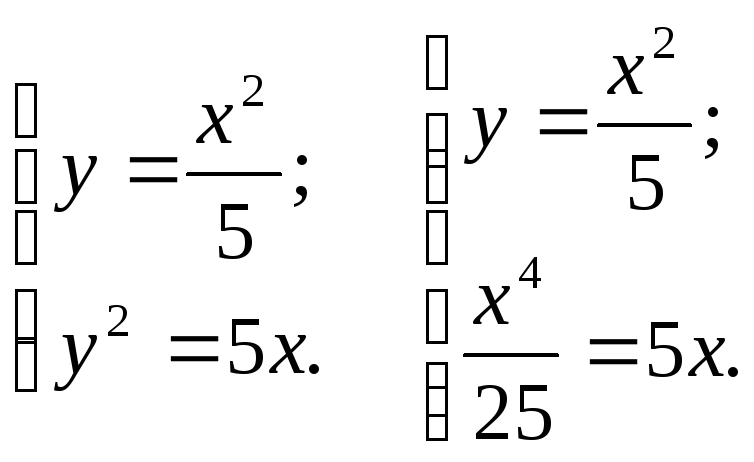
Решаем второе уравнение: , или

Тогда

Исследуем обе точки на экстремум, пользуясь достаточным условием экстремума. Для этого найдём вторые производные:

Для точки Тогда, по формуле (3),и в этой точке нет экстремума функции.

Для точки Тогда

и в этой точке функция имеет экстремум, причём, так как , то в точкефункция имеет минимум и

2.

Ищем стационарные точки:

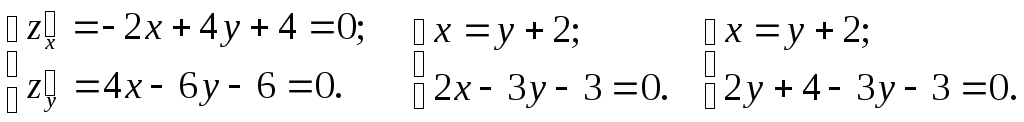
Тогда - стационарная точка. Исследуем эту точку на экстремум по достаточному признаку:Следовательно, в точкефункция имеет экстремум, причём, так как, то максимум.

§ 10. Наибольшее и наименьшее значение

ФУНКЦИИ В ЗАМКНУТОЙ ОБЛАСТИ.

Пусть функция определена и непрерывна в не- которой замкнутой областина плоскости. Тогда наибольшее и наименьшее значение в этой области функция может прини- мать либо в стационарных точках, попадающих в область, ли -бо на границе области. Правила нахождения наибольшего и наименьшего значения лучше рассмотреть на примерах.

ПРИМЕРЫ. Найти наибольшее и наименьшее значение функции в замкнутой области.

1.

С 3

2

-1 0 2 3

-1 К А

Сначала найдём стационарную точку:

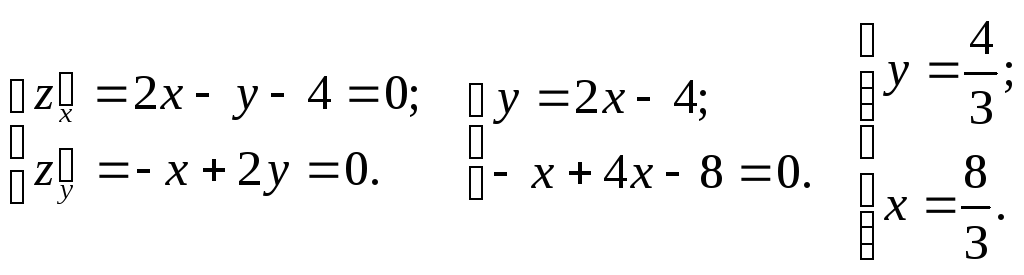
Точка не попадает в область. Найдём критические точки на границе области. На участкеТогда

Точка лежит на отрезке границы области. На участке. Тогда

Точка На третьем участке , тогда

Точка .

Таким образом мы нашли три точки, в которых функция мо -жет принять экстремальные значения. Кроме того необходимо ещё учесть угловые точки ,. В каждой из этих точек найдём значение функции:

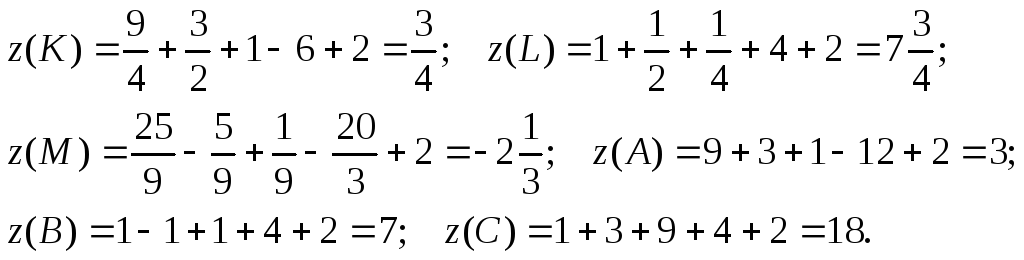Итак, наибольшее значение функции в области :Наименьшее значение функции в области:

2.

4 С

-3 -2 2 3

-5

Найдём стационарные точки:

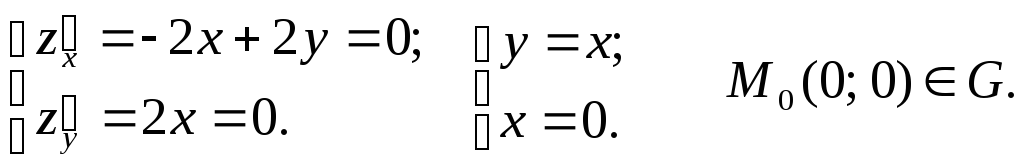
Найдём критические точки на границе области Точка

На участке

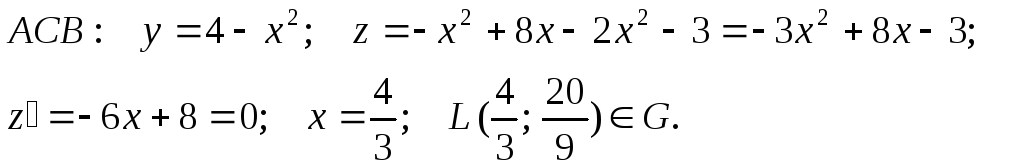
Кроме того, нужно ещё рассмотреть угловые точки:

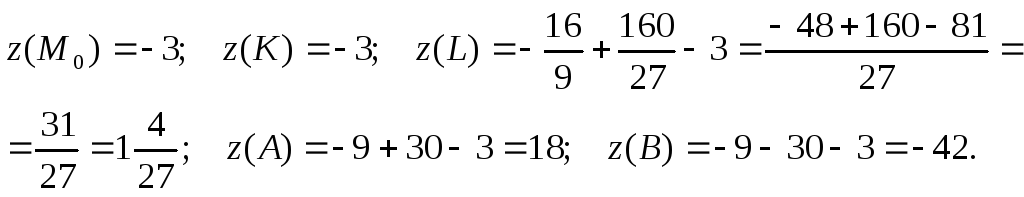
Таким образом, самое большое значение функция принимает в точке; самое маленькое значение- в точке.

4. КРАТНЫЕ ТНТЕГРАЛЫ.