9 Уравнения Лагранжа (второго рода)

Как отмечалось выше, задача о движении механической системы из частиц сголономными связями сводится к системескалярных уравнений снеизвестными, дополняя которуюнезависимыми соотношениями между координатами частиц и реакциями связей, можно получить решаемую системууравнений Лагранжа первого рода.

Метод обобщенных координат позволяет заменить систему 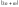скалярных уравнений вида (2.1.10) системой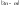дифференциальных уравнений в независимых обобщенных координатах, не содержащих явно сил реакцийи называемыхуравнениями Лагранжа второго рода (или просто уравнениями Лагранжа). Эти уравнения позволяют найти закон движения системы частиц, а затем с помощью (2.1.10) можно определить неизвестные реакции связей. Уравнения Лагранжа имеют инвариантную скалярную форму во всех СК, что позволяет составлять уравнения в наиболее удобной СК, не пользуясь громоздкими формулами перехода.

Для механической системы с идеальными связями задача математически заключается в преобразовании к обобщенным координатам общего уравнения механики

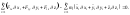(2.4.1)

Используя соотношения (2.3.1), выражающие декартовы координаты частиц системы через обобщенные координаты, а также понятие обобщенной силы (2.3.6), из (2.4.1) с помощью довольно громоздких преобразований (см. подробнее в [4, с. 181–182]) получим

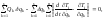(2.4.2)

где 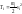– кинетическая энергия отдельной частицы,–обобщенные скорости. Кинетическая энергия системы частиц 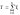, тогда

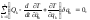(2.4.3) и

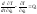, . (2.4.4)

Это и есть искомые уравнения Лагранжа. Для их составления необходимо знать выражение для кинетической энергии системы частиц в выбранных обобщенных координатах и значения обобщенных сил. Каждой обобщенной координате соответствует свое уравнение Лагранжа.

Особый интерес представляют уравнения Лагранжа, описывающие движение системы частиц с обобщенно-потенциальными силами. Сила называется обобщенно-потенциальной, если она зависит от обобщенных координат, обобщенных скоростей, времени и удовлетворяет условию:

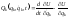,, (2.4.5)

где 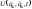–обобщенно-потенциальная функция (обобщенный потенциал). Подставляя (2.4.5) в (2.4.4), находим:

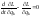, , (2.4.6)

где 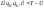–функция Лагранжа (лагранжиан). Уравнения (2.4.6) справедливы также, если 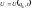– потенциальная функция, или если– потенциальная энергия (частный случай консервативных сил).

Итак, для составления уравнений Лагранжа в случае обобщенно-потен-циальных сил достаточно знать выражение для лагранжиана системы частиц. При этом уравнения (2.4.6) инвариантны по отношению к выбору системы отсчета. Лагранжиан задается неоднозначно: добавление к нему любой величины, не зависящей явно от 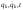, не изменяет уравнений (2.4.6).

При наличии диссипативных сил уравнения Лагранжа принимают вид:

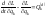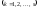, . (2.4.7)

Заметим, что если диссипативные силы линейно зависят от скоростей частиц, то они могут быть выражены (см. подробнее в []) через скалярную функцию:

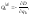(2.4.8)

где 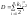–диссипативная функция Рэлея.