7 Принципы д¢Аламбера, виртуальных перемещений и

д¢Аламбера-Лагранжа. Общее уравнение механики

Д¢Аламбер показал, что дифференциальные уравнения движения системы частиц могут быть представлены в форме уравнений равновесия системы сил. Уравнения движение для системы из n частиц имеют вид:

, i = 1, 2, …, n (2.2.1)

Назовем векторы

(2.2.2)

д¢Аламберовыми силами инерции. Тогда

(2.2.3)

т. е. дифференциальные уравнения движения приняли вид условий равновесия сил, приложенных к частицам системы.

Принцип д¢Аламбера: если к заданным силам и реакциям связей добавить силы, равные силам инерции, то полученная система будет находиться в равновесии.

Математическое выражение принципа д¢Аламбера в декартовых координатах:

(2.2.4)

Принцип д¢Аламбера открывает возможность применения к решению динамических задач специфических методов аналитической статики, что в ряде случаев упрощает решение.

Введем понятия возможных, действительных и виртуальных перемещений. Возможным перемещением называют обычно бесконечно малое перемещение частицы, совместимое с наложенными связями, т. е. удовлетворяющее уравнению связи

(2.2.5)

Действительное перемещение – то из возможных, которое удовлетворяет уравнениям движения. Если возможное перемещение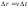(и– элементарно малые величины), то из известного дифференциального уравнения связидля возможного перемещения получаем:

(2.2.6)

Виртуальным перемещением 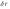называют бесконечно малое «перемещение» частицы, допускаемое связью в данный фиксированный момент времени. По сути это разность двух бесконечно близких возможных перемещений:

(2.2.7)

Подставляя в (2.2.6), находим:

(2.2.8)

что совпадает с (2.2.6) при стационарной связи ( т. е. при ) Таким образом, при стационарных связях понятия виртуального и возможного перемещений совпадают. Виртуальное перемещение не обусловлено действием сил и не обладает длительностью – это чисто геометрическое понятие, характеризующее структуру наложенных связей.

В математике величины вида называютвариациями; – вариация радиус-вектора частицы, причем

(2.2.9)

Вариация координаты – её бесконечно малое приращение, обусловленное переходом в данный момент времени от заданного движения к мысленному, допускаемому связями. Вариация отличается от бесконечно малого приращения координаты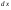, обусловленного приращением аргумента (времени):И вариация, и дифференциал – бесконечно малые изменения координаты, различные по своей природе.

В аналитической механике широко применяется метод варьирования как координат, так и функций координат частиц механической системы. Пусть имеется функция координат и времени

(2.2.10)

Если координаты подверглись варьированию, то новое значение функции

(2.2.11)

Разложим (2.2.11) в ряд Тейлора по степеням бесконечно малых величин :

(2.2.12)

Вариация функции (т. е. её приращение, обусловленное варьированием независимых аргументов)

(2.2.13)

отличается от полного дифференциала отсутствием члена с .

Т. к. координаты частицы до и после перемещения должны удовлетворять уравнениям связей, то их вариации не могут быть совершенно произвольными независимыми величинами. В самом деле, если уравнение связи

(2.2.14)

то должно выполняться равенство

(2.2.15)

Тогда

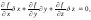(2.2.16)

т. е. одна из вариаций координат оказывается зависимой.

Все сказанное выше применимо, естественно, и для системы частиц, для которой среди вариаций координат тольконезависимых вариаций (столько, сколько степеней свободы).

Вернемся к рассмотрению системы из частиц. Для её равновесия необходимо и достаточно, чтобы алгебраические суммы проекций всех сил, приложенных к каждой частице, на каждую координату были равны нулю:

(2.2.17)

Здесь – равнодействующая активных сил, приложенных к-й частице,– равнодействующая соответствующих реакций связей,Домножим уравнение (2.2.17) на вариации соответствующих координат и просуммируем:

(2.2.18)

Выражения вида иимеют смысл работы на виртуальных перемещениях и называютсявиртуальной работой. Итак, сумма виртуальных работ заданных (активных) сил и сил реакции для всех частиц системы, находящейся в равновесии, равна нулю.

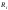Заметим, что введя в уравнение реакции связей, мы от системы частиц со связями перешли к системе с силами и(принцип освобождаемости от связей). При таком подходе все вариациинезависимы, и уравнения (2.2.17) и (2.2.18) эквивалентны.

Заметим также, что , где– силы нормальных реакций, не совершающие работы. Тогда

(2.2.19)

Если связи идеальные, то (в общем случае идеальными можно называть связи, для которых виртуальная работа сил реакции обращается в нуль). В этом случае

(2.2.20)

(2.2.20) – условие Лагранжа, выражающее принцип виртуальных перемещений: виртуальная работа заданных сил, приложенных к системе с идеальными связями и находящейся в равновесии, равна нулю.

Объединим принцип виртуальных перемещений с принципом д¢Аламбера. Для идеальных связей запишем:

(2.2.21)

Это общее уравнение механики. В любой момент времени движения механической системы с идеальными связями алгебраическая сумма виртуальных работ заданных сил и д¢Аламберовых сил инерции равна нулю – объединенный принцип д¢Аламбера–Лагранжа, который можно использовать как основную аксиому механики.

В декартовых координатах общее уравнение механики:

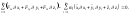(2.2.22)

Общее уравнение механики легко обобщается на случай неидеальных связей:

(2.2.23)