
- •2 Преобразования кинематических характеристик частицы при
- •3 Динамические характеристики частицы. Законы Ньютона
- •4 Принцип относительности Галилея. Механическая концепция
- •5 Уравнение движения частицы относительно исо. Принцип
- •6 Уравнение движения частицы относительно нисо. Силы
- •7 Принципы д¢Аламбера, виртуальных перемещений и
- •8 Обобщенные координаты и обобщенные силы
- •9 Уравнения Лагранжа (второго рода)
- •10 Принцип экстремального действия. Преимущество
- •11 Обобщенная энергия, обобщенный импульс и законы их
- •12 Центр инерции и законы сохранения импульса и момента
- •13 Связь законов сохранения со свойствами симметрии
- •14 Задача двух тел. Движение в центральном поле
- •15 . Задача Кеплера
- •16 Рассеяние частиц. Формула Резерфорда
- •17 Свободные и вынужденные одномерные колебания
- •18 Затухающие колебания
- •19 Вынужденные колебания при наличии трения
- •20 Кинематическое описание твердого тела. Углы Эйлера
- •21 Кинетическая энергия и момент импульса твердого тела
- •22 Уравнения движения твердого тела. Динамические уравнения Эйлера
- •23 Функция Гамильтона и канонические уравнения Гамильтона
- •24 Уравнение Гамильтона-Якоби. Теорема Якоби
- •25 Тензоры деформации и скоростей деформации
- •26 Закон сохранения массы и уравнение непрерывности
- •27 Поле скоростей и его характеристики
- •28 Силы, действующие в сплошных средах. Тензор напряжения
- •29 Необходимые уравнения движения сплошных сред
- •30 Уравнения движения идеальной жидкости
- •31 Интегралы уравнений движения идеальной жидкости
- •32 Звуковые волны
6 Уравнение движения частицы относительно нисо. Силы
инерции. Принцип эквивалентности сил инерции и гравитации
Основное уравнение
динамики записано выше для инерциальной
системы отсчета (ИСО). В общем случае
система координат может быть связана
с телом отсчета, движущимся произвольно
в некоторой ИСО. Для записи уравнения
движения частицы относительно такой
неинерциальной системы отсчета (НИСО)
воспользуемся формулой сложения
ускорений (теоремой Кориолиса):
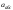 =
= +
+ +
+ .
Умножая это равенство на массу частицы
и учитывая, что
.
Умножая это равенство на массу частицы
и учитывая, что –
ускорение частицы в ИСО (
–
ускорение частицы в ИСО ( =
= ),
получим:
),
получим:
 =
=
 +(
+( )+(
)+( ).
(1.8.1)
).
(1.8.1)
Здесь сила
 выражает действие на частицу других
тел и полей и может быть указана в виде
функции координат, скорости и времени:
выражает действие на частицу других
тел и полей и может быть указана в виде
функции координат, скорости и времени: .
Движение же НИСО проявилось в (1.8.1) через
слагаемые
.
Движение же НИСО проявилось в (1.8.1) через
слагаемые =
= и
и =
=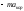 .
Эти слагаемые кинематически в НИСО не
могут быть обнаружены и интерпретируются
как силы, приложенные к частице и
вызывающие ее ускорение относительно
НИСО. Таким образом, чтобы сохранить
для частицы в НИСО традиционную форму
основного уравнения динамики, величины
.
Эти слагаемые кинематически в НИСО не
могут быть обнаружены и интерпретируются
как силы, приложенные к частице и
вызывающие ее ускорение относительно
НИСО. Таким образом, чтобы сохранить
для частицы в НИСО традиционную форму
основного уравнения динамики, величины и
и следует рассматривать как особого рода
силы –силы
инерции,
которые не являются результатом действия
каких-либо тел или полей на частицу, а
представляют прямой результат
неинерциальности системы отсчета.
следует рассматривать как особого рода
силы –силы
инерции,
которые не являются результатом действия
каких-либо тел или полей на частицу, а
представляют прямой результат
неинерциальности системы отсчета.
Итак, уравнение движения в НИСО имеет вид:
 =
=
 +
+ +
+ .
(1.8.2)
.
(1.8.2)
Здесь
 –
равнодействующая всех «ньютоновских»
сил, действующих на частицу,
–
равнодействующая всех «ньютоновских»
сил, действующих на частицу, –переносная
сила инерции,
–переносная
сила инерции,
 –кориолисова
сила инерции
(или просто сила
Кориолиса).
В общем случае
–кориолисова
сила инерции
(или просто сила
Кориолиса).
В общем случае
 =
= +
+ +
+ =
=

 ,
где
,
где –
переносное поступательное ускорение,
–
переносное поступательное ускорение, – переносное вращательное ускорение,
– переносное вращательное ускорение,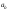 =
= =
= –
переносное центростремительное
ускорение;
–
переносное центростремительное
ускорение; ,
, и
и –поступательная,
вращательная и центробежная силы
инерции.
–поступательная,
вращательная и центробежная силы
инерции.
Если частица в
НИСО неподвижна, то
 =
0,
=
0, =
0 и
=
0 и +
+ =
0. Именно такое уравнение следует
применять к покоящемуся на Земле телу,
причем
=
0. Именно такое уравнение следует
применять к покоящемуся на Земле телу,
причем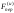
 .
.
Сила Кориолиса
зависит не только от переносного
движения, но и от относительного движения
частицы в НИСО:
 =
= =
= =
= .
На покоящиеся в НИСО тела сила Кориолиса
не действует.
.
На покоящиеся в НИСО тела сила Кориолиса
не действует.
Для тел на Земле центробежная сила инерции проявляется в зависимости ускорения свободного падения от широты местности (на экваторе величина g меньше, чем на полюсах). Сила Кориолиса отклоняет движущиеся тела (в северном полушарии любая река больше подмывает правый берег); действием силы Кориолиса объясняется своеобразное движение маятника Фуко. Совместное действие центробежной силы и силы Кориолиса отклоняет свободно падающее тело на юго-восток (в Северном полушарии) от направления к центру Земли.
Силы инерции, действующие на частицу в НИСО, по своим проявлениям не отличаются от фундаментальной силы, действующей в гравитационном поле. Это их свойство обусловлено пропорциональностью (при принятом выборе единиц измерения – равенством) инертной и гравитационной масс тела. Эта пропорциональность (равенство) для всех тел не вытекает из каких-либо положений механики, а является самостоятельным утверждением – обобщением экспериментальных фактов (опыты Галилея, Ньютона, Бесселя, Дикке, Панова и Брагинского и др.). Равенство проверено экспериментально с очень высокой степенью точности.
Важнейшим следствием равенства инертной и гравитационной масс является равенство ускорений для всех тел (частиц) в данной точке гравитационного поля (ускорение не зависит от массы рассматриваемого тела). Также не зависят от массы и ускорения, вызываемые заданными силами инерции. Это приводит к утверждению о неразличимости сил инерции и сил тяготения в небольшой области пространства за небольшие промежутки времени. Данное утверждение носит название принципа эквивалентности сил инерции и гравитации: поле тяготения в небольшой области пространства и времени по своему действию тождественно действию сил инерции в ускоренной системе отсчета. Заметим, что в небольшой области пространства и времени гравитационное поле можно считать однородным и стационарным.
Принцип эквивалентности сыграл фундаментальную эвристическую роль в создании общей теории относительности, в которой равноправными считаются все системы отсчета, а не только ИСО.
