31 Интегралы уравнений движения идеальной жидкости

Уравнения движения жидкости в общем виде не интегрируются. Для рассмотрения частного случая предположим:

1) жидкость идеальна, ее движение описывается уравнением Ламба-Громеки;

2) движение установившееся, т. е. переменные в уравнении движения не зависят от времени;

3) массовые силы потенциальные, т. е. ;

4) жидкость баротропна, т. е. .

При таких условиях уравнение Ламба-Громеки принимает вид:

. (9.2.1)

Умножая это уравнение скалярно на элементарное перемещение вдоль линии тока, для установившегося движения получим:

. (9.2.2)

Отсюда для данной линии тока имеем:

. (9.2.3)

Это интеграл Бернулли. Для различных линий тока значения постоянной разные.

При постоянной плотности в поле тяжести запишем:

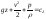,или. (9.2.4)

Смысл интеграла Бернулли в виде (9.2.4) выражает теорема Бернулли: сумма высот геометрической, скоростной и пьезометрической вдоль линии тока остается величиной неизменной.

Если жидкость покоится, то . Величина– пьезометрический напор.

Рассмотрим другой интеграл уравнений движения жидкости в предположениях:

1) жидкость идеальна;

2) движение потенциально, т. е. и;

3) жидкость баротропна, т. е. .

Тогда уравнение Ламба-Громеки запишем в виде:

. (9.2.5)

Легко видеть, что движение в рассматриваемом случае возможно, если силы потенциальные:,. (9.2.6)

Из (9.2.6) получаем интеграл Коши:. (9.2.7)

При этом уравнение непрерывности

, (9.2.8)

и уравнение состояния

. (9.2.9)

Итак, имеем систему из трех уравнений с неизвестными ,,р.

Пусть одновременно выполняются условия интегралов Бернулли и Коши:

1) жидкость идеальна;

2) движение установившееся;

3) движение потенциально

4) жидкость баротропна;

5) внешние силы потенциальны.

Тогда из уравнения Ламба-Громеки получаем интеграл Бернулли-Эйлера:

, (9.2.10) где

. (9.2.11)

Добавляя уравнение состояния вида (9.2.9) и уравнение непрерывности

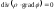, (9.2.12)

получаем систему уравнений для определения ,,р.

Если к условиям существования интеграла Бернулли-Эйлера добавить условие несжимаемости жидкости, то

; (9.2.13) для поля тяжести

. (9.2.14)

Для потенциальных движений несжимаемой жидкости уравнение непрерывности превращается в уравнение Лапласа:

, (9.2.15)

которое служит для определения при заданных граничных условиях.

32 Звуковые волны

Типичные случаи нестационарных течений жидкости – волновые движения, для которых характерны колебания отдельных частиц. Например, волны на поверхности жидкости, возникающие в результате того, что поверхность выведена из равновесия и колеблется под действием сил тяжести (такие волны принято называть гравитационными). При их изучении сжимаемость и вязкость не играют существенной роли, поэтому гравитационные волны описываются уравнениями нестационарных течений идеальной несжимаемой жидкости.

Упругими называют волны, возникающие во всей толще сжимаемой жидкости в результате расширения и сжатия ее частиц. Эти волны обусловлены упругими свойствами жидкости. Их частный случай – звуковые волны – малые колебательные движения, распространяющиеся в жидкости, вызванные попеременными малыми сжатиями и разрежениями.

Рассмотрим вопрос о волнах в жидкости, исходя из уравнений, описывающих ее движение. Упрощения:

1) массовых сил нет ();

2) движения потенциальны ();

3) скорости частиц жидкости малы (малые колебания);

4) изменения скорости при переходе от одной точки пространства к другой малы (т. е. малы величины типа , а также величина);

5) давление и плотность изменяются в малых пределах: ,, гдеи– давление и плотность для невозмущенной жидкости, и– малые добавки, зависящие от t и x, y, z. Тогда уравнение Эйлера:

(9.6.1)

Считая постоянными и, а также, получаем:

, (9.6.2) откуда

, (9.6.3)

где – произвольная функция времени. Поскольку потенциал определен с точностью до произвольной функции времени, уравнение движения звуковой волны (9.6.3) можно записать в виде:

. (9.6.4)

К этому уравнению добавим уравнение непрерывности:

. (9.6.5)

Учитывая, что ,– величина второго порядка малости, получим:(9.6.6)или. (9.6.7)

В (9.6.4) и (9.6.7) неизвестные . Добавим к этим уравнениям уравнение состояния - уравнение Пуассона, т. к. движение идеальной жидкости представляет собой адиабатический процесс:

или . (9.6.8)

Производя преобразования (см. подробнее в [1, с. 227]), находим:

. (9.6.9)

Уравнения (9.6.4), (9.6.7), (9.6.9) полностью описывают движение звуковых волн. Из них получаем волновое уравнение:

. (9.6.10)

Волновому уравнению удовлетворяют и другие переменные (и). Задача о распространении звуковой волны сводится к интегрированию этого уравнения.

Если рассматриваемые величины зависят только от t и х, то волна называется плоской. Волновое уравнение в этом случае:

. (9.6.11)

Интегрируя это уравнение с помощью метода характеристик (см. подробнее в [1, с. 228]), получаем:

, (9.6.12)

где и– произвольные функции. Изменения давления, плотности и скорости в плоской волне описываются такими же функциями, что и потенциал скорости. Например,

; (9.6.13)

при имеем. Если при этом, то плотность жидкости неизменна (а также неизменны давление, скорость, потенциал скорости). Значит, если в начальный момент времени плотность жидкости в точке 0 имела определенное значение, то такое же значение спустя времяt будет иметь плотность в точке на расстоянии ct от исходной вдоль оси 0х. Картина движения распространяется в жидкости вдоль оси 0х со скоростью звука с. Говорят, что функция представляет собой плоскую бегущую волну, распространяющуюся в положительном направлении оси 0х (– в противоположном направлении).

Если потенциал скорости 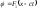, то скорость. Тогда,, т. е. скорость частицы много меньше скорости звука.

Скорость распространения волны определяется формулой Лапласа:

, (9.6.14)

что хорошо согласуется с экспериментальным значением скорости звука в воздухе.