
- •2 Преобразования кинематических характеристик частицы при
- •3 Динамические характеристики частицы. Законы Ньютона
- •4 Принцип относительности Галилея. Механическая концепция
- •5 Уравнение движения частицы относительно исо. Принцип
- •6 Уравнение движения частицы относительно нисо. Силы
- •7 Принципы д¢Аламбера, виртуальных перемещений и
- •8 Обобщенные координаты и обобщенные силы
- •9 Уравнения Лагранжа (второго рода)
- •10 Принцип экстремального действия. Преимущество
- •11 Обобщенная энергия, обобщенный импульс и законы их
- •12 Центр инерции и законы сохранения импульса и момента
- •13 Связь законов сохранения со свойствами симметрии
- •14 Задача двух тел. Движение в центральном поле
- •15 . Задача Кеплера
- •16 Рассеяние частиц. Формула Резерфорда
- •17 Свободные и вынужденные одномерные колебания
- •18 Затухающие колебания
- •19 Вынужденные колебания при наличии трения
- •20 Кинематическое описание твердого тела. Углы Эйлера
- •21 Кинетическая энергия и момент импульса твердого тела
- •22 Уравнения движения твердого тела. Динамические уравнения Эйлера
- •23 Функция Гамильтона и канонические уравнения Гамильтона
- •24 Уравнение Гамильтона-Якоби. Теорема Якоби
- •25 Тензоры деформации и скоростей деформации
- •26 Закон сохранения массы и уравнение непрерывности
- •27 Поле скоростей и его характеристики
- •28 Силы, действующие в сплошных средах. Тензор напряжения
- •29 Необходимые уравнения движения сплошных сред
- •30 Уравнения движения идеальной жидкости
- •31 Интегралы уравнений движения идеальной жидкости
- •32 Звуковые волны
28 Силы, действующие в сплошных средах. Тензор напряжения
Выделим в сплошной
среде объем V,
ограниченный поверхностью
 .
Все силы, действующие на выделенную
часть сплошной среды, можно разделить
на два класса.
.
Все силы, действующие на выделенную
часть сплошной среды, можно разделить
на два класса.
Массовые силы
–
силы, действующие на каждый элемент
объема dV
независимо от того, существуют ли рядом
с ним другие части среды (например, силы
тяготения). Если
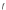 –
массовая сила в расчете на единицу
массы, то на объем dV
с массой
–
массовая сила в расчете на единицу
массы, то на объем dV
с массой
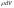 действует массовая сила
действует массовая сила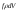 ;
главный вектор этих сил
;
главный вектор этих сил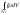 .
.
Поверхностные
силы –
силы взаимодействия между отдельными
частями сплошной среды. Внутри выделенного
объема V
эти силы и их моменты уравновешиваются
в соответствии с III
законом Ньютона, т. е. эти силы остаются
приложенными лишь к поверхностным
частям объема V
(к поверхности
 ).
Поверхностную силу, действующую на
единицу площади, ориентация которой в
пространстве задана внешней нормалью
).
Поверхностную силу, действующую на
единицу площади, ориентация которой в
пространстве задана внешней нормалью ,
обозначают
,
обозначают и называют напряжением сил на
рассматриваемом элементе поверхности.
На элемент поверхности
и называют напряжением сил на
рассматриваемом элементе поверхности.
На элемент поверхности действует поверхностная сила
действует поверхностная сила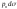 ;
главный вектор поверхностных сил,
действующих на объемV,
равен
;
главный вектор поверхностных сил,
действующих на объемV,
равен
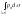 .
Проекция
.
Проекция на
на –
нормальное
напряжение
(или нормальное
давление),
проекция
–
нормальное
напряжение
(или нормальное
давление),
проекция
 на площадку, к которой
на площадку, к которой приложено–
сдвигающее
(касательное)
напряжение.
приложено–
сдвигающее
(касательное)
напряжение.
Выделим мысленно
в среде элементарную треугольную
пирамиду, три грани которой параллельны
координатным плоскостям, т. е. внешние
нормали к этим граням направлены
противоположно осям 0x,
0y,
0z
декартовой СК. Внешняя нормаль
 к четвертой грани составляет с этими
осями углы, косинусы которых обозначим
к четвертой грани составляет с этими
осями углы, косинусы которых обозначим .
Если площадь этой грани равна
.
Если площадь этой грани равна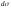 ,
то площади остальных граней равны
,
то площади остальных граней равны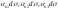 .
Пусть объем пирамидыdV.
Тогда на нее действуют массовые силы
.
Пусть объем пирамидыdV.
Тогда на нее действуют массовые силы
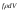 ,
а массовые силы инерции равны
,
а массовые силы инерции равны ,
где
,
где –
ускорение пирамиды. Поверхностные
силы, действующие на грани пирамиды,
равны:
–
ускорение пирамиды. Поверхностные
силы, действующие на грани пирамиды,
равны:
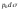 ,
,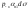 ,
, ,
,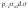 .
Условие равновесия пирамиды:
.
Условие равновесия пирамиды:
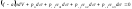 .
(8.6.1)
.
(8.6.1)
Объем
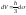 ,
гдеh
–
высота пирамиды. Тогда
,
гдеh
–
высота пирамиды. Тогда
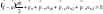 ,
(8.6.2) и при
,
(8.6.2) и при
 имеем:
имеем:
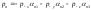 ,
(8.6.3)
,
(8.6.3)
Величина вида
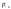 определяет воздействие на соответствующую
грань частиц среды, находящихся вне
пирамиды. На эти частицы со стороны
пирамиды действует сила
определяет воздействие на соответствующую
грань частиц среды, находящихся вне
пирамиды. На эти частицы со стороны
пирамиды действует сила .
Тогда напряжение
.
Тогда напряжение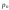 при произвольной ориентации внешней
нормали может быть определено, если
известны напряжения в той же точке для
площадок, внешние нормали которых
сонаправлены с осями координат 0x,
0y,
0z:
при произвольной ориентации внешней
нормали может быть определено, если
известны напряжения в той же точке для
площадок, внешние нормали которых
сонаправлены с осями координат 0x,
0y,
0z:
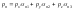 .
(8.6.4)
.
(8.6.4)
Проецируя (8.6.4) на координатные оси, получим:
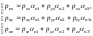 (8.6.5)Здесь
(8.6.5)Здесь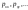 –
компоненты
напряжения.
Пусть
–
компоненты
напряжения.
Пусть
 –
проекция
–
проекция
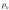 на произвольное направление
на произвольное направление ,
характеризуемое направляющими косинусами
,
характеризуемое направляющими косинусами .
Тогда
.
Тогда
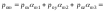

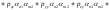
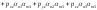 .
(8.6.5)
.
(8.6.5)
Проделав то же самое, что и при получении тензора деформации, получим тензор напряжения:
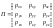 .
(8.6.6)
.
(8.6.6)
Тензор симметричный,
т. е.
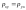 ,
, ,
, .
Итак, напряжение в данной точке–
функция 6 величин:
.
Итак, напряжение в данной точке–
функция 6 величин:
 ,
,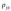 ,
,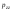 ,
,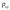 ,
,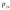 ,
, .
.
Существуют три взаимно перпендикулярные оси, для которых
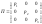 .
(8.6.7)
.
(8.6.7)
Здесь
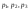 –
главные напряжения.
–
главные напряжения.
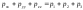 ,
(8.6.8)
,
(8.6.8)
т. е. сумма нормальных напряжений на три взаимно перпендикулярные площадки не зависит от ориентации последних.
Заметим, что компоненты напряжения выражаются в переменных Эйлера, т. е. являются функциями переменных x, y, z, t.
