24 Уравнение Гамильтона-Якоби. Теорема Якоби

Наряду с обыкновенными дифференциальными уравнениями Лагранжа и Гамильтона, существует уравнение в частных производных, описывающее движение механической системы в поле обобщенно-потенциальных сил при наличии голономных идеальных связей – уравнение Гамильтона-Якоби. Ранее было показано, что,k = 1, 2, ..., s, (7.6.1)

и . Заменяя в (7.6.1) импульсы производными от действия по координатам, получаемуравнение Гамильтона-Якоби, которому удовлетворяет функция действия :

, k = 1, 2, ..., s, (7.6.2)

Уравнение Гамильтона-Якоби также служит основой для некоторого общего метода интегрирования уравнений движения.

Как известно, всякое дифференциальное уравнение в частных производных первого порядка имеет решение, зависящее от произвольной функции – так называемый общий интеграл уравнения. В механических применениях основную роль играет, однако, не общий интеграл уравнения Гамильтона-Якоби, а полный интеграл – решение дифференциального уравнения в частных производных, содержащее столько независимых произвольных постоянных, сколько независимых переменных в уравнении.

В уравнении Гамильтона-Якоби независимые переменные . Для системы сs степенями свободы полный интеграл этого уравнения должен содержать (s + 1) произвольных постоянных. Поскольку функция S входит в уравнение только через свои производные, то одна из произвольных постоянных содержится в полном интеграле аддитивным образом, т. е. вид полного интеграла уравнения Гамильтона-Якоби:

, (7.6.3)

где – произвольные постоянные.

Для выяснения связи между полным интегралом уравнения Гамильтона-Якоби и решением уравнений движения произведем каноническое преобразование от величин ик новым переменным, причем функциювыберем в качестве производящей функции, а величины– в качестве новых импульсов. Новые координаты обозначим. Поскольку производящая функция зависит от старых координат и новых импульсов, используем формулы:

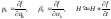(7.6.4)

Функция f удовлетворяет уравнению Гамильтона-Якоби, поэтому

, (7.6.5)

и канонические уравнения в новых переменных имеют вид:

, (7.6.6)

откуда. (7.6.7)

С другой стороны s уравнений дают возможность выразитьs координат через время и 2s постоянных и. Тем самым находится общий интеграл уравнения движения.

Изложенное выше обобщает теорема Якоби: если некоторая функция является полным интегралом уравнения Гамильтона-Якоби, то решение канонических уравнений Гамильтона определяется следующими соотношениями:

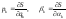, k = 1, 2, ..., s, (7.6.8)

где и– произвольные постоянные.

Первые соотношения (7.6.8) определяют обобщенные импульсы как функции координат и времени: 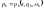; вторые соотношения (7.6.8) дают интегралы канонических уравнений вида, разрешая которые относительно, находим обобщенные импульсы как функции времени и 2s независимых постоянных: .

Используя теорему Якоби, можно решить задачу о движении механической системы с обобщенно-потенциальными силами и идеальными голономными связями следующим образом: по известной функции Гамильтона составляем уравнение Гамильтона-Якоби, а затем находим полный интеграл этого уравнения вида (7.6.3) с последующим использованием уравнений (7.6.8).

Если мы имеем неполный интеграл уравнения Гамильтона-Якоби, зависящий от числа произвольных постоянных меньше s, то, хотя с его помощью и нельзя найти общий интеграл уравнений движения, можно все же несколько упростить задачу его нахождения. Так, если известна функция S, содержащая одну произвольную постоянную , то соотношение

(7.6.9)

дает одно уравнение, связывающее .

Уравнение Гамильтона-Якоби упрощается для случая явной независимости H от t (например, для консервативной системы). Зависимость действия от времени сводится при этом к выражению

, (7.6.10)

и для укороченного действия уравнение Гамильтона-Якоби имеет вид:

, k = 1, 2, ..., s. (7.6.11)

Заметим, что физические допущения, лежащие в основе уравнений Гамильтона и уравнения Гамильтона-Якоби, одинаковы. Но основной метод решения уравнения Гамильтона-Якоби (метод разделения переменных) включает в себя как частный случай метод циклических координат Лагранжа, и при рассмотрении уравнения Гамильтона-Якоби наиболее естественно вскрывается достаточно глубокая аналогия между механикой частицы и волновым процессом, играющая важную роль при обсуждении волнового аспекта квантовомеханических явлений.