19 Вынужденные колебания при наличии трения

Задача решается аналогично изложенному в подразделе 5.1. Будем рассматривать также случай периодически изменяющейся вынуждающей силы. Уравнение движения имеет вид:

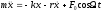(5.4.1)

(считаем начальную фазу равной нулю для вынуждающей силы). Тогда

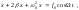(5.4.2)

где . Решая (5.4.2), получаем:

(5.4.3)

Постоянные инайдем, подставив второе слагаемое (5.4.3) в (5.4.2) и приравняв коэффициенты приив полученном уравнении:

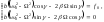(5.4.4)

Отсюда получаем:

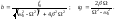(5.4.5)

При (в фиксировано для заданных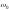,и) спустя достаточно большой промежуток времени имеют место установившиеся колебания

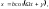(5.4.6)

Рисунок 5.4.1

поскольку первое слагаемое в (5.4.3) экспоненциально убывает с течением времени. График зависимости 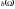представлен на рисунке 5.4.1.

Легко видеть, что при определенном значении 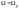амплитудадостигает максимума (имеет место явление резонанса). Найти резонансную частоту при заданных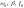несложно, исследовав функцию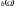на экстремум. Проделав эту операцию, получим: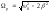(5.4.7) и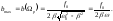(5.4.8)

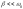
При 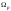отличается отлишь на величину второго порядка малости (но все же отличается!). Легко видеть, что с ростомпри заданной частотерезонансные частотаи амплитудауменьшаются.

Рассмотрим область частот вблизи резонанса при 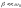. Пусть,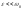. Тогда в (5.4.5) можно положить

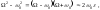(5.4.9)

а также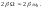(5.4.10)

Это дает: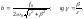(5.4.11)

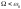
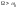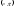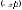Отметим характерную особенность хода изменения разности фаз между колебанием и вынуждающей силой при изменении частоты последней. Эта разность всегда отрицательна, т.е. колебание «запаздывает» относительно внешней силы. Вдали от резонанса пристремится к нулю, а при– к значению. Изменениеот 0 допроисходит в узкой (шириной ~) области частот, близких к; через значениеразность фаз проходит при. Отметим, что при(без трения) изменение фазы вынужденного колебания на величинупроисходит скачком при; учет трения «размазывает» этот скачок.

При установившемся движении (см. (5.4.6)) энергия системы остается неизменной, но система непрерывно поглощает энергию от внешнего источника и диссипирует ее за счет трения. Обозначим 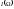количество энергии, поглощаемой в среднем в единицу времени, в зависимости от частоты внешней силы. Как уже отмечалось в предыдущем подразделе, по величине

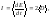(5.4.12)

где – диссипативная функция, определяемая для одномерного движения формулой (см. (5.3.23)):

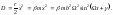(5.4.13)

Учитывая, что за период 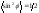, имеем:

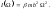(5.4.14)

Тогда вблизи резонанса, подставляя в (5.4.14) значение , получаем

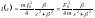(5.4.15)

Такой вид зависимости интенсивности поглощения энергии от частоты называется дисперсионным (рисунок 5.4.2). Полушириной резонансной кривой называют значение , при котором величина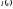уменьшается вдвое по сравнению с ее максимальным значением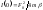при. Из (5.4.15) видно, что в данном случае эта полуширина равна, а высота максимума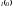~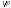. Таким образом, при уменьшении коэффициента затуханиярезонансная кривая становится все уже и выше (максимум более острый). Площадь же

под резонансной кривой неизменна:

(5.4.16)

Рисунок 5.4.2