17 Свободные и вынужденные одномерные колебания

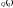Рассмотрим механическую систему с одной степенью свободы и исследуем ее малые колебания вблизи положения устойчивого равновесия. Система имеет только одну обобщенную координату . Пусть в положении равновесия. Тогда соответствующая координатеобобщенная силапри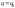обращается в нуль. Если сила потенциальная, то

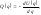(5.1.1) где – потенциальная энергия, имеющая экстремум в положении равновесия. При устойчивом равновеси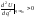ии.

При малом отклонении от положения равновесия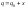, и потенциальная энергия

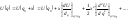(5.1.2)

Выбор нулевого состояния для произволен, поэтому можно положить

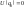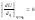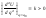. Равновесие при ,, т. е.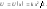(5.1.3)

Это означает, что на систему действует квазиупругая сила

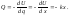(5.1.4)

Кинетическая энергия системы с одной степенью свободы

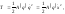(5.1.5)

где 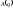– коэффициент инерции (постоянная или медленно меняющаяся функция). Для малых смещений можно считать. Подчеркнем, чтосовпадает с массой только в том случае, когда– декартова координата частицы, характеризующей (заменяющей) движущуюся систему.

Функция Лагранжа для системы, совершающей малые гармонические колебания (для одномерного гармонического осциллятора), имеет вид:

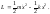(5.1.6)

Подставляя в уравнение Лагранжа 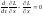, находим уравнение движения: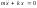(5.1.7) или

(5.1.8)

Общее решение уравнения (5.1.8) может быть представлено в виде

(5.1.9) или

(5.1.10)

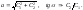Произвольные постоянные исвязаны с постояннымиисоотношениями:(5.1.11)

Итак, вблизи положения равновесия система совершает гармонические колебания с амплитудой , фазой 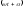;–начальное значение фазы, зависящее от выбора начала отсчета времени, –циклическая частота колебаний (в теоретической физике ее называют обычно просто частотой).

Частота – основная характеристика колебаний, не зависящая от начальных условий движения и всецело определяемая свойствами механической системы как таковой (см. (5.1.8)). Отметим, что это свойство частоты связано с малостью колебаний и исчезает при переходе к более высоким приближениям. С математической точки зрения это свойство связано с квадратичной зависимостью от.

Энергия системы при малых колебаниях

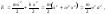(5.1.12)

т. е. энергия пропорциональна квадрату амплитуды.

Иногда удобно записывать зависимость 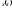в виде вещественной части комплексного выражения: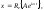(5.1.13) где–комплексная амплитуда. Записав ее в виде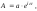(5.1.14)

вернемся к выражению (5.1.10). Модуль совпадает с обычной амплитудой, аргумент – с начальной фазой.

Перейдем к рассмотрению колебаний в системе, подверженной действию внешнего переменного поля; такие колебания называют вынужденными в отличие от рассмотренных выше свободных колебаний. Т. к. рассматриваются малые колебания, то и внешнее поле полагаем достаточно слабым (иначе оно могло бы вызывать большие ).

Итак, наряду с собственной потенциальной энергией 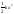необходимо рассматривать еще некоторое слагаемое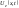, связанное с действием внешнего поля. При малыхимеем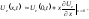(5.1.15)

Первое слагаемое в (5.1.15) можно не включать в выражение для лагранжиана (его можно рассматривать как полную производную по от некоторой другой функции времени). Во втором слагаемом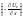есть внешняя «сила», действующая на систему в положении равновесия и являющаяся заданной функцией времени; обозначим ее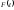. Тогда лагранжиан системы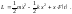(5.1.16)

Подставляя в уравнение Лагранжа, находим уравнение движения:

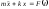(5.1.17)или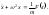(5.1.18)

Здесь – по-прежнему частота свободных колебаний.

Общее решение неоднородного линейного дифференциального уравнения (5.1.18) с постоянными коэффициентами имеет вид: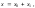(5.1.19)где– общее решение соответствующего однородного уравнения (см. (5.1.10)),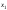– частное решение уравнения (5.1.18).

Особый интерес представляет случай, когда вынуждающая сила – простая периодическая функция времени с частотой :

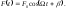(5.1.20)Тогда частотный интеграл (5.1.18) ищем в виде: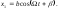(5.1.21)Подстановка в (5.1.18) дает: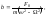(5.1.22) и (5.1.9) можно переписать в виде: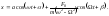(5.1.23)

Произвольные постоянные иопределяются из начальных условий.

Итак, под действием периодической вынуждающей силы система совершает движение, представляющее совокупность двух колебаний – с собственной частотой системы и с частотой вынуждающей силы.

Решение (5.1.23) неприемлемо при (так называемыйрезонанс – 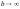). Это вполне естественно, т. к. при больших значенияхколебания перестают быть малыми, и вся изложенная выше теория перестает быть применимой.

Рассмотрим малые колебания вблизи резонанса, т.е. при 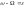, где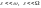. Тогда

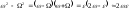. (5.1.24)

В простейшем случае полагаем в (5.1.23) . Тогда

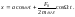(5.1.25)

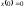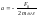Если , тои

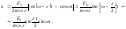(5.1.26)

Поскольку , то функцию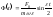(5.1.27)

можно считать медленно изменяющейся по синусоидальному закону амплитудой колебаний системы с собственной частотой . Это так называемыебиения, полученные при сложении колебаний с близкими частотами. Нечто подобное, хотя математически и более сложное, получается при и.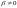

При резонансе вид функции 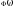изменяется:

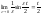(5.1.28) и 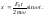(5.1.29)

Амплитуда таких колебаний линейно расчет со временем, и при отклонения могут быть сколь угодно большими – система разрушается.