13 Связь законов сохранения со свойствами симметрии

пространства и времени. Теорема Нётер

Существует определенная связь между законами сохранения энергии, импульса и момента импульса и симметриями пространства-времени: однородностью и изотропностью. В механике эта связь наиболее полно может быть выяснена с помощью уравнений Лагранжа.

Смысл однородности времени в том, что все процессы в замкнутой системе, поставленной в разные моменты времени в одинаковые условия, протекают одинаково. Это означает, что функция Лагранжа явно от времени не зависит, т.е.

(3.3.1) но тогда и(3.3.2)

т. е. обобщенная энергия системы сохраняется. Для потенциальных сил обобщенная энергия совпадает с полной механической энергией. Таким образом, закон сохранения механической энергии замкнутой и свободной от связей системы – следствие уравнений Лагранжа и однородности времени.

Смысл однородности пространства в том, что при сдвиге (перемещении) замкнутой системы в пространстве как единого целого, с сохранением всех остальных условий движения ее тел, все процессы в системе будут протекать одинаково. Для свободной от связей системы в качестве обобщенных координат можно взять декартовы координаты ее частиц. Тогда при элементарном сдвиге (трансляции)

(3.3.3)

все частицы испытывают одинаковый сдвиг (координаты каждой частицы изменяются на ). Варьируя лагранжиан, запишем:

(3.3.4)

В силу однородности пространства параллельный перенос не приводит к изменениям в замкнутой системе, т. е. . Тогда, в силу произвольности, имеем:

(3.3.5)

или(3.3.6)

(3.3.7)

(3.3.8)

т. е. обобщенные импульсы сохраняются. Для потенциальных сил обобщенные импульсы в декартовых координатах для свободной от связей системы совпадают с обычными импульсами . Таким образом, закон сохранения импульса для замкнутой системы – следствие уравнений Лагранжа и однородности пространства.

Смысл изотропности пространства в том, что при повороте замкнутой системы в пространстве как единого целого, с сохранением всех прочих условий, все процессы в системе будут протекать одинаково. Произведем поворот замкнутой свободной от связей системы частиц на бесконечно малый угол вокруг некоторой оси. Смещение частицы при этом, изменение ее скорости, т.е. координаты и скорости преобразуются:

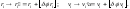(3.3.9)

Найдем изменение лагранжиана, обусловленное поворотом:

(3.3.10)

В силу изотропности пространства , т. е.

(3.3.11)

Производя циклическую перестановку сомножителей в смешанных произведениях, получаем:

(3.3.12)

Учитывая, что

(3.3.13)

(3.3.14)

имеем:

(3.3.15)

произвольно, поэтому

(3.3.16)

Отсюда (3.3.17)

т. е. закон сохранения момента импульса замкнутой системы следует из уравнений Лагранжа и изотропности пространства.

Рассмотренные выше преобразования координат (сдвиг и поворот) и времени непрерывны и обратимы. Описывающая механическую систему функция действия при этом инвариантна. Общую связь между такими преобразованиями и законами сохранения устанавливает теорема Нётер.

В наиболее простом случае теорема Нётер сводится к утверждению о том, что любому непрерывному обратимому преобразованию координат, при котором функция действия данной системы остается инвариантной, соответствует первый интеграл уравнений Лагранжа этой системы.

В самом деле, инвариантность действия означает, что . Отсюда следуют уравнения Лагранжа (см. подраздел 2.5), а также. Если, например, преобразование обобщенных координат сводится к их бесконечно малому изменению при неизменных скоростях, то можно записать:

(3.3.18)

(3.3.19)

и при в силу уравнений Лагранжа условиеозначает, что(3.3.20)