1. Кинематические характеристики частицы

Движение материальной точки (частицы) – изменение ее положения в пространстве относительно других тел с течением времени (перемещение в некоторой системе отсчета).

Система отсчета – совокупность тела (тел) отсчета, системы координат и инструментов для определения расстояний, углов, моментов и промежутков времени.

В теоретических рассуждениях часто используют не реальную систему отсчета, а лишь систему координат, которая в этом случае служит математической моделью системы отсчета.

В любой ортогональной системе координат (декартовой, сферической, цилиндрической и т. п.) определение всех возможных положений точек в пространстве приводит к множеству троек вещественных чисел, обозначающих множество геометрических точек. Это множество составляет геометрическое пространство, которое трехмерно, непрерывно и односвязно. В так называемых инерциальных системах отсчета пространство однородно, изотропно и евклидово. Перечисленные свойства геометрического пространства в классической механике постулируются.

Элементарное механическое событие – попадание частицы в точку с данными координатами в данный момент времени. Оно наблюдается во всех системах отсчета (в этом смысле инвариантно по отношению к системам отсчета), но его координаты в разных системах отсчета могут быть различными.

Механическое движение – непрерывная совокупность последовательных механических событий. Эта совокупность имеет смысл при синхронизации часов в данной системе отсчета. Синхронизация сводится к установке всех часов системы на нуль по сигналу, испускаемому из начала отсчета в нулевой момент времени (по часам, находящимся в начале отсчета). В классической механике полагается, что скорость распространения синхронизирующего сигнала бесконечно велика (много больше скорости движения любых тел).

С помощью синхронизации устанавливается единое время в системе отсчета. Множество моментов времени считается одномерным, непрерывным и однородным. Опыт показывает, что время однонаправлено, т. е. при любом выборе начала отсчета часы дают монотонно увеличивающиеся показания. Перечисленные свойство времени и возможность синхронизации часов мгновенно распространяющимися сигналами в классической механике постулируются.

Если положение частицы в данной системе отсчета определено в каждый момент времени, то ее движение задано (описано). Это задание имеет вид кинематических уравнений движения:

; (1.2.1)

, ,; (1.2.2)

. (1.2.3)

Эти уравнения соответствуют векторному, координатному и естественному способам кинематического описания движения частицы. Здесь –радиус-вектор частицы; x, y, z – ее декартовы координаты; s – путь (своего рода «естественная координата», отсчет которой производится вдоль траектории – годографа радиус-вектора).

Известно, что;(1.2.4)

; ;; (1.2.5)

, ,– углы, образованные радиус-вектором с координатными осями.

Для произвольных (криволинейных) координат q₁, q₂, q₃, связанных с декартовыми координатами преобразованиями

, ,, (1.2.6)

кинематические уравнения движения частицы имеют вид:

, ,. (1.2.7)

Естественный способ задания движения частицы физически (в смысле фиксации ее положения в пространстве) эквивалентен координатному. Уравнение траектории в параметрической форме (параметр – время t) дается выражениями (1.2.2) или (1.2.7). Закон движения частицы по траектории может быть задан аналитически (1.2.3), графически или в виде таблицы.

Скорость – физическая величина, характеризующая быстроту изменения радиус-вектора частицы с течением времени:

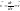. (1.2.8)

Из определения следует, что скорость направлена по касательной к траектории в сторону движения частицы.

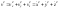; ; (1.2.9)

; ;. (1.2.10)

Физически разложение вектора скорости по трем некомпланарным ортам означает замену одного элементарного перемещения совокупностью трех элементарных перемещений,,, совершаемых независимо друг от друга в любой последовательности (проявлениепринципа независимости движений).

При естественном способе описания движения алгебраическая величина скорости

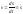. (1.2.11)

В произвольной системе координат с ортами ,,скорость выражается следующим образом (см. подробнее [4, с. 37–38]):

, (1.2.12)

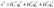, (1.2.13)

где координаты q₁, q₂, q₃ связаны с декартовыми координатами соотношениями (1.2.6), а ,,–коэффициенты Ламэ:

, ,

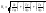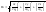. (1.2.14)

В частности, в полярной системе координат .

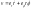
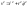Ускорение – физическая величина, характеризующая быстроту изменения скорости частицы с течением времени:

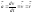, (1.2.15)

. (1.2.16)

В полярной системе координат (см. подробнее [4, с. 40–41])

. (1.2.17)

При естественном способе описания движения ускорение

, (1.2.18)

где – тангенциальное ускорение,– нормальное ускорение;

2 Преобразования кинематических характеристик частицы при

относительном движении систем отсчета

Рассмотрим следующую задачу, имеющую важные приложения в механике: зная кинематические характеристики частицы в некоторой системе отсчета, найти соответствующие характеристики в другой системе отсчета, относительно которой первая система движется известным образом. Решим данную задачу для общего случая движения системы отсчета и частицы в ней.

Назовем условно систему отсчета 0₁XYZ, относительно которой надо определить характеристики движения т. М (рисунок 1.4.1), неподвижной, а движение т. М относительно нее абсолютным; систему отсчета 0xyz подвижной, а движение т. М относительно нее относительным (характеристики этого движения считаем в данной задаче известными); движение покоящейся в системе 0xyz точки относительно системы 0₁XYZ назовем переносным. Переносное движение включает перемещение начала 0 относительно начала 0₁ и поворот осей СК 0xyz в пространстве относительно осей СК 0₁XYZ; характеристики переносного движения также считаем известными.

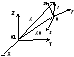
Рисунок 1.4.1

Из рисунка 1.4.1 видно, что для радиус-векторов выполняется соотношение:

. (1.4.1)

Физически это равенство далеко не тривиально, т. к. величины измеряются вразных системах отсчета. Равенство основано на допущении о том, что длина и направление отрезка не зависят от скорости и характера его движения в данной системе отсчета. Это вытекает из постулата о бесконечно быстрых сигналах и возможной синхронизации с их помощью часов в движущихся системах. Все дальнейшие рассуждения основаны на допущении, что момент времени, в который происходит какое-либо событие, одинаков во всех системах отсчета, а значит и одинаковы промежутки времени между двумя событиями в разных системах отсчета:

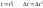. (1.4.2)

Тогда длина данного отрезка (расстояние между одновременно определенными положениями его концов) во всех системах отсчета одинакова. В рассматриваемой нами задаче – модуль (длина) векторакак в подвижной, так и в неподвижной системах отсчета; равенство (1.4.1) можно рассматривать в проекциях на оси обеих систем координат. В силу этого равенство (1.4.1) служит основанием для всех кинематических соотношений сложного движения частицы в нерелятивистской классической механике.

Разложим в (1.4.1) радиус-вектор по ортам подвижной СК и продифференцируем (1.4.1) по времени:

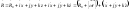(1.4.3)

где – угловая скорость вращения СК 0xyz. Здесь учтено, что 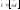,,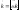. Таким образом,

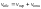, (1.4.4)

т. е. скорость абсолютного движения складывается из скоростей переносного и относительного движений. Первое слагаемое переносной скорости представляет собой скорость поступательного движения частицы вместе с СК 0xyz относительно СК 0₁XYZ (скорость начала 0 относительно начала 0₁), второе слагаемое – скорость частицы, обусловленная вращением СК 0xyz относительно СК 0₁XYZ.

Для нахождения ускорений продифференцируем (1.4.3) по времени:

. (1.4.5)

Здесь ускорение абсолютного движения частицы (относительно СК 0₁XYZ). Относительное ускорение получаем, полагая постоянными величинами:

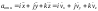. (1.4.6)

Для выделения переносного ускорения полагаем относительные координаты x, y, z постоянными. Это дает (см. подробнее в [4, с. 59]):

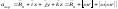(1.4.7)

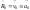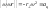Здесь –переносное поступательное ускорение (ускорение начала 0 относительно начала 0₁); –переносное вращательное (тангенциальное) ускорение (обусловлено неравномерностью вращения СК 0xyz относительно СК 0₁XYZ); –переносное центростремительное ускорение (см. подробнее в [4, с. 59]). Таким образом,

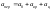. (1.4.8)

В правой части (1.4.5) остались слагаемые, не отнесенные к относительному или переносному ускорениям. Это ускорение Кориолиса

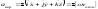. (1.4.9)

Легко видеть, что ускорение Кориолиса имеет место только при движении частицы под углом к оси вращения во вращающейся системе координат.

Теорема Кориолиса: абсолютное ускорение определяется геометрической суммой переносного, относительного и кориолисова ускорений, т. е.

. (1.4.10)

Если подвижная СК движется относительно неподвижной равномерно, прямолинейно и поступательно ср скоростью , то

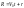, . (1.4.11)

В силу изотропности пространства без ограничения общности можно выбрать направления осей 0₁Х и 0х совпадающими со скоростью 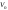движения точки 0 в системе 0₁XYZ, а за начальный момент времени принять момент совпадения точек 0 и 0₁. Тогда в координатном представлении имеем:

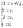
(1.4.12)

Это формулы преобразований Галилея для координат и скоростей. Ускорение инвариантно относительно преобразований Галилея:

. (1.4.13)