
Chainov_Ivashenko_Konstr_dvs_1 / Чайнов Иващенко - Конструирование ДВС
.pdf
саны исходные дифференциальные уравнения и функционалы, к есте ственным координатам.
При преобразовании коорди нат можно использовать комби нации функций формы Ni, кото рые используются для аппрокси мации искомой функции в преде лах конечного элемента. В этом случае конечный элемент называ ется изопараметрическим. В ка честве узловых параметров при преобразовании координат ис пользуются декартовы координа ты узловых точек. Например, в случае одномерного квадратично го элемента (рис. 2.10, а):
x N1 x1 N 2 x2 N 3 x3 . (2.78)
Для вычисления производной функций формы Ni, которые теперь записаны в естественных коорди натах, используются соотношения
|
dN i |
|
[J] |
dN i |
, |
(2.79) |
||||||
|
|
d2 |
|
dx |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
где [J] |
dN1 |
|
x1 |
|
dN 2 |
|
x2 |
|
dN 3 |
x3 |
||
d2 |
|
d2 |
|
d2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|||
называется матрицей преобразова ния Якоби. Элемент длины dx = = det[J]d2.
Искомая производная:
|
|
|
dN i |
|
[J] 1 |
dN i |
. |
(2.80) |
||||
|
|
|
|
dx |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
d2 |
|
||
В двухмерном случае имеем |
||||||||||||
N i |
|
|
N i |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
x |
(2.81) |
|||||
|
|
|
|
|
# |
[J] |
# , |
|||||
|
N i |
|
|
N i |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
9 |
|
y |
|
||||||||
|
|
|
|
|
|
|||||||
x |
x |
|
|
|
|
|||||||
|
|
|
|
! |
|
|
|
|
||||
2 |
2 |
|
|
|
|
|||||||
где [J] |
|
|
|
y |
! . |
|
|
|
|
|||
x |
! |
|
|
|
|
|||||||
9 |
9! |
|
|
|
|
|||||||
Элементарная площадь dF = = dxdy = det[J]d2d9.
Вектор искомых производных
N i |
|
|
|
|
N i |
|
|
|||||||
|
x |
|
|
|
|
|
2 |
|
|
|
||||
|
|
|
1 |
|
|
|
|
(2.82) |
||||||
|
|
# [J] |
|
|
|
|
|
# . |
||||||
|
N i |
|
|
|
|
|
N i |
|
|
|||||
|
|
|
|
|
|
|||||||||
y |
|
|
|
|
|
9 |
|
|
||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В трехмерном случае имеем |
||||||||||||||
|
N i |
|
|
|
|
N i |
|
|
|
|||||
|
2 |
|
|
|
|
|
x |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
N |
i |
|
|
|
|
N |
i |
|
|
|
|||
|
|
|
# [J] |
|
|
# , |
(2.83) |
|||||||
9 |
|
y |
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
N i |
|
|
|
|
N i |
|
|
|
|||||
|
: |
|
|
|
|
|
z |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
x |
y |
z |
|
|
|
|
|
|
||||||
2 |
|
|
! |
|
|
|
|
|
||||||
2 |
2 |
|
|
|
|
|
||||||||
|
|
y |
z |
! |
|
|
|
|
|
|||||
где [J] x |
! . |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||
9 |
9 |
9! |
|
|
|
|
|
|||||||
x |
y |
z |
! |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
! |
|
|
|
|
|
||
: |
|
: |
: |
|
|
|
|
|
|
|
||||
Элементарный |
|
|
объем |
dV = |
||||||||||
= dxdydz = det[J]d2d9d:. |
|
|
|
|||||||||||
Вектор искомых производных
|
N i |
|
|
|
|
N i |
|
|
||
|
x |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
N |
i |
|
|
1 |
|
N |
i |
|
(2.84) |
|
|
# |
[J] |
|
|
# . |
||||
|
y |
|
|
|
|
|
9 |
|
|
|
|
N i |
|
|
|
|
N i |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
: |
|
|||||
|
|
|
|
|
|
|
|
|||
Приведенные соотношения ис пользуются при вычислении харак теристик конечных элементов при решении различных задач с помо щью МКЭ.
51

2.4.1. Расчет теплового состояния деталей двигателя
При решении задачи стационар ной теплопроводности с помощью МКЭ неизвестными являются тем пературы в узлах конечно элемент ной сетки, покрывающей область, занимаемую рассчитываемой дета лью. Температуру в узлах определя ют с помощью минимизации соот ветствующего функционала по ис комым температурам узлов.
Выражения функционалов для плоской и осесимметричной задач при постоянных теплофизических характеристиках материала получа ются из формулы (2.9) и соответст венно имеют вид
|
|
|
|
|
|
T |
2 |
|
Ф(T ) |
|
|
|
|
||||
|
2 |
|
|
|
||||
|
||||||||
|
|
|
|
x |
|
|||
|
|
V |
|
|
|
|
|
|
|
T |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
! QT #dV |
|||||
|
|
|
! |
|
|
|
|
|
|
y |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
tq0TdS t (T Tcp )2 dS ; (2.85) |
||||||||
S2 |
|
|
|
|
S3 |
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
T |
2 |
Ф(T ) |
|
|
|
|
||||
|
2 |
|
|
|||||
|
|
|
|
|
r |
|
||
|
|
|
V |
|
|
|
|
|
T |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
! QT #dV |
||||
|
|
|||||||
z |
|
|
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 rq0TdS r (T Tcp )2 dS . |
||||||||
S2 |
|
|
|
|
|
S3 |
|
|
|
|
|
|
|
|
|
|
(2.86) |
Для плоской задачи элементар ный объем dV = tdF, где dF = dxdy, а для осесимметричной dV = 2 rdF, где dF = drdz.
Минимизация функционалов должна производиться на выбран ном множестве узловых значений температур [Т1, …, Тn], где число уз
лов n достаточно велико. Так как функции Ni определяются на от дельных элементах, а аппроксими рующие полиномы должны удовле творять условиям полноты и согла сованности на границах соседних элементов, то общий функционал, относящийся ко всей области, за нимаемой телом, заменяется сум мой функционалов отдельных эле ментов в соответствии с формулой (2.56, а).
Математически минимизация функционала Ф(Т) выражается сле дующим образом:
m |
e |
(T ) 0. (2.87) |
Ф(T ) 6 Ф |
|
|
{T } e 1 {T } |
||
Дифференцируя в соответствии |
||
с (2.9) выражение |
|
функционала |
Фе(Т) одного элемента с объемом
V e по температуре Ti |
i го узла, по |
|||||||||||||||||||
лучаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Фe (T ) |
|
|
|
|
T |
|
T |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Ti |
|
x Ti |
|
|
|
||||||||||||||
|
|
V |
e |
|
x |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
T |
|
|
T |
|
|
T |
|
|
T |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
! |
|
|
|
y Ti |
|
|
|
z Ti z |
|
||||||||||||||
|
|
T |
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
||||
Q |
|
|
#dV q0 |
|
|
|
dF |
|
|
|||||||||||
Ti |
Ti |
|
|
|||||||||||||||||
|
|
|
|
|
F e |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
(T Tcp ) |
T |
dF . |
|
|
|
|
|
(2.88) |
||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
F e |
|
|
|
|
|
|
Ti |
|
|
|
|
|
|
|
|
|
|
||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При этом два последних инте |
|||||||||||||||||||
грала по площади появляются толь ко у элементов на границе области, занимаемой телом, где заданы гра ничные условия теплообмена 2 го или 3 го рода. При вычислении производных в выражении (2.88) и ему подобных следует иметь в виду,
что |
T |
|
N1 |
, |
N 2 |
,... {T }e |
. Здесь |
||
|
|
|
|
|
|||||
|
|
|
|
||||||
|
x |
x |
|
x |
! |
|
|||
|
|
|
|
|
|||||
52
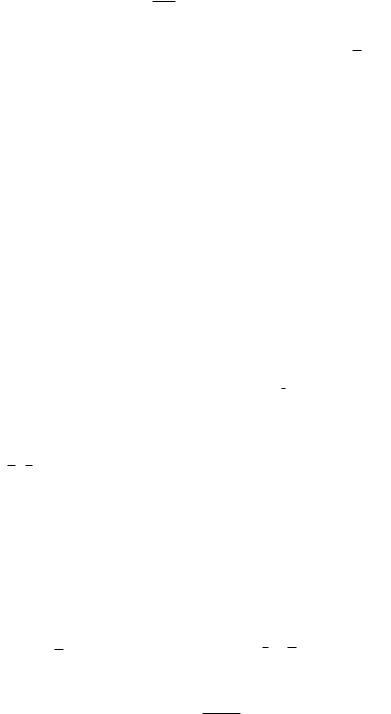
{T}e – вектор узловых температур элемента. Аналогично определяют
T T T
ся y и z . Кроме того, Ti
В результате для одного элемента с учетом всех его узловых точек в со ответствии с (2.88) получим
Фe (T ) |
(2.89) |
[He ]{T e } { f e }, |
|
{T e } |
|
где [He] – матрица теплопроводно сти элемента; {f e} – вектор тепло вой нагрузки элемента.
Используя правило перемно жения матриц и соотношения (2.73), (2.74), вычисляют инте гралы в выражениях матрицы те плопроводности и вектора теп ловой нагрузки элемента. В слу чае треугольных и тетраэдальных элементов интегрирование осу ществляют с помощью L коор динат. Для выражений, содержа щих параметры теплообмена , q0, интегрирование проводят только по граням элементов, рас положенных на границе тела, по которой осуществляется теплооб мен. Параметры , q0 часто заме няются в пределах границ эле мента осредненными значения
ми 4 q0 .
В случае симплексного тре угольного элемента (рис. 2.9, б), принимая за наружную грань 1 3 длиной l, вдоль которой осущест вляется интегрирование и N2 = = L2 = 0, получим для плоской задачи:
[H |
e |
] |
|
t |
[he ]T [he ] |
|
||||
|
|
|
|
|
||||||
|
|
|
4 |
|
||||||
|
|
tl |
1 |
0 |
0,5 |
|
|
|||
|
|
|
0 |
0 |
! |
; |
(2.90) |
|||
|
|
3 |
0 |
! |
||||||
|
|
|
0,5 |
0 |
1 |
! |
|
|
||
|
|
|
|
|
|
|||||
|
|
b |
b |
b |
|
|
||||
[he ] 1 |
2 |
3 |
! , |
|
||||||
|
|
c1 |
c2 |
c3 |
|
|
||||
|
|
|
|
Qt |
|
|
||||
{ f e } |
|
|
|
; |
|
|
||||
3 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
t(q |
0 |
Tcp )l |
||||||
; 1# |
|
|
|
|
|
|
|
|
0# . (2.91) |
|
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
1 |
|
Из формулы (2.91) следует, что при наличии в элементе теплового источника генерируемая теплота распределяется поровну между уз лами элемента. Из выражения мат рицы [he], называемой матрицей градиентов, видно, что в случае плоской задачи градиент темпера туры в пределах линейного тре угольного элемента не меняется. Это обусловливает необходимость более мелкой разбивки детали на конечные элементы в тех местах, где ожидается значительное изме нение градиента температуры.
Для осесимметричной задачи:
[He ] |
r |
|
[he ]T [he ] |
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
||||||||
|
l |
3r |
|
r |
|
0 |
|
r |
r |
|
|
|
|
|
|
1 |
0 |
3 |
0 |
|
1 |
0 |
3 |
! |
; |
(2.92) |
|||
6 |
|
|
|
|
|
! |
||||||||
|
r1 |
r3 |
0 |
|
r1 3r3 ! |
|
|
|||||||
|
|
|
|
|
||||||||||
[he ] |
b |
|
b |
|
b |
|
; |
|
|
|
|
|
||
1 |
|
2 |
3 |
! |
|
|
|
|
|
|||||
|
|
c1 |
|
c2 |
c3 |
|
|
|
|
|
|
|
||
|
2r |
|
r |
|
r |
|
|
|
||
|
Q |
1 |
|
|
2 |
|
3 |
|
|
|
{ f e } |
r1 |
|
2r2 r3 # |
|||||||
|
6 r |
|
r |
2 |
2r |
3 |
|
|
||
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2r r |
|
|
|
|
|
l(q |
0 |
|
|
T |
cp |
) |
1 |
3 |
|
(2.93) |
|
|
|
|
|
|
|
0 |
|
# . |
||||
|
|
3 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
r 2r |
3 |
|
|
||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
53

В случае трехмерной задачи для тетраэдального элемента (рис. 2.9, в), принимая за наруж ную грань 1 2 4, по которой про исходит теплообмен и где N3 = = L3 = 0, получим
[He ] [he ]T [he ]
|
|
|
|
36V |
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
0,5 |
0 |
0,5 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! |
|
0,5 |
|
1 |
0 |
0,5! |
; (2.94) |
||||||||||
|
6 |
0 |
|
0 |
0 |
0 ! |
|
||||||||
|
|
|
|
|
|
|
0,5 |
0 |
1 |
! |
|
||||
|
|
|
0,5 |
|
|
||||||||||
|
|
|
b1 |
b2 |
b3 |
b4 |
|
|
|||||||
[he ] c |
c |
2 |
c |
3 |
c |
4 |
! |
; |
|||||||
|
|
|
|
1 |
|
|
|
|
|
! |
|
||||
|
|
|
d1 |
d2 |
d3 |
d4 ! |
|
||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{ f e } |
QV 1 |
|
|
|
|
|
|
||||||||
|
|
|
|
# |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
4 |
|
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(q |
|
|
|
|
|
|
|
|
|
|
|
|||
|
0 |
T ) 1 |
|
|
|
|
|
||||||||
|
|
|
|
|
cp |
|
|
# . |
|
|
|
(2.95) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
3 |
|
|
|
|
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
Формулы (2.90)–(2.95) могут быть уточнены при замене осред ненных наружных значений , q0 и Тср на наружных гранях элементов, где происходит теплообмен, напри мер, линейными соотношениями типа
q0 Tcp |
|
|
|
|
|
|
q01 |
( Tcp )1 |
|
||||
|
|
( T |
|
) |
|
|
q |
02 |
cp |
2 |
|
||
[L1 L2 0 L4 ] |
0 |
|
# . |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q04 |
( Tcp )4 |
|||||
|
|
|
|
(2.96) |
||
При этом вектор тепловой на грузки {f e} примет вид
|
|
|
|
|
1 |
|
|
|
2 |
1 |
0 |
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
1 |
! |
|
|
|
|
|
QV 1 |
|
|
1 |
! |
|
||||||||
{ f e } |
|
|
|
# |
|
|
|
|
|
|
|
; |
||||
4 |
|
12 |
|
0 |
|
|||||||||||
|
|
|
|
1 |
|
0 0 |
0! |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
2 |
! |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|||||
q01 ( Tср )1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
( T |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
q |
02 |
ср |
2 |
|
|
|
|
|
|
(2.97) |
||||||
; |
|
0 |
|
#. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( Tср )4 |
|
|
|
|
|
|
|
|
|
|||||
q04 |
|
|
|
|
|
|
|
|
|
|||||||
Подставив в уравнение (2.87) выражение (2.89), получают систе му линейных алгебраических урав нений относительно n неизвестных узловых температур. В матричной форме система имеет вид
|
[H]{T } { f }, |
(2.98) |
m |
m |
|
где [H] 6[He ]; { f } 6[ f e ]. |
|
|
e 1 |
e 1 |
|
Рассмотрим нестационарную задачу теплопроводности, имею щую важное значение при оценке теплового состояния деталей в ус ловиях неустановившихся режимов работы двигателя. При быстром из менении скоростного и нагрузоч ного режимов работы возможны случаи, когда уровень тепловых на грузок оказывается более высоким, чем при работе на номинальном режиме. Существенные изменения режима работы двигателя приводят к макротеплосменам, т.е. к значи тельным изменениям теплового со стояния всего объема деталей во времени.
Изменение теплового состояния деталей связано также и с цикличе ским характером протекания рабо чего процесса двигателя, вызываю щим так называемые микротепло
54

смены, которые распространяются на сравнительно небольшой объем металла поверхностных слоев сте нок камеры сгорания. Амплитуды колебаний температуры этих слоев незначительны и уменьшаются с повышением скоростного режима работы двигателя, а также расстоя ния от поверхности. В случае ис пользования в качестве материалов элементов ЦПГ керамики, компо зитов и других материалов с низ кой теплопроводностью амплитуды колебаний температуры поверхно сти могут достигать 100–150 С и выше.
Решение задачи о нестационар ном температурном поле связано с рассмотрением дифференциально го уравнения теплопроводности (2.1) (в общем случае) или уравне ния (2.2) (при постоянных тепло физических характеристиках мате риала).
Аналитические решения неста ционарной задачи возможны лишь для простейших одномерных слу чаев. Поэтому применительно к деталям ЦПГ двигателя использу ются численные методы, в частно сти МКЭ. Искомая температура Т(x, y, z, ) представляется как
T (x, y, z, ) [N]{T e ( )}. (2.99)
Наряду с примененной выше, в случае стационарной задачи, ва риационной формулировкой ши роко используется более универ сальный невариационный подход. Весьма распространенным здесь является известный метод Бубно ва–Галеркина, являющийся част ным случаем метода невязок. При ближенное решение уравнения (2.2) нестационарной теплопровод ности получается на базе рассмот
рения соответствующего интеграла взвешенной невязки по области V, занимаемой телом
W pRdV 0, |
(2.100) |
V |
|
где R – невязка или погрешность, возникающая при подстановке приближенного решения T в урав нение (2.2); р = 1, 2, …, n – число узловых параметров; Wр – опреде ляемые последовательно по облас ти V интерполянты.
При применении МКЭ в качест ве Wр выбираются функции формы Nр и уравнение (2.100) принимает вид
N pRdV 0. |
(2.101) |
V |
|
Подставляя выражение (2.100) в уравнение (2.2) с последующим оп ределением невязки R и используя интегральную формулировку выра жения (2.101), приходят к системе обыкновенных дифференциальных уравнений первого порядка отно сительно узловых значений темпе ратур Tp( ), которая в матричной форме имеет вид
|
[c] |
{T } |
[H]{T } { f }, (2.102) |
|
|
||
|
|
|
|
где [c] |
– матрица теплоемкости, |
||
m |
|
|
|
[c] 6[c e ];[c e ] c [N]T [N]dV . |
|||
e 1 |
|
|
V e |
Иногда по аналогии с задачами динамики матрицу [c] называют матрицей демпфирования.
С помощью L координат инте грал в выражении [ce] определяет ся по формулам (2.73) и (2.74). Для плоской и осесимметричной задач
55

|
|
|
t |
2 |
1 |
1 |
|
|||
[c e ] |
c |
1 2 1 |
!; |
|||||||
|
|
|
||||||||
|
|
12 |
|
1 |
2 |
! |
|
|||
|
|
|
|
|
1 |
! |
(2.103) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
1 |
|
[c e ] |
r c 1 2 1 |
!. |
||||||||
|
|
6 |
|
|
|
|
|
! |
||
|
|
|
1 |
|
1 |
2! |
||||
|
|
|
|
|
|
|
||||
Наиболее простым приближен ным способом решения системы дифференциальных уравнений яв ляется переход от производной температуры по времени к ее ко нечно разностному выражению
T |
|
(T1 T0 ) |
, (2.104) |
|
|
|
|||
|
|
где Т0 и Т1 – соответственно на чальные и конечные значения тем пературы в пределах временного интервала .
При применении центральной разностной схемы величины {T } и { f } определяются как среднее зна чение для интервала , т.е.
|
|
|
{T } |
|
{T } |
|
|
|
{T } |
0 |
|||||||
|
1 |
|
; |
|||||
|
|
2 |
|
|||||
|
|
|
|
|
# (2.105) |
|||
|
|
|
{ f }0 { f }1 |
|||||
{ f } |
|
|
||||||
|
|
|
. |
|||||
|
|
2 |
||||||
|
|
|
|
|
|
|
||
С учетом выражения (2.105) сис тема уравнений (2.102) принимает вид
|
|
2 |
|
|
|
|
|
[H] |
|
[c]#{T1 |
} |
|
|
||
|
|
|
|||||
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
[c] [H] {T }0 |
2{ f }. |
(2.106) |
|||
|
|||||||
|
|
|
|
|
|
||
Рассмотренная расчетная схема является явной по времени. Значе ния узловых температур {T}0 в мо мент времени считаются извест ными и из системы уравнений
(2.106) находят узловые температу ры в момент времени ( + ). Дан ное решение предполагает посто
T
янство производной в течение
интервала . Существуют и другие более совершенные способы реше ния. Так, если предположить, что в пределах вектор {T } температур интерполируется по некоторым его значениям, в частности, линейно по двум значениям {T }0 и {T }1, со ответствующим началу и концу ин тервала , то
|
T [N |
0 |
N |
1 |
] {T |
}0 , (2.107) |
|||
|
|
|
|
|
|
# |
|||
|
|
|
|
|
|
{T |
}1 |
||
где N 0 |
|
( ) |
; N1 |
|
|
|
; 0 < < . |
||
|
|
|
|||||||
|
|
|
|
|
|
|
|||
Такая постановка задачи преду сматривает распространение мето да конечных элементов и для коор динаты времени. В этом случае
T |
|
1 |
{T }0 |
|
|
|
|
|
[ 1 |
1] |
#. (2.108) |
|
|
||||
|
|
|
{T }1 |
|
|
Подставив зависимости (2.107) и (2.108) в выражение (2.102) и ум ножив его на N1, после интегриро вания в пределах получим систе му алгебраических уравнений от носительно неизвестных значений вектора температур {Т}1, значения вектора температур {Т}0 в начале интервала при этом известны
{T }1 {2 3[H] [c]
3[H] [c]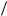 } 1 ;
} 1 ;
; [[H]1 3 [c]
3 [c] ]{T }0
]{T }0
|
2 |
|
|
|
[2 ( ) |
|
|
(2.109) |
|
|
] { f } d #. |
|||
|
|
0 |
|
|
|
|
|
|
|
56

2.4.2. Расчет напряженно деформированного состояния деталей двигателя
При расчете теплонапряженных деталей данному этапу предшеству ет определение теплового состоя ния, поэтому все, связанное с раз бивкой детали на элементы и их описанием, берется в этом случае в готовом виде. Если температура де тали заведомо близка к постоянной по объему (например, шатуны, подвеска коленчатого вала и др.), то тепловое состояние не рассчи тывается, но требуется выполнить все операции, связанные с разбив кой детали на элементы и их опи санием.
При решении задачи в переме щениях вектор перемещений точек в пределах элемента , выражается через компоненты перемещений уз лов {,e} элементов соотношениями (2.60–2.62). Компоненты переме щений n узлов являются неизвест ными задачи. Их определяют мини мизацией функционала (2.28), вы ражающего полную потенциальную энергию системы. При этом ис пользуется зависимость (2.87), в ко торой величины Ф и {T } следует за менить соответственно на П и {,}.
Для минимизации функционала П необходимо вычислить частные производные от функционалов Пе отдельных элементов по перемеще ниям узлов, затем просуммировать одноименные производные, т.е. производные для различных эле ментов, но по перемещениям одно го узла, и результат приравнять нулю.
Как и при решении задачи тепло проводности вклад в общую сумму дадут лишь элементы, включающие узел, по перемещению которого вы числяются частные производные.
В результате получают систему линейных алгебраических уравне ний относительно компонентов пе ремещений узлов. Для двухмерных задач порядок системы равен 2n, так как перемещение ,i каждого уз ла характеризуется двумя компо нентами ui и vi, а для трехмерных задач порядок системы равен 3n, так как {, i }T [ui vi wi ].
Для плоской и осесимметрич ной задач напряженно деформиро ванное состояние в точке характе ризуется соответственно следую щими компонентами
{ }T [ x y |
xy ]; |
||
{+}T [+ x |
+ y xy ]; |
||
{,}T [u |
v] |
|
|
и |
|
|
|
{ }T [ r |
z |
) |
r z ]; |
{+}T [+ r |
+ z |
+ ) |
r z ]; |
{,}T [u v].
Оставшиеся компоненты объем ного напряженно деформирован ного состояния в данном случае равны нулю. Так, для плоского на пряженно деформированного со
стояния z = yz = zx = 0; yz = zx = 0. Так как задача решается в пере мещениях, с помощью формул (2.21) компоненты деформации элемента {+e} выражают через ком поненты перемещения, используя
57

для последних интерполяционную зависимость (2.60)
{+ e } [B]{, e }, |
(2.110) |
где [В] – матрица деформации, получаемая дифференцированием матрицы [N] с учетом зависимо
стей (2.21). Для линейного тре угольного элемента [В] = [В1 В2 В3]; для линейного тетраэдра [В] =
=[В1 В2 В3 В4].
Вслучае плоской и осесиммет
ричной задач
|
|
|
|
|
|
N i |
|
|
|
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
! |
|
|||
|
|
|
|
|
|
|
|
|
|
|
N i |
! |
|
|||||
[Bi ] |
|
|
0 |
|
|
|
|
! |
|
|||||||||
|
|
|
|
|
|
y |
! |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
N i |
|
|
|
|
N i |
! |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
y |
|
|
|
|
x |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
b |
0 |
|
|
|
|
||||||||
|
1 |
|
|
|
i |
|
|
|
! |
|
|
|
(2.111) |
|||||
|
|
|
0 |
ci |
!; |
|
|
|
||||||||||
|
2 |
|
|
|
||||||||||||||
|
|
|
|
|
ci |
bi |
! |
|
|
|
|
|||||||
|
|
|
N i |
|
|
|
0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! |
|
|
||
|
|
|
|
|
r |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
N |
|
! |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
! |
|
|
||||
|
|
|
|
|
|
|
z |
|
|
|
||||||||
[Bi |
] |
|
|
|
|
|
|
|
|
|
|
! |
|
|
||||
|
|
|
N i |
|
|
|
0 |
|
! |
|
|
|||||||
|
|
|
|
|
r |
|
|
|
|
|
! |
|
|
|||||
|
|
|
|
|
|
|
N i |
! |
|
|
||||||||
|
|
|
N i |
|
|
! |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
r |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
bi |
|
|
||
|
|
|
0 |
|
|||
|
1 |
|
|||||
|
|
|
|||||
|
|
a |
b |
|
ci z |
||
2 |
|||||||
|
|
|
|||||
|
|
r |
i |
|
r |
||
|
|
|
ci |
|
|
||
0 |
|
|
|
ci |
! |
|
|
! |
, |
(2.112) |
|
0 |
! |
||
|
! |
|
|
bi |
! |
|
|
где i принимает значения 1, 2, 3. В случае трехмерной задачи
N i |
0 |
|
|
|
0 |
|
|
|||||
|
x |
|
|
|
|
! |
||||||
|
N i |
|
|
|
|
! |
||||||
|
|
|
|
|
|
|
|
|||||
|
0 |
|
|
|
|
0 |
|
! |
||||
|
|
y |
|
|
|
|
||||||
|
|
|
|
|
|
|
N |
|
! |
|||
|
0 |
|
|
0 |
|
|
i |
! |
||||
|
|
|
|
|
|
z |
! |
|||||
[Bi ] |
|
|
|
|
N i |
|
|
|
! |
|||
|
|
|
|
|
|
|
|
|||||
|
N i |
|
|
|
|
! |
||||||
|
|
|
|
|
|
|
|
|
0 |
|
||
y |
x |
|
|
|
|
|||||||
|
|
|
|
|
|
! |
||||||
|
0 |
|
|
N |
i |
|
N |
i |
! |
|||
|
|
|
|
|
|
|
! |
|||||
|
|
z |
|
|
|
y |
|
|||||
|
|
|
|
|
|
|
|
|
! |
|||
N i |
0 |
|
|
N i |
! |
|||||||
z |
|
|
|
x |
|
! |
||||||
|
|
|
|
|
||||||||
|
|
|
|
bi |
0 |
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|
0 |
ci |
|
0 |
! |
|
|
||
|
|
1 |
|
0 |
0 |
|
di |
! |
|
(2.113) |
||
|
|
|
|
|
|
|
|
!, |
|
|||
|
|
|
|
|
|
|
|
|||||
|
6V |
ci |
bi |
|
0 |
! |
|
|
||||
|
|
|
|
0 |
di |
|
ci |
! |
|
|
||
|
|
|
|
|
0 |
|
bi |
! |
|
|
||
|
|
|
|
di |
|
|
|
|
||||
где i принимает значения 1, 2, 3, 4. Температурная деформация, рас
сматриваемая как разновидность на чальной деформации, для плоской, осесимметричной и трехмерной за дач может быть представлена в мат ричной форме соответственно сле
дующим образом: |
|
|
||
{+ 0e }T T T e [1 |
1 |
0]; |
|
|
{+ 0e }T |
T T e [1 |
1 |
1 |
0]; |
{+ 0e }T |
T T e [1 |
1 |
1 |
0 0 0]. |
Для изотропного материала связь напряжений с деформациями выражается зависимостями (2.24). Разрешая последние относительно напряжений, окончательно полу чим
{ e } [D]({+ e } {+ 0e }). |
(2.114) |
Матрица упругости [D] для пло ской, осесимметричной и трехмер ной задач соответственно имеет следующий вид:
58

для плоской задачи |
|
|
полной потенциальной энергии |
|||||||
|
|
|
|
|
|
|
|
|
системы П в матричной форме |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
! |
m |
|
|
[D] |
|
E |
− |
1 |
|
|
0 |
!; (2.115) |
П 6 0,5{, e }T [B]T [D][B]{, e }dV |
|
|
|
|
|
|
||||||
1 |
− 2 |
|
1 |
− |
! |
e 1 V e |
|
|||
|
|
|
0 |
0 |
! |
{, e }T [B]T [D]{+ 0e }dV |
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
V e
для осесимметричной задачи
[D] |
|
E(1 −) |
|
; |
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||
(1 −)(1 2−) |
|
|
|
||||||||||||
|
1 |
|
|
|
− |
− |
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
! |
||||||
1 |
− 1 |
− |
|||||||||||||
|
|
|
|
! |
|||||||||||
− |
|
|
|
|
|
|
− |
|
|
||||||
|
|
|
|
|
|
1 |
|
|
0 |
! |
|||||
|
|
|
|
|
|
|
|
|
|
||||||
; 1 − |
1 |
− |
|
|
!; (2.116) |
||||||||||
|
− |
|
|
|
− |
1 |
0 |
! |
|||||||
|
|
|
|
|
|
|
|
|
! |
||||||
|
− 1 |
− |
|||||||||||||
1 |
|
|
|
(1 2−) |
! |
||||||||||
|
0 |
|
|
|
0 |
|
|
0 |
|
! |
|||||
|
|
|
|
|
|
|
2(1 −) |
! |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
для трехмерной задачи
{, e }T [N]T {P}dV
V e
|
e |
T |
T |
|
|
{, |
|
|
|||
|
} |
[N] |
{p/ }dF |
||
F e |
|
|
|
|
|
{, e }T {R}, |
|
(2.118) |
|||
где {P} – вектор объемных сил; {p/} – вектор поверхностной рас пределенной нагрузки; {R} – век тор сосредоточенной нагрузки.
При описании элемента индекс е сохраняется только при неизвест ных узловых перемещениях, хотя компоненты матрицы деформации [B], векторы объемных сил и по
|
|
|
|
1 |
|
|
− |
|
− |
|
|
0 |
|
|
0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
− |
1 − |
|
|
|
|
||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|||||||
|
|
|
− |
|
|
|
− |
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
|
|
|
0 |
|
|
0 |
||||
|
|
|
1 − |
1 − |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
− |
− |
1 |
|
|
0 |
|
|
0 |
|||||
|
|
E(1 −) |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
− 1 |
− |
|
|
|
|
|||||||||
[D] |
|
1 |
|
|
|
|
2−) |
|
|||||||||
|
|
|
|
|
|
|
|
|
(1 |
|
|||||||
(1 |
−)(1 2−) |
0 |
|
|
0 |
0 |
0 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2(1 |
−) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1 2−) |
||
|
|
|
|
0 |
|
|
0 |
0 |
|
|
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
2(1 −) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
0 |
|
|
0 |
0 |
|
|
0 |
|
|
0 |
|||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
! |
|
|
|
! |
|
0 |
! |
|
! |
|
|
|
|
|
0 |
! |
|
! |
|
|
|
! |
(2.117) |
0 |
!. |
|
! |
|
|
|
|
|
|
! |
|
0 |
! |
|
|
! |
|
(1 2−)! |
|
|
|
! |
|
2(1 −) |
|
|
Подставив в формулу (2.28) соотношения (2.110) и (2.114) и выполнив суммирование по всем элементам, получим выражение
верхностной нагрузки вычисляют ся для каждого элемента. При рас чете теплонапряженных деталей, если требуется учесть зависимость
59

Е, − и Т от температуры, компо ненты вектора температурной де формации {+0} и матрицы упругости [D] также вычисляются для каждо го элемента.
Дифференцирование полной потенциальной энергии по векто ру узловых перемещений произ водится аналогично дифференци рованию функционала Ф(Т ) по вектору {Т } с использованием за висимости (2.88). Минимизация полной потенциальной энергии системы П приводит к соотноше нию
П |
m |
|
|
||
6 |
[B]T [D][B]dV {, e } |
||||
|
|||||
{,} |
e |
|
|
|
|
|
1 |
V e |
|||
[B]T [D]{+ 0 }dV
Ve
[N]T {P}dV
V e |
|
|
|
|
|
|
{R} |
0. |
|
[N]T {p/ }dF |
(2.119) |
|||
V e |
|
|
|
|
|
|
|
|
|
Вектор |
узловых |
перемещений |
||
{,e} при интегрировании по объему элемента в локальной системе ко ординат является постоянным. При этом важное значение имеет интеграл
[k e ] [B]T [D][B]dV , (2.120)
V e
называемый матрицей жесткости элемента.
Остальные интегралы в соотно шении (2.119) составляют вектор нагрузки {G e } элемента, т.е.
{G e } [B]T [D]{+ 0 }dV
Ve
[N]T {P}dV [N]T {p/ }dF . (2.121)
V e |
F e |
В результате суммирования по отдельным элементам получим глобальную матрицу жесткости [k] и глобальный вектор нагрузки {G }
|
|
m |
|
|
[k] 6[k e ]; |
|
|
||
|
|
e 1 |
|
|
|
|
# (2.122) |
||
|
|
m |
||
|
|
|
e }. |
|
{G |
} {R} 6{G |
|||
|
|
e 1 |
|
|
|
|
|
|
|
Условие стационарности пол ной потенциальной энергии систе мы с учетом всех приведенных со отношений представляет систему линейных алгебраических уравне ний относительно составляющих перемещений узлов, которые явля ются неизвестными задачи. В мат ричной форме эта система имеет вид
[k]{,} {G |
}, |
(2.123) |
где {,}Т = [,1, …, ,n] – вектор узло вых перемещений.
Заданные по условиям задачи перемещения некоторых узловых точек (на осях симметрии, в местах закрепления конструкции) непо средственно подставляются в сис тему (2.123) в качестве известных компонентов вектора {,}.
При использовании треугольно го симплексного элемента в случае плоской задачи интегрирование, связанное с определением матрицы жесткости [ke] и вектора нагрузки {G e }, осуществляется в замкнутом
виде, поскольку матрицы [B] и [D] содержат лишь постоянные вели чины. Интегрирование выражения, содержащего вектор объемных сил {P}T = [X Y], производится по объе му элемента, а выражения, содер жащие вектор распределенной на грузки {p/} = [px py], по грани эле мента, по которой эта нагрузка
60
