Chainov_Ivashenko_Konstr_dvs_1 / Чайнов Иващенко - Конструирование ДВС

где X, Y, Z – объемные силы, отне сенные к единице объема тела (к ним относятся центробежные си лы, возникающие при вращении вала двигателя или дисков ротора турбокомпрессора);

уравнения связи между деформа циями и напряжениями, выражаю щие обобщенный закон Гука

где E, G – модули упругости мате риала соответственно первого и второго родов; −, Т – соответст венно коэффициент Пуассона и коэффициент линейного расшире ния материала; Т – изменение тем пературы при работе в рассматри ваемой точке детали по сравнению с исходным (нерабочим) состоя нием.

Граничные условия. Однознач ное решение задачи теории упруго сти предусматривает удовлетворе ние условий равновесия на границе тела – статических граничных ус ловий (рис. 2.5)

X / xl yx m zx n;

Y/ xyl y m zy n; # (2.25)

Z / xz l yz m z n,

Рис. 2.5. Напряжения в гранях элементарного тетраэдра

где X , Y/, Z/ – составляющие по верхностной силы, отнесенной к единице площади границы тела; l, m, n – направляющие косинусы внешней нормали к граничной по верхности тела.

Иногда исходными данными могут служить не статические, а кинематические граничные усло вия. В этом случае заданными яв ляются смещения граничной по верхности тела. Например, в случае осесимметричной задачи равенство нулю радиального перемещения на оси вращения.

В настоящее время в теории уп ругости и других разделах механи ки твердого деформированного те ла часто используют тензорные обозначения, что делает записи бо лее компактными. Координаты x, y, z обозначаются соответственно x1, x2, x3 или просто xi. Уравнения (2.21), (2.22), (2.23), (2.24), (2.25) записываются при этом следую щим образом:

Здесь индексы i, j последовательно принимают значения 1, 2, 3 с сум мированием по повторяющемуся

Уравнения (2.21(–2.24() можно при вести к системе трех уравнений от носительно неизвестных компонен тов вектора перемещений {,}. С этой целью, выразив с помощью соотно шений (2.21() в уравнениях (2.24() компоненты деформаций через со ставляющие перемещений и решив систему (2.24() относительно компо нентов тензора напряжений, полу ченный результат следует подста вить в уравнения равновесия (2.23(). В итоге получим систему уравнений Ляме, которая в случае изотропного тела имеет вид

деформация.

При решении системы (2.26) граничные условия (2.25() выража ют через составляющие вектора {,} перемещений. Интегрирование сис темы (2.26) при заданных кинема тических или преобразованных статических граничных условиях дает решение задачи теории упру гости в перемещениях.

Можно за неизвестные задачи принять компоненты тензора на пряжений. Так как число неизвест ных компонентов тензора напря жений в случае изотропного тела равно шести, то трех уравнений равновесия (2.23() недостаточно для их определения. Недостающие уравнения можно получить, выра зив деформации +ij через напряже ния (2.24(), и подставить +ij в усло вия совместности деформаций (2.22(). Полученная система шести дифференциальных уравнений от носительно компонентов тензора напряжений ij известна под назва нием уравнений Бельтрами Мит чела. При отсутствии объемных сил система в тензорной записи имеет вид

Знак запятой означает дифферен цирование величины 0 по пере менным, соответствующим i и j.

Как отмечалось ранее, задача, связанная с решением системы дифференциальных уравнений, на пример, (2.26) может быть замене на задачей определения функций, обеспечивающих стационарность (иногда экстремальное значение) некоторого функционала. В случае

задачи теории упругости под функ ционалом П понимается полная потенциальная энергия системы (например, детали или узла двига теля)

В уравнении (2.28) первый и второй интегралы по объему V вы ражают потенциальные энергии соответственно деформации тела и объемных сил, а третий интеграл по поверхности F – потенциальную энергию поверхностных сил.

При заданных статических и ки нематических граничных условиях (внешних силах и условиях закреп ления) действительные составляю щие u, v, w вектора перемещения таковы, что в состоянии равнове сия тела его полная потенциальная энергия стационарна, т.е. ,П = 0, где , – знак вариации.

Доказано, что стационарность функционала в положении равно весия соответствует минимальному значению. Это свойство стацио нарности и используется для опре деления значений функций пере мещений, т.е. решения исходной задачи по определению напряжен но деформированного состояния тела (детали).

2.3.1. Неупругое деформирование

В условиях постоянного повы шения мощности и жестких ограни чений по массе и габаритам двига телей при работе ряда деталей воз

можно появление зон пластической деформации. Определение напря женно деформированного состоя ния в этом случае связано с приме нением методов теории пластично сти, а при повышенных температу рах для теплонапряженных деталей двигателя – теории ползучести.

Высокие тепловые нагрузки ха рактерны для поршней, крышек (головок) цилиндров, втулок (гильз) цилиндров, клапанов, элементов турбокомпрессоров двигателей.

Вотличие от упругого поведе ния материала в этих случаях после снятия нагрузки в элементах кон струкции имеют место остаточные деформации и напряжения, опре деление которых требует при рас четах введения иных связей между деформациями и напряжениями, отличных от закона Гука.

Вобщем случае появление пла стических деформаций происходит как вследствие достижения дейст вующими напряжениями предель ных значений (предела текучести

материала т), так и вследствие ползучести в условиях повышен ных температур. Обычно принима ют, что общая деформация + равна сумме деформаций упругости е, пластичности р и деформации ползучести с: + = +e + +p + +c.

Определение напряженно де формированного состояния в элементах двигателя, находящих ся в условиях высоких механиче ских нагрузок при умеренных температурах, производится ме тодами теории пластичности, ус танавливающей связи между пла стическими деформациями и на пряжениями. При этом, как и при упругом деформировании, эта связь не зависит от времени, но зависит от истории нагруже ния. Решение задачи теории пла

стичности в общем случае связа но с огромными трудностями и, по мнению ряда крупных ученых, вряд ли вообще возможно. По

этому предложен ряд теорий, каж дая из которых основана на соот ветствующих гипотезах. Выделя ют группу деформационных тео рий, устанавливающих зависимо сти между компонентами тензо ров напряжений и деформаций, и группу теорий течения, рассмат ривающих связи между прираще ниями или скоростями деформа ций и напряжениями.

К первой группе относится наи более простая и достаточно распро страненная теория малых упруго пластических деформаций. В осно ву этой теории положены следую щие гипотезы.

1. Объемная деформация ) про порциональна среднему нормаль ному напряжению

Как следует из (2.29), связь ) и0 такая же, как в теории упруго сти. Таким образом, в результате пластического деформирования из менения объема тела не происхо дит, а меняется форма.

2. Компоненты девиатора де

формаций eij = +ij ,ij+0 пропорцио нальны компонентам девиатора на

пряжений Sij = ij ,ij 0

Зависимость интенсивности на пряжений от интенсивности де формаций, называемая диаграм мой деформирования, определяет ся экспериментально при испыта ниях на растяжение.

При одноосном растяжении i =

, + i + 1 2− 1 Таким образом, 3E

по диаграмме растяжения материа ла можно получить диаграмму де формирования.

Теория малых упругопластиче ских деформаций справедлива в условиях так называемого простого нагружения, при котором компо ненты девиатора напряжений воз растают пропорционально некото рому параметру. Уравнения теории малых упругопластических дефор маций характеризуют поведение нелинейно упругого тела.

Процесс пластического дефор мирования необратим и напряже ния в конечном состоянии зависят от пути деформирования. Связи между компонентами напряжений и деформаций в общем случае на гружения должны быть дифферен циальными. Теория пластического течения устанавливает связи между бесконечно малыми приращения ми деформаций, напряжений, са мими напряжениями и параметра ми пластического состояния.

При деформировании за преде лами упругости предел текучести упрочняющегося материала увели чивается. Разграничение области упругого и пластического дефор мирования описывается уравнени ем гиперповерхности пластичности в пространстве компонентов тензо ра напряжений

Вид зависимости (2.32) опреде ляет особенности той или иной теории пластического течения. Так, теории течения с изотропным упрочнением соответствует равно мерное (изотропное) расширение поверхности пластичности. В этом случае принимается ряд гипотез.

1.Пропорциональность объем ной деформации среднему нор мальному напряжению в соответст вии с уравнением (2.29).

2.Пропорциональность компо нентов девиатора приращений пла

стических деформаций d+ ijp компо

нентам девиатора напряжений Sij. 3. Интенсивность напряжений

является функцией интеграла от интенсивности приращения пла стических деформаций d+ip , не за

висящей от типа напряженного со стояния

где d+ip – интенсивность прираще

ний пластических деформаций, ко торая определяется по формуле, аналогичной (2.31) с заменой в по следней компонентов деформаций на приращения компонентов де формаций.

В случае одноосного растяженияi = , d+ip + p и функция Ф опре деляется по диаграмме растяжения.

Компоненты приращений пла стической деформации, являющие ся функциями компонент напря жения, должны удовлетворять ус ловию пластичности (2.32), что при использовании множителей Ла гранжа d приводит к соотноше нию

Соотношение (2.34) выражает так называемый ассоциированный закон течения. Согласно второй ги потезе

где d 1 d+ip . 2 i

Приращения полных деформа ций складываются из упругой и пластической составляющих. Пер вая представляется в соответствии с формулой (2.24() в виде

d+ eij 1 [(1 −)d ij ,ij 3−d 0 ].

E

Приращения пластических де формаций с использованием соот ношения (2.35) и выражения, ана логичного (2.31), для определения d+ip представляется в виде

Если приращения пластических деформаций значительно превос ходят приращения упругих дефор маций, последними пренебрегают. Используя понятие скорости де формации 2ij, можно записать

2 ij 3 2 i ( ij , ij 0 ), (2.37) 2 i

где 2i – интенсивность скорости де формаций.

В случае простого нагружения теория течения совпадает с теорией малых упруго пластических дефор маций.

2.3.2. Приближенные методы определения напряженно деформированного состояния

при пластическом деформировании

Так как точное решение упруго пластических задач, как правило, невозможно, то приближенные ме тоды решения имеют особое значе ние, являясь по существу основ ным инструментом в расчетной практике.

Но прежде чем рассматривать пути решения упругопластической задачи, необходимо остановиться на условиях начала пластического деформирования в элементах кон струкции. В случае одноосного на пряженного состояния началу пла стического деформирования соот ветствует достижение действую щим напряжением предела текуче сти т материала. В случае многоос ного напряженного состояния су ществует несколько условий кри териев начала пластического де формирования.

Наиболее часто используется ус ловие Максвелла Хубера i = т, которое также называют энергети ческим условием начала пластич ности. Согласно ему пластические деформации возникают при дости жении интенсивностью напряже ний i предела текучести при рас тяжении т.

Другим достаточно распростра ненным является условие крите

рий Треска–Сен Венана 1 3 = = т, которое также называют усло вием начала пластичности наи большего касательного напряже ния. Как показали эксперименты, условие Максвелла Хубера лучше согласуется с опытными данными, чем условие Треска–Сен Венана, но различия невелики.

Для расчета полей перемеще ний, деформаций и напряжений в условиях пластичности широко ис пользуются вариационные методы, а также методы, сводящие решение упруго пластической задачи к ре шению ряда упругих задач с помо щью последовательных приближе ний. Одним из распространенных и хорошо зарекомендовавших себя в расчетной практике является ме тод переменных параметров упру гости. При применении теории ма лых упруго пластических деформа ций связь деформаций и напряже ний принимается в виде обобщен ного закона Гука (2.24), но пара метры упругости, обозначаемые Е*, G*, −*, являются переменными в различных точках тела, будучи за висимыми от напряженного сос тояния

Для несжимаемого тела − = 1/2, и тогда

E * 3G * i + i ; −* 1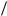2. (2.39)

На рис. 2.6 схематично пока зан процесс последовательных приближений при решении упру го пластической задачи. Сначала в

Рис. 2.6. Схема расчета по методу переменных параметров упругости

нулевом приближении принимает ся, что E0* E ; G0* G ; −*0 − и ре

шается упругая задача. При этом находятся деформации (+ij)0 и на пряжения ( ij)0 нулевого приближе ния.

По формулам (2.31) вычисляют ся интенсивности деформаций (+i)0 и напряжений ( i)0 нулевого при ближения, чему соответствует точ ка 0 на (рис. 2.6), где представлена заданная для рассматриваемого ма териала диаграмма деформирова ния. В первом приближении вели чина 3G, равная тангенсу угла на клона луча точки 0, заменяется на 3G1* *i 0 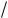+ i 0 , при этом интенсив

ность напряжений *i 0 определяет ся по кривой деформирования со ответственно +i0. Далее по форму лам (2.38) определяются значения E1* и −*1 первого приближения, ко

торые, вообще говоря, будут раз личными в различных точках тела. Используя найденные значения E1*

и −*1 , решают упругую задачу по оп

ределению (+ij)1 и ( ij)1 первого при ближения. По формулам (2.31) вы

числяются интенсивности дефор маций (+i)1 и напряжений ( i)1 пер вого приближения, чему соответст

ближения, а затем (+ij)2 и ( ij)2 вто рого приближения. Расчет закан чивается, когда разница +ij и ij по следующего и предыдущего при ближений не будет превышать на перед заданную величину. Практи ка расчетов показывает, что про цесс обычно быстро сходится и достаточно трех, а иногда и двух приближений.

2.3.3. Ползучесть

Ряд основных деталей двигателя, в том числе детали цилиндропорш невой группы, работают при повы шенных температурах. В этих усло виях проявляются такие свойства конструкционных материалов как ползучесть и длительная прочность. В обоих случаях существенным яв ляется время работы детали. Чистая ползучесть (последействие) связана с возрастанием пластических де формаций при неизменных нагруз ках. Если перемещения точек тела остаются неизменными, то со вре менем изменяются напряжения и имеет место чистая релаксация. Обычно оба процесса происходят одновременно, называясь ползуче стью. Сопротивляемость материала ползучести оценивают пределом ползучести – величиной напряже ния, при котором деформация пол зучести за определенное время дос тигает заданной величины.

Длительная прочность характе ризуется зависимостью предела

прочности материала от времени работы.

Ползучесть проявляется у угле родистых сталей и чугунов при температуре свыше 300 С, а у алю миниевых сплавов – свыше 100 С. При этом происходит понижение модуля упругости, пределов текуче сти т и прочности вр материала.

Для сохранения прочностных характеристик при высоких темпе ратурах стали легируют никелем, хромом и другими элементами. В особых случаях применяют жаро прочные сплавы на никелевой ос нове.

Процесс ползучести при посто янном во времени напряжении представлен на (рис. 2.7). Различа ют упругое и пластическое после действие. В первом случае после разгрузки – линия ВС на (рис. 2.7), деформации уменьшились бы до нуля; в случае пластического по следействия они, затухая со време нем, сохраняются – линия CD на (рис. 2.7).

В основе расчетов на ползучесть лежат данные экспериментов при одноосном напряженном состоя нии на образцах при постоянной во времени нагрузке и температуре, представленные в виде кривых ползучести на (рис. 2.8). В первой стадии ползучести за счет механи

Рис. 2.7. Кривая, иллюстрирующая пластиче ское последействие

Рис. 2.8. Кривая ползучести:

I–III – стадии

ческого упрочнения скорости де формации ползучести 2 c d+ c 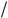d

уменьшаются до скорости 2 cmin , ко

торая сохраняется на протяжении второй стадии. Первая и особенно вторая стадии представляют наи больший интерес с точки зрения длительности работоспособности материала в условиях ползучести. В третьей стадии, заканчивающей ся разрушением, скорость ползуче сти возрастает вследствие или об разования шейки (вязкое разруше ние образца), или из за образова ния внутренних трещин (хрупкое разрушение образца). С ростом на пряжения и температуры продол жительность второй стадии умень шается.

Минимальная скорость ползу чести 2 cmin зависит от напряжения

и температуры Т

Существуют различные пред ставления функции Q( ). Чаще других используется выражение

где k и n – коэффициенты, завися щие от температуры и определяе мые экспериментально.

Для жаропрочных сталей n ко леблется в пределах 3–6. Диапа зон изменения k значительно ши ре. Так, для стали ЭИ 69 (45Х14Н14В2М) k меняется от 2,0310 10(1/МПа)n/ч при 600 С до 1,24310 8(1/МПа)n/ч при 700 С.

Деформация ползучести +с опре деляется по формуле

где Q – функция напряжения, на пример (2.41); %( – функция време ни; ) – функция температуры.

Деформации ползучести явля ются, как правило, необратимыми. Поэтому при расчетах на ползу честь для неодноосного напряжен но деформированного состояния используется ряд приведенных вы ше гипотез теории пластичности. Практические расчеты проводят с помощью так называемых техниче ских (простейших) теорий ползуче сти. Последние предполагают на личие соотношений (уравнений), описывающих процесс деформиро вания материала во времени, в том числе при переменных режимах ра боты. Технические теории форму лируются для одноосного напря женного состояния с последующим обобщением применительно к не одноосному напряженно деформи рованному состоянию.

Во многих случаях при постоян ных нагрузках ползучесть можно считать установившейся. При этом часто используется наиболее про стая из технических теорий – тео рия старения.

В случае одноосного напряжен ного состояния при заданной тем пературе предполагается существо вание зависимости между дефор мацией +, напряжением и време нем :

При постоянных значениях на пряжений из зависимости (2.43) получаются кривые ползучести (рис. 2.8), а при постоянных значе ниях времени – так называемые изохронные кривые. Если изохрон ные кривые подобны, они получа ются из одной кривой умножением ее ординат на величину, являю щуюся функцией времени. Зависи мость деформации ползучести от времени с учетом (2.41) представ ляется в виде

где % – функция времени и темпе ратуры.

Зависимость интенсивности де формаций ползучести + ci от интен

сивности напряжений определяет ся семейством кривых ползучести. В случае неодноосного напряжен но деформированного состояния эта зависимость может быть пред ставлена в соответствии с форму лой (2.44) при замене +c и интен сивностями + ci и i :

С другой стороны, зависимость компонентов деформаций ползуче сти + cij от компонентов девиатора

напряжений Sij имеет вид

Добавляя к деформациям ползу чести + cij упругие деформации + eij , с

учетом несжимаемости можно за писать выражение полной дефор мации +ij

где в случае использования степен ной зависимости (2.45) +i имеет вид

Теория старения не может опи сать ступенчатое нагружение, так как в момент изменения напряже ния деформация ползучести в соот ветствии с этой теорией должна бы иметь разрыв, чего нет на самом деле.

Однако, как показывает расчет ная практика, во многих случаях при не слишком сильном измене нии нагрузки результаты расчетов по теории старения вполне удовле творительны.

Как и в случае теории пластич ности в случае ползучести более точные результаты дает теория те чения, предполагающая существо вание определенной зависимости при заданной температуре между напряжением, скоростью деформа ции ползучести 2с и временем

При этом часто используется степенная зависимость скорости деформации ползучести от напря жения

Во второй стадии ползучести (рис. 2.8), когда скорость ползуче сти 2 c + cmin , параметр В = k. Зави симость (2.50) обобщают на случай изменения напряжений во време ни. В случае неодноосного напря женно деформированного состоя ния выражение (2.49) принимает вид

Связь компонентов скоростей деформаций ползучести с компо нентами девиатора напряжений выражается зависимостью типа (2.46), а именно

Добавляя к компонентам скоро сти деформаций ползучести 2 cij ско

рости упругих деформаций 2 eij , с

учетом несжимаемости можно за писать

Точка означает производную по времени.

Интегрирование уравнения (2.51) при = const дает семейство кри вых ползучести в виде (2.44). При этом кривые геометрически подоб ны. Зависимости (2.51), (2.52) и (2.53) являются основными соот ношениями при расчетах ползуче сти по теории течения с изотроп ным упрочнением.

Уравнения установившейся ползучести по форме имеют боль шое сходство с уравнениями де формационной теории пластично сти. Отмечается, что формально первые можно получить из вторых, если в последних пренебречь упру гой и термической деформациями, по сравнению с пластической де формацией, а компоненты + ijp , в

свою очередь, заменить на компо ненты скорости деформации пол зучести 2 cij . Таким образом, для ре

шения задач установившейся пол зучести могут быть применены ме тоды решения задач пластичности,