scherbo-sp2

В случае объемного напряженного состояния при σ1 > σ2 > σ3 наи- большее касательное напряжение определяется, как известно, полуразно- стью максимального и минимального главных напряжений:

Для плоского напряженного состояния условие (11.8) после подста- новки в него соответствующих выражений главных напряжений запишется в виде

Основной недостаток третьей теории состоит в том, что в случаях объемного напряженного состояния ею не учитывается влияние главного напряжения σ2.

Теория наибольших касательных напряжений лучше всего подтвер- ждается опытами с пластичными материалами, одинаково сопротивляю- щимися как растяжению, так и сжатию. Она достаточно широко использу- ется при оценке их прочности.

11.3. Энергетическая теория прочности

Энергетическая теория основывается на предположении о том, что

количество удельной потенциальной энергии деформации, накопленной к моменту наступления предельного напряженного состояния в материале, одинаково как при любом сложном напряженном состоянии, так и при простом растяжении.

При построении данной теории первоначально была предложена ги-

потеза, согласно которой за причину наступления предельного напряжен- ного состояния принималась полная удельная потенциальная энергия, дос- тигающая своего наибольшего значения.

91

Условие, отвечающее такой гипотезе, записывается в следующем виде:

где U – полная удельная энергия, которую для общего случая объемного напряженного состояния определяют по известной формуле

U0 – предельное значение энергии, определяемое из опыта на про- стое растяжение. Формула для ее вычисления легко получается, если в

Указанная гипотеза, однако, не оправдалась на опыте и поэтому ос- нованная на ней теория не нашла применения на практике.

Так, например, эта теория не подтверждается на опыте с всесторон- ним гидростатическим давлением, при котором, как уже говорилось вы- ше, разрушение практически не наступает.

Таким образом, энергия, соответствующая изменению объема вслед- ствие всестороннего сжатия, не может служить критерием прочности.

В предложенной новой энергетической теории за исходную была принята гипотеза, согласно которой за причину наступления предельного напряженного состояния принимается не вся удельная энергия, а лишь та ее часть, которая накапливается вследствие изменения формы куби- ка с ребром, равным единице.

Как видно, новая энергетическая теория связывается с развитием только пластических деформаций, которые, как известно, характеризуются изменением формы тела, но не сопровождаются изменением его объема.

Условие, которое должно соблюдаться при применении данной тео- рии, выражается неравенством

Для общего случая напряженного состояния непосредственное вы- числение энергии, идущей на изменение формы, вызывает затруднение. Поэтому величину Uф находят, пользуясь выражением

92

UФ – энергия, затрачиваемая на изменение объема.

В общем случае объемного напряженного состояния деформацию можно разделить на две: 1) деформацию, связанную только с изменением объема, и 2) деформацию, соответствующую только изменению формы.

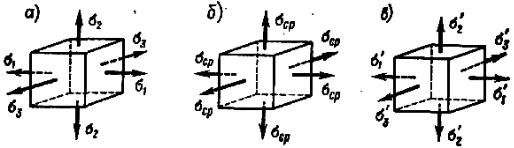
Для этого представим заданное напряженное состояние (рис. 11.2, а), определяемое главными напряжениями σ1 σ2, σ3, в виде суммы двух на- пряженных состояний (рис. 11.2, б, в). Пусть первое из них соответствует гидростатическому растяжению (сжатию), при котором по всем граням кубика действуют одинаковые средние напряжения

Так как в этом случае длины всех ребер кубика изменяются на оди- наковую величину, то форма кубика не меняется, а меняется только его объем.

93

Для определения энергии UV подставим в формулу (а) вместо σ1, σ2 и σ3 напряжения σср. Тогда

где σ0 – предельное напряжение, найденное из опыта при простом рас- тяжении.

В данной теории σ0 принимается равным пределу текучести σТ. Расчетная формула, отвечающая условию (и), запишется в виде

где R – расчетное сопротивление при растяжении.

При плоском напряженном состоянии, заменяя в формуле (11.18) со- ответствующие главные напряжения их выражениями через σх, σу и τху, по- лучим

Энергетическая теория, так же как и третья, хорошо подтверждается в опытах с пластичными материалами и широко применяется на практике.

94

Для пластичных материалов указанные теории устанавливают критерии, определяющие условия возникновения пластических деформаций в мате- риале. Поэтому неравенства (11.7) и (11.12), основанные на этих теориях,

называют иногда условиями пластичности.

Применим энергетическую теорию для теоретического определения предела текучести при чистом сдвиге. В этом случае σ = 0, τ = τT и усло- вие текучести выразится формулой

Отсюда

Аналогично по третьей теории получим τТ = 0,5σТ .

При изучении чистого сдвига в М-4 указывалось, что для многих ма- териалов экспериментально устанавливаемая зависимость между τТ, и σТ выражается соотношением (4:4). Это соотношение совпадает с (11.22). Та- ким образом, в случае чистого сдвига энергетическая теория несколько лучше согласуется с экспериментом, чем третья теория.

11.4. Теория прочности Мора

Во всех рассмотренных выше теориях в качестве гипотезы, устанав- ливающей причину наступления предельного напряженного состояния, принималась величина какого-либо одного фактора, например, напряже- ния, удлинения, энергии.

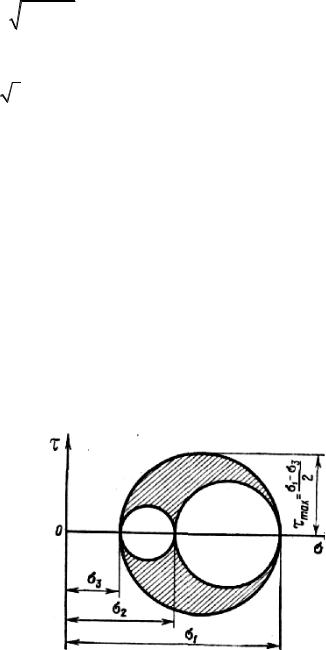
В теории Мора в отличие от изложенных теорий не рассматриваются отдельные гипотезы, а на основе экспериментальных данных уста- навливается определенная зависи- мость прочностных свойств мате- риала от вида напряженного со- стояния. Для получения и обосно- вания такой зависимости использу- ют предложенные Мором круги на- пряжений. Для объемного напря- женного состояния, как известно, строят три круга (рис. 11.3). Однако

здесь на основе имеющихся опытов

Рис. 11.3

не учитывают влияние напряжений σ2 и считают с некоторым приближением, что прочностные свойства ма-

териала связаны только с напряжениями σ1 и σ3. Поэтому из трех кругов

95

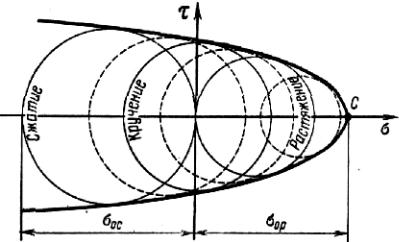
рассматривают лишь один – наибольший. Этот круг Мор назвал главным кругом.

Вслучае когда напряжения σ1 и σ3 отвечают предельному напря- женному состоянию материала, соответствующий им главный круг приня- то называть также предельным.

Вкачестве примера на рис. 11.4 изображены три предельных круга для материала, который был испытан на растяжение, сжатие и кручение. При этом предельные напряжения при сжатии, которые будем обозначать

σос, оказались больше, чем при растяжении σор, т. е. σоc > σор.

Рис. 11.4

Если провести огибающую для этих кругов, которую называют пре- дельной огибающей, то в общем случае она будет кривой, которая пересе- чет ось σ в некоторой точке С.

Эта точка соответствует всестороннему растяжению с предельным напряжением, определяемым абсциссой точки С (рис. 11.4). Круг Мора в этом случае обращается в точку ввиду того, что напряжения σ1, σ2 и σз рав- ны между собой.

Таким образом, если имеется несколько предельных кругов и их оги- бающая, то можно принять, что напряженное состояние, главный круг ко- торого касается огибающей, будет также предельным.

На рис. 11.4 изображено пунктиром семейство предельных кругов с различными сочетаниями главных напряжений. Как видно из рисунка, огибающая кругов определяет зависимость этих напряжений от вида на- пряженного состояния.

Получение действительной огибающей предельных кругов, постро- енных для всевозможных напряженных состояний, неосуществимо, так как для этого потребовалось бы опытным путем исследовать указанные на- пряженные состояния. Поэтому на практике действительную огибающую

96

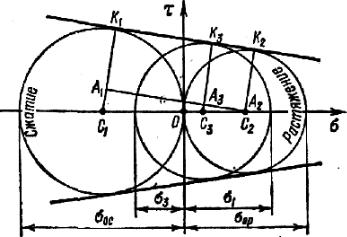
заменяют прямыми, касательными лишь к двум главным кругам, которые строят по данным опыта на растяжение и сжатие (рис. 11.5). Эти прямые являются границами области прочностных состояний. Вместе с тем они устанавливают линейную зависимость между напряжениями σ1 и σ3 всяко- го напряженного состояния, главный круг которого касается этих прямых:

Рис. 11.5

Зависимость (11.23) получается на основе простых геометрических соотношений, вытекающих из подобия треугольников А3С3С2 и А1С1С2 (рис. 11.5). Рассматривая эти треугольники, можно записать

Подстановка значений (б) в выражение (а) приводит после неслож- ных преобразований к выражению (11.23). Так как последнее должно быть справедливо и для случаев растяжения и сжатия, то можно определить ко- эффициенты а и b для произвольного сочетания σ1, и σ3, не прибегая к ука- занному преобразованию.

97

Так, при растяжении σ3 = 0 , а σ1 = σор. Введя эти значения напряже-

ний в выражение (11.23), найдем, что a = σор.

При сжатии σ1 = 0 и σ3 = −σос. Следовательно, имеем

σор − bσос = 0,

откуда

b= σор .

σос

Таким образом, выражение (11.23) принимает следующий вид:

σ1 = σср + σσор σ3, (в)

ос

или

где R – расчетное сопротивление при растяжении.

Коэффициент K позволяет учитывать различные сопротивления ма- териала растяжению и сжатию. Если эти сопротивления одинаковы по величине, то коэффициент K = 1, а касательные к главным кругам становятся параллельными оси σ (рис. 11.6). Условие (11.24) в этом случае будет таким же, как и для третьей теории прочности. Следовательно, оно применимо как для хрупких, так и для пластичных материалов. При этом для хрупких материалов вместо σор и σос берутся соответствующие пределы прочности, а для пластичных – пределы текучести.

Рис. 11.6

В заключение следует отметить, что теория Мора дает наиболее дос- товерные результаты для напряженных состояний, круги которых занимают положение в промежутке между главными кругами растяжения и сжатия.

98

М-12. ОСНОВЫ РАСЧЕТА ТОНКОСТЕННЫХ СТЕРЖНЕЙ ОТКРЫТОГО ПРОФИЛЯ

12.0. Введение в модуль

Модуль содержит следующие структурные элементы:

1.Основные понятия.

2.Свободное кручение тонкостенных стержней.

3.Стесненное кручение и его особенности.

4.Зависимости между деформациями стержня и перемещениями его точек

5.Закон распределения нормальных и касательных напряжений в се- чении стержня.

6.Расчетные формулы для напряжений и соответствующих им внутренних силовых факторов.

7.Дифференциальное уравнение угла закручивания стержня и его интегрирование.

8.Вычисление геометрических характеристик.

8.1.Определение положения центра изгиба А.

8.2.Определение главной секториальной нулевой точки М0.

8.3.Техника вычисления геометрических характеристик.

9.Общий случай действия сил на тонкостенный стержень.

Цель модуля – изучить методику расчета прочности стержней откры- того профиля.

12.1. Основные понятия

Тонкостенными называют стержни, длина которых значительно пре- вышает основные размеры b или h поперечного сечения (в 8 – 10 раз), а последние, в свою очередь, значительно превосходят (также в 8 – 10 раз) толщины стенок δ (рис. 12.1, а).

Рис. 12.1

При построении расчетной схемы тонкостенного стержня рассматри- вают его «срединную» поверхность, которая проходит через середину эле-

99

ментов, образующих стержень (рис. 12.1, б). След срединной поверхности в плоскости поперечного сечения образует профиль сечения.

Тонкостенные стержни имеют широкое применение в строительных конструкциях.

По очертанию поперечного сече- ния различают два типа стержней:

1) стержни с закрытым профилем

(рис. 12.2, а); 2) стержни с открытым профилем

(рис. 12.2, б).

Главной особенностью тонкостен- ных стержней является то, что у них при нагрузках, создающих закручива- ние, поперечные сечения в процессе де- формации не остаются плоскими. Про- исходит так называемая депланация се- чений, которая связана с перемещения-

ми точек из плоскости поперечного сечения вдоль оси стержня.

Встержнях с открытым профилем происходит значительная депла- нация сечений, что существенно отражается на условиях их работы под на- грузкой. Теория расчета тонкостенных стержней наиболее полно разрабо- тана проф. В.3. Власовым. Основы его теории для стержней открытого профиля и излагаются в настоящем модуле.

Встержнях с закрытым профилем депланация сечений значительно меньше и ее влияние сравнительно невелико.

Теория расчета стержней закрытого профиля, разработанная проф. А.А. Уманским, здесь не излагается.

12.2. Свободное кручение тонкостенных стержней

Свободным кручением называется такое кручение, при котором де- планация всех поперечных сечений стержня будет одинаковой.

Так, на рис. 12.3, а, б показан стержень, нагруженный на концах моментами и работающий в условиях свободного кручения. В таком стерж- не расстояние между двумя произ- вольными точками m и n, лежащими на любой образующей, до и после деформации остается неизменным.

Отсюда вытекает, что на любом участке стержня все продольные во-

100