
2619
.pdf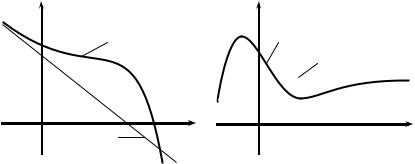
С примерами асимптот мы встречались при изучении пределов
функции (раздел 1). Напомним, что если lim f (x) = b, то пря-
x→+∞
мая y = b является асимптотой графика y = f (x) (при x → +∞), эта асимптота параллельна оси Ox и называется горизонталь ной асимптотой (см. рис. 2.15). Аналогично, прямая y = b
является асимптотой графика y = f (x) |
при x → −∞, если |
|||||||||||
lim f (x) = b (рис. 2.14). |
|
|
|
|
|
|
|
|
||||
x→−∞ |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
||||||
|
|
|
|
|
y |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
y =f(x) |
|
|
|
y =f(x) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Асимптота |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
x |
|
0 |
x |
|
Асимптота |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.14 |
|
|
|
Рис. 2.15 |
|
Рассмотрим асимптоты, параллельные оси Oy. Они на-
зываются вертикальными асимптотами.
Пусть для функции f (x): |
|
|
|
lim |
f(x) = ∞ или |
lim |
f(x) = ∞, |
x→x0 −0 |
x→x0 +0 |
||
тогда из определения асимптоты следует, что прямая x = x0
− асимптота. Очевидно и обратное, если прямая x = x0 является асимптотой, то хотя бы один из пределов,
lim |
f(x), |
lim |
f(x), |
x→x0 −0 |
x→x0 +0 |
||
является бесконечным (см. рис. 2.16, 2.17).
81
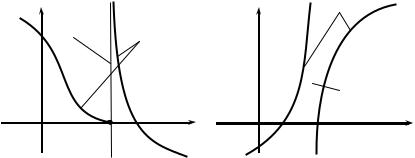
Следовательно, для отыскания вертикальных асимптот нужно найти такие значения x0, односторонние пределы в которых равны бесконечности.
|
|
|
|
|
|
|
|
|
|
|
|
|
y = f(x) |
|
|
y |
|
|
|
|
|
|
|
|
y |
|
|
|
|||
|
Асимптота |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y =f(x) |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Асимптота |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||
x0 |
0 |
|
|
|
|
||||||||||
|
|
x |
|
x0 |
|
|
x |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.16 |
|
|
|
|
|
|
|
Рис. 2.17 |
|
|||||
.
Пример 1. Найти вертикальные асимптоты для графика
1 |
|
|
|
||
функции y = |
|
. |
|
|
|
x − 2 |
1 |
|
|||
Решение. Функция f (x) = |
определена и непрерывна |
||||
x − 2 |
|||||
|
|
|
|
||
во всех точках числовой оси, за исключением точки x0 = 2, в которой функция терпит разрыв,
lim |
|
1 |
= –∞, |
|
lim |
1 |
|
= +∞. |
|
||||||||
|
x − 2 |
|
x − 2 |
|
|||||||||||||
x→2−0 |
|
|
|
|
|
|
x→2+0 |
|
|
|
|
||||||
Следовательно, прямая x |
= 2 является вертикальной |
||||||||||||||||
асимптотой для графика y = |
|
|
1 |
|
. |
|
|
|
|
|
|
|
|||||
x − 2 |
|
|
|
|
|
|
|
||||||||||
Кроме того, |
|
lim |
|
1 |
|
|
|
= 0 |
и |
lim |
|
1 |
|
= 0, следова- |
|||
|
|
x − |
2 |
|
|
x − 2 |
|||||||||||
|
x→+∞ |
|
|
|
|
|
|
x→−∞ |
|
|
|||||||
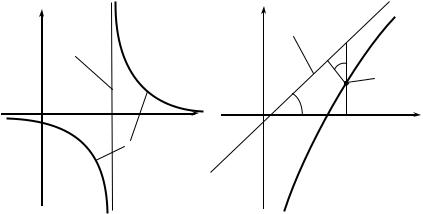
тельно прямая y = 0 является горизонтальной асимптотой при x → +∞ и при x → −∞ (см. рис. 2.18).
82
y |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Асимптота |
|
|
|
K |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Асимптота |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
y =f(x) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
α |
|
||||||||||
0 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
0 |
|
|||||||||||||||
|
|
|
|
x |
|
|
A |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|
2 |
y = |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x − 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.18 |
|
Рис. 2.19 |
|
Рассмотрим асимптоты, которые не параллельны оси Oy, |
||||
и будем называть их наклонными асимптотами. Пусть график функции y = f (x) имеет наклонную асимптоту при x → +∞, тогда ее уравнение имеет вид y = kx + b. Определим числа k и b.
Опустим из точки M(x, f(x)) графика функции перпендикуляр MN на асимптоту (см. рис. 2.19). Из определения асим-
птоты следует, что при x → +∞ длина MN → 0 ( lim |
MN = 0). |
||||
|
|
MN |
x→+∞ |
|
|
Из |
MNK имеем MK = |
, где α – угол наклона асимптоты |
|||
|
|||||
|
|
cosα |
|
||
к оси Ox, поэтому cosα – постоянная величина. |
Значит, |
||||
lim |
MK = 0. Так как MK = |AK – AM|, AK = kx + b, то |
||||
x→+∞ |
|
||||
MK = |kx + b – f(x)|, следовательно, |
|
||||
|
lim (f(x) – kx – b) = 0. |
(2.19) |
|||
|
x→+∞ |
|
|||
|
Итак, если прямая y = kx + b является асимптотой графи- |
||||
ка функции y = f (x), то выполняется равенство (2.19) и наоборот, если при постоянных числах k, b выполняется равенство
83
(2.19), то прямая y = kx + b является асимптотой. Из равенства (2.19), разделив бесконечно малую функцию (f(x) – kx – b) на x (а x → +∞), получим:
|
f (x) |
− k − |
b |
= 0, |
(2.20) |
||
lim |
|
|
|
||||
x |
|||||||
x→+∞ |
|
x |
|
|
|||
отсюда угловой коэффициент асимптоты:
k = lim |
f ( x) |
. |
(2.21) |
|
|||
x→+∞ |
x |
|
|
Определим коэффициент b из равенства (2.19), подставив в эторавенствозначениеk:
b = lim (f(x) – kx). |
(2.22) |
x→+∞ |
|
Итак, если прямая y = kx + b является асимптотой графика y = f(x), то k, b находятся по формулам (2.21), (2.22). Обратно, если существуют пределы (2.21), (2.22), то прямая y = kx + b есть асимптота. Если хотя бы один из пределов (2.21), (2.22) не существует, то при x → +∞ кривая не имеет асимптоты.
Аналогично решается вопрос об асимптотах при x → −∞. Заметим, что отдельно находить горизонтальные асимптоты нет надобности, они будут найдены при нахождении наклонных асимптот (при k = 0).
Пример 2. Найти асимптоты линии y = ex – x.
Решение. Функция f (x) = ex – x определена, непрерывна на бесконечном интервале (–∞, +∞), поэтому вертикальных асимптот нет.
Найдем наклонные асимптоты, для этого вычислим пре-
делы (2.21), (2.22) при x → +∞, x → −∞:
lim |
f (x) |
= lim ( |
ex |
– 1) = ∞, |
|
x |
x |
||||
x→+∞ |
x→+∞ |
|
84
так как lim |
|
ex |
= ∞ (проверьте это по правилу Лопиталя). |
||||||||||
|
x |
||||||||||||
x→+∞ |
|
|
|
|
|
|
|
|
|
||||
Отсюда следует, что при x → +∞ наклонных асимптот нет: |
|||||||||||||
lim |
|
f |
(x) |
|
= |
lim |
( |
ex |
– 1) = –1, так как |
lim |
ex |
= 0, |
|
|
|
x |
x |
x |
|||||||||
x→−∞ |
|
|
x→−∞ |
|
|
|
x→−∞ |
|
|||||
отсюда k = –1. |
|
|
|
|
|
|
|
|
|
||||
Далее, |
|
lim |
(f(x) – kx) = |
lim |
(ex – x + x) = lim |
ex = 0, |
|||||||
значит, b = 0.x→−∞ |
|
|
|
x→−∞ |
|
x→−∞ |
|
||||||
Итак, прямая |
y = –x |
есть |
наклонная |
асимптота при |
|||||||||
x → −∞ для графика функции y = ex – x.
85

II. ПРАКТИКУМ ПО ОСНОВАМ МАТАНАЛИЗА
1. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ 1.1. Множества и операции над ними
10. Для описания совокупности элементов или предметов принято использовать понятие множества. Обычно множества элементов обозначаются прописными буквами A,B,N, ... , а их элементы малыми буквами а,b,п,....
Если элемент а принадлежит множеству А, то пишут а А. Запись a А означает, что элемент а не принадлежит множеству А. Если множество не содержит ни одного элемента, то оно называется пустым множеством и обозначается знаком . Множество А называется счетным, если имеет место взаимно однозначное соответствие между элементами этого множества и элементами множества всех натуральных чисел N.
Если множество содержит конечное число элементов, то можно перечислить эти элементы в фигурных скобках {a,b,с}.
Выражение N = {1,2,3,...} обозначает множество натуральных чисел, а Z = {...,-2,-1,0,1,2,...} множество всех целых чисел.
Множество рациональных чисел обозначается отношением Q = mn , где т, п Z, п ≠ 0, когда только дробь
периодическая.
В противном случае числа иррациональные. Множество рациональных и иррациональных чисел называется множеством действительных или вещественных чисел и
обозначается через R.
Два множества А и В называются равными, если они состоят из одних и тех же элементов А = В. Если множество В содержит множество A, то множество А называется подмножеством множества В и обозначается B А или A B.
Пересечением множеств А и В называется множество, состоящее из элементов, принадлежащих и множеству А и множеству В и обозначается А ∩ В.
86

Объединением множеств А и В называется множество, состоящее из элементов, принадлежащих или множеству А или множеству В и обозначается А В.
Пусть множество А принадлежит основному множеству Е. Тогда множество элементов основного множества Е, не принадлежащих множеству А, называется дополнением
множества А до множества Е и обозначается Ā, отсюда
А Ā = Е, А ∩ Ā = .
Для любых подмножеств А и В основного множества Е справедливы соотношения: A B = Ā ∩ B , A ∩ B = A B .
20. Пусть А — множество действительных чисел. Множество А называется ограниченным сверху, если существует такое действительное число а, что для всех чисел x А выполняется х ≤ а. Наименьший элемент множества верхних граней ограниченного сверху множества А называется точной верхней гранью и обозначается sup А. Для множества А, ограниченного снизу, точная нижняя грань множества обозначается inf A. Множество А называется ограниченным, если оно ограничено сверху и снизу.
1.1. Описать перечислением элементов множество А = {x N | x2 -3x-4 ≤ 0}.
Решение. Найдем множество значений переменной х, удовлетворяющих неравенству x2 -3x-4 ≤ 0. Так как
х 2 - З х - 4 = (х + 1)(x-4) ≤ 0,
то x [-l,4]. Поскольку А есть множество натуральных чисел,
то A = {1,2,3,4}.
87
1.2. Логическая символика
10. Логическую символику обычно используют при записи математических объяснений. Рассмотрим несколько наиболее простых символов.
Для обозначения высказываний или утверждений воспользуемся прописными буквами латинского алфавита A, B, С и т. д.
Операция отрицания утверждения А обозначается «не А» или Ā.
Если высказывание составлено из двух высказываний при помощи союза «или», то оно является суммой этих высказываний (дизъюнкцией) и обозначается A В или (А+В). Если же высказывание составлено из высказываний при помощи союза «и», то оно является произведением этих высказываний (конъюнкцией) и обозначается А В или (А В).
Если из высказывания A следует высказывание В, то имеет место импликация А В. Если из высказывания А следует высказывание В, а из высказывания В следует А, то имеет место эквивалентность, которую обозначают А<=> В.
Знак общности употребляется вместо слов любой, каждый. Так, а А означает: «для любого элемента а А».
Знак существования употребляется вместо слова существует. а А означает: «существует элемент а А».
20. Основные свойства:
1.Коммутативность (переместительность)
А В = В А; A B = B A.
2.Ассоциативность (сочетательность)
А (В С) = (А В) С; A (B C)=(A B) C.
3. Дистрибутивность (распределительность)
A (B C) = (A B) (A C); A (B C) = (A B) (A C).
2.1. Используя логическую символику, записать утверждение: «число а есть точная верхняя грань множества
X».
88
Решение. То, что число а есть точная верхняя грань множества X, записывается а = sup X и означает х Х (х≤а), причем для сколь угодно малого ε справедливо условие
ε > 0 х X (х > а-ε ).
1.3. Понятие о функции
10. Если каждому значению одной переменной х по некоторому правилу ставится в соответствие определенное значение другой переменной y, то говорят, что между переменными существует функциональная зависимость y=f(x).
Переменную х называют независимой переменной или аргументом, а у — функцией. Функция может задаваться аналитически, графически и таблично.
Если функция задана уравнением, неразрешенным относительно y, то говорят, что функция задана неявно, и записывают f (x,y) = 0.
Если соответствующие друг другу значения x и y выражены через третью переменную (например, t), называемую параметром, то говорят, что функция задана параметрически, и записывают
x = f (t),
y =ϕ(t).
Функция может быть задана также различными аналитическими выражениями на разных участках, например функция Дирихле
χ(x) =1, |
если x рационально, |
|
|
χ(x) = 0, |
если x иррационально. |
|
||
или «сигнум x» |
sgn x |
=1, если x > 0; |
|
||
|
|
|
|
sgn x = −1, если x < 0; |
|
sgn 0 = 0.
89
20. Если каждому значению у ставится в соответствие одно или несколько значений х, то этим определяется однозначная или многозначная функция x=ϕ (y), которая называется
обратной функцией для функции у = f (х). Так для функции у = а x обратной функцией будет х = log a у. В этом случае обратная функция является однозначной. Для функции у = х 2
обратная функция будет двухзначной х = ± y .
Для обратных функций справедливы соотношения:
ϕ (f(x))=x; f(ϕ (y))=y.
Пусть каждому значению переменной х ставится в соответствие определенное значение переменной u=ϕ (x), а
каждому уже определенному значению и ставится в соответствие определенное значение y = f(u), тогда соответствие между значениями х и y имеет вид y = f(ϕ (x)) и
определяет у как сложную функцию от х, т. е. функцию от функции.
30. Функция y = f(х) называется четной, если при изменении знака аргумента на противоположный значение функции не меняется, т. е. f (х) = f (- х). График четной функции симметричен относительно оси ординат.
Функция называется нечетной, если при изменении знака аргумента на противоположный численное значение функции не меняется, а знак функции меняется на противоположный, т.е. f (-x) = - f (х). График нечетной функции симметричен относительно начала координат.
Функция называется периодической, если существует такое число T, называемое периодом функции, что значение функции не меняется при прибавлении или вычитании этого числа к любому значению аргумента, т.е.
f(x)= f(x+T)= f(x+2T)=…= f(x+kT),
где k — любое целое положительное или отрицательное число. График периодической функции повторяется через равные интервалы.
90
