Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4624 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Воронежский государственный технический университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

2619

.pdf
Скачиваний:
2
Добавлен:
15.11.2022
Размер:
1.95 Mб
Скачать
☆

 

 

 

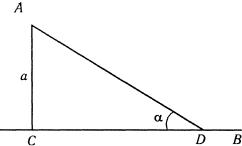
Рис. 2.42

 

 

 

 

 

 

 

 

 

Находим производную

dz

=

ma(1 − 2 cosα)

 

и приравни-

dα

 

 

 

 

 

 

 

 

 

sin 2 α

π

 

ваем ее к нулю 1 − 2 cosα = 0,

cosα =

1

,

α =

. Исследуем

 

3

 

 

 

 

 

π

 

 

2

 

 

 

функцию на экстремум при α =

 

 

по знаку второй производ-

ной:

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

d 2 z

 

2am(1 − cosα + cos2 α)

 

 

π

 

 

 

 

 

 

 

=

 

 

 

,

z′′

 

> 0.

 

 

 

 

dα 2

sin 2 α

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

Следовательно, функция имеет минимум и, чтобы доставка груза была наиболее дешевой, то шоссе следует прово-

дить под углом α = π3 .

11.13.Два самолета летят с одинаковой скоростью v км/ч,

водной плоскости, прямолинейно и под углом 60° друг к другу, в некоторый момент один самолет пришел в точку пересечения линий движения, а второй не дошел до нее на a км.

Через сколько времени расстояние между самолетами будет наименьшим и чему оно равно?

211

Рис. 2.43

Решение. По условию, когда один самолет был в точке А, другой был в точке В, отсюда АВ = а (рис. 2.43). За время t самолеты пройдут путь, соответственно: АА1 = vt, ВВ1 = vt. Отсюда АВ1 = АB - ВВ1 = a - vt. Пусть расстояние между самолетами A1B1=S, тогда по теореме косинусов получим

 

 

S = ((vt)2 + (a − vt)2

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

− 2vt(a − vt) cos120 )

2

 

 

 

 

 

или

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

S = (v2t 2 − 2vt + a2 )

2

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

•

 

 

 

 

 

2v

2

t − av

 

 

 

 

 

 

 

 

Найдем производную S =

 

 

 

 

 

 

 

 

 

и прирав-

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2(v2t 2

− avt + a2 )

2

 

 

няем ее

к

 

нулю: 2v2t −av =0,

 

t =

 

a

. Вторая производная

 

 

2v

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

••

 

2v

2

(v

2

t

2

− avt + a

2

) −

(2v

2

t

− av)

2

 

 

 

 

 

 

a

 

 

 

 

 

 

 

2

 

 

 

при t =

 

 

 

S

=

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

больше ну-

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

2v

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2(v2t 2 − avt + a2 ) 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ля, следовательно, функция имеет минимум.

Наименьшее расстояние между самолетами через t = 2av

 

 

 

 

 

 

 

 

1

 

 

 

2

a2

 

a

 

2

 

2

 

3

 

 

 

 

 

− av

 

+ a

 

 

=

 

a

 

 

2

 

 

 

будет равно S = v

 

4v

2v

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

212

 

 

 

 

 

 

11.14. Стоимость топлива для судна пропорциональна кубу его скорости. При какой скорости судна общая сумма расходов на 1км пути будет наименьшей, если при скорости 20 км/ч расходы на топливо составляют 40 руб.в час, а остальные расходы 270 руб. в час?

Решение. Обозначим стоимость топлива через q, тогда q = kv3, где к - коэффициент пропорциональности найдем из

условия 40 = k 203 , к = 0,005.

Общая стоимость плавания судна в течение часа в рублях находится по формуле Q = a + q = a + kv3 , где а = 270руб. остальные расходы. Затраты на 1км пути выразятся в виде функ-

ции u(v) = Q

= a

+ kv2 .

 

 

 

 

 

 

 

 

v

 

v

 

 

 

 

 

 

 

 

 

Для нахождения общей наименьшей суммы расходов на

 

 

 

 

 

 

 

 

′

 

a

 

 

1км пути вычисляем производную u

= − v2 + 2kv и приравни-

 

ваем ее к нулю

2kv3 − a = 0 . Подставляя числовые значения,

получим

v

=

30

км/ч.

 

Вторая

производная

u′′ =

2a

540

 

 

 

 

 

 

 

 

+ 2k

=

 

+ 0,01

= 0,03 > 0

 

 

 

 

 

v3

27000

 

 

 

 

 

следовательно, при скорости судна v = 30 км/ч общая стоимость расходов на 1км пути будет наименьшей и составит

u= 27030 + 0,005 302 =13,5 руб.

2.12.Направление выпуклости кривой. Точки перегиба

Если кривая расположена в некотором интервале ниже любой своей касательной, то она называется выпуклой вверх, а если кривая расположена выше любой своей касательной, то она называется выпуклой вниз.

Функция у = f(x) выпукла вверх, если f ′′(x) < 0 и выпукла вниз, если f ′′(x) > 0 . Если f ′′(x0 ) = 0 в некоторой точке x0,

213

бесконечна или вовсе не существует и f ′′(x) меняет знак при

переходе через точку x0, то график функции в точке x0 имеет перегиб. Если же f ′′(x) сохраняет знак, то перегиба нет.

Чтобы исследовать кривую у = f (x) на направление вы-

пуклости, надо найти вторую производную и приравнять ее к нулю f ′′(x) = 0 . Корни этого уравнения, а также возможные

точки разрыва функции и второй производной разбивают область определения функции на ряд интервалов. Выпуклость на каждом из интервалов определяется знаком второй производной.

12.1. Исследовать на направление выпуклости и найти

точки

перегиба

кривой:

а)

y = 3x4 −8x3 +6x2 −9 ;

6) y = x4

− x +1.

 

 

 

Решение. а) Функция определена для любого значения х. Находим производные:

y′ =12x3 −24x2 +12x; y′′ = 36x2 −48x +12

и приравнива-

 

 

 

1

 

 

 

 

ем вторую производную к нулю (x −

1) x −

 

 

= 0 .

3

 

 

 

 

1

 

 

Корни этого уравнения x =1

и x

2

=

 

разбивают об-

 

 

1

 

 

 

3

 

 

 

 

 

 

 

 

 

ласть определения функции на три интервала. Определяем методом интервалов (рис.2.44) знак y′′ на каждом промежутке.

Поскольку у'' при переходе через эти точки меняет знак,

то в точках x = 13 и х = 1 функция имеет перегибы. На интер-

валах ] − ∞; 13[ и ]1;∞[ кривая выпукла вниз, а на интервале ] 13 ,1 [ выпукла вверх.

214

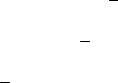
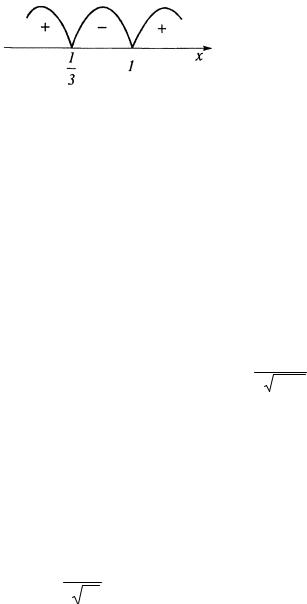
Рис. 7.44

б) Найдем вторую производную и приравняем ее к нулю: y′ = 4x3 −1; y′′ =12x2 ; 12x2 = 0; x = 0 .

При x = 0 вторая производная y′′ = 0 . Поскольку вторая

производная при переходе через точку x = 0 знака не меняет и при любом значении х положительна, то кривая на всей числовой оси направлена выпуклостью вниз.

12.2. Исследовать направление выпуклости и найти точ-

 

 

5

 

 

 

 

 

 

2

 

 

ки перегиба кривой: а) y =1 + (x −3)

3

;

 

 

 

 

б) y = x

3

;

 

в)

y =1 −

 

x3 −1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Решение. а) Находим:

y′ =

5

 

 

 

 

 

2

 

y′′ =

10

 

(x −3) 3

,

. Вто-

3

93 x −3

рая производная не существует в точке х = 3 и не обращается в нуль ни при каких значениях х. При переходе через точку х = 3 вторая производная меняет знак с минуса на плюс, следовательно, точка (3,1) является точкой перегиба. Поскольку при

x ] − ∞,3[

y′′ < 0 , то в этом интервале кривая выпукла вверх.

При x ]3, ∞[ y′′ > 0 , следовательно, кривая выпукла вниз.

 

 

 

 

 

 

 

 

2

 

−

1

 

 

 

 

 

 

 

 

 

 

 

б) Найдем вторую производную: y′ =

 

x

3 ,

3

 

′′

 

2

 

−

4

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

93 x4 . Производная у" нигде в нуль не

y

= −

9 x

= −

 

 

 

обращается. При х = 0 вторая производная не существует. При переходе через точку х = 0 вторая производная знака не меня-

215

′′

−ε),

′′

+ε) > 0,

ε > 0 . При

x ] − ∞, ∞[ y

′′

< 0 , сле-

ет: y (0

y (0

 

довательно, кривая выпукла вверх на всей числовой оси.

в) Находим точки х, в которых y′′ = 0 или не существует: y′ = ±3x2 , y′′ = ±6x , где знак плюс соответствует значе-

ниям x ] − ∞,1[ (x3 −1 < 0), а минус - x ]1, ∞[ (x3 −1 > 0) .

Поскольку при x = 0 вторая производная y′′ = 0 , а

при х = 1 не существует, то эти значения х могут быть абсциссами точек перегиба. Знак y′′ слева и справа от точек х = 0 и

х = 1 показан на рис. 2.45. Так как y′′ при переходе через точ-

ки х = 0 и х = 1

 

 

Рис. 2.45

меняет знаки, то х = 0

и х = 1 - абсциссы точек перегиба. При

x ] − ∞,0] y′′ < 0

- кривая выпукла вверх, при x ]0,1] y′′ > 0 -

кривая выпукла

вниз,

при x ]1, ∞] y′′ < 0 - кривая выпукла

вверх. Определяя ординаты точек перегиба y(0) = 0, у(0) = 1, строим кривую (рис. 2.46).

Рис. 2.46

216

2.13. Асимптоты кривой

10. Прямая y = kx + b называется наклонной асимптотой

для кривой у = f(x) при x → ±∞ , если, lim [ f (x) − (kx + b)] = 0 ,

x→±∞

т. е. если расстояние от точки кривой до прямой стремится к нулю. Параметры к и b находятся с помощью пределов

k = lim

f (x)

и b = lim ( f (x) − kx) .Если хотя бы один предел

 

x→±∞

x

x→±∞

бесконечен, то асимптот нет.

Если lim f (x) = ∞ , то кривая у = f (x) имеет горизонталь-

 

x→a

y = b.

ную асимптоту

Если lim = ∞, то кривая у = f (x) при приближении х к а

x→a

будет безгранично приближаться, уходя в бесконечность, к вертикальной прямой х = а. Прямую х = а называют вертикальной асимптотой. Как правило, это точки разрыва.

20. Если кривая задана параметрически x = ϕ(t), y =ψ (t) ,

то исследуют, нет ли таких значений параметра t, при которых функции ϕ(t), ψ (t) или одна из них обращается в бесконеч-

ность.

Уравнение наклонной асимптоты имеет вид y = kx+b, где

k = lim

ψ (t)

, b = lim(ϕ(t) − kψ (t)) , причем ϕ(t0 ) =ψ (t0 ) = ∞.

t→t0

ϕ(t)

t→t0

 

Если

при ψ (t0 ) = ∞, ϕ(t0 ) = c ,

то кривая имеет верти-

кальную асимптоту x=C. Если при

ϕ(t0 ) = ∞, ψ (t0 ) = C , то

кривая имеет горизонтальную асимптоту у = С.

30. Если кривая задана уравнением ρ = ρ(ϕ) в полярной

системе координат, то, преобразовав уравнение кривой к параметрическому виду по формулам x = ρ cosϕ = ρ(ϕ) cosϕ ,

y = ρ sin ϕ = ρ(ϕ) sinϕ , ее асимптоты находят по предыдущему правилу.

217

40. Если кривая задана уравнением F{x,y) = 0 (т. е. неявно), то для отыскания асимптот в ряде случаев удобнее представить ее в полярных координатах или перейти к параметрическому виду.

Для алгебраической кривой ∑ak i xk yi = 0 суммирование

k ,i

идет по всем целым k и i; (0 ≤ k ≤ n; 0 ≤ i ≤ n) , наклонная

асимптота у = кх +b находится подстановкой ее в уравнение кривой и приравниванием к нулю, в получившемся многочлене относительно х, коэффициентов при двух старших степенях

х.

Из решения этой системы относительно к и b находим параметры наклонной асимптоты.

Вертикальная асимптота алгебраической кривой находится из приравнивания к нулю коэффициента при старшей степени y.

13.1.Найти асимптоты кривых: а) y = x2 + 3x + 6 ;

x−1

 

б)

y =

 

 

x

 

 

 

; в )

y =

sin x

.

 

 

 

 

 

 

 

x2

−1

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

Решение. а) При x = 1 функция терпит разрыв, причем

lim

x2

+ 3x + 6

 

= −∞, а

lim

x2

+ 3x + 6

= ∞ . То

есть прямая

 

x −1

 

 

 

 

x −1

 

x→1−0

 

 

 

 

 

 

 

 

x→1+0

 

 

 

 

 

х = 1 является вертикальной асимптотой.

 

 

Находим параметры к и b наклонной асимптоты

 

 

 

 

 

x

2

+ 3x + 6

 

 

 

 

 

2

+ 3x + 6

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

k = lim

 

 

 

 

 

 

=1; b =

lim

 

 

 

 

− x = 4 .

 

 

 

x(x −1)

 

 

x −1

 

 

x→±∞

 

 

 

 

 

x→±∞

 

 

Следовательно, уравнение наклонной асимптоты имеет вид у = х + 4. График кривой и асимптоты показаны на рис. 2.47.

218

 

 

 

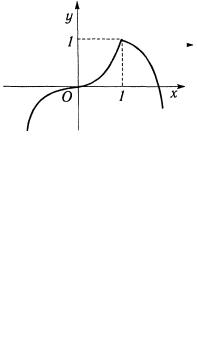
Рис. 2.47

 

 

 

 

 

б) Так как

lim

 

x

 

= ∞ , то прямые x=1 и x=-1 будут

x2 −1

x→±1

 

 

 

 

 

 

 

 

вертикальными асимптотами.

 

 

 

x

 

 

Так как при

x → ∞ предел

lim

f (x) = lim

 

= 0 , то

 

−1

 

 

 

 

 

 

 

x→±∞

x→±∞ x2

 

прямая y = 0 будет горизонтальной асимптотой.

 

 

 

Поскольку

lim

 

x

 

= 0

и b=0, то наклонных асим-

 

 

 

 

 

x→±∞ x(x2

−1)

 

 

 

 

 

 

птот нет. График функции и асимптоты показаны на рис. 2.48.

Рис. 2.48

219

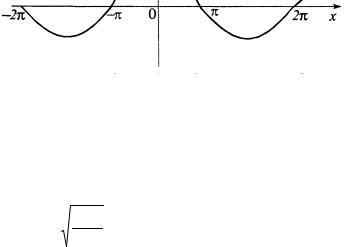
в) Функция определена на всей числовой оси х, бесконечных разрывов не имеет, поэтому не имеет и вертикальных

асимптот Определяем наклонные асимптоты:

 

 

 

k = lim

y

= lim

 

sin x

= 0, b = lim ( y − kx) = lim

sin x

= 0 ,

 

 

x2

x

x→±∞ x

x→±∞

 

x→±∞

x→±∞

 

следовательно,

y = 0

будет ее горизонтальной асимптотой.

Данная кривая бесчисленное множество раз пересекает свою асимптоту y=0, переходя с одной ее стороны на другую в точках x = kπ (k = ±1,±2,...) и неограниченно приближаясь к

ней (рис. 2.49).

Рис. 2.49

 

 

 

 

 

 

 

 

1

 

13.2. Найти асимптоты кривых: а) f (x) = e

x

;

б)

f (x) =

x3

 

;

 

 

 

 

 

x −

1

 

 

 

 

 

Решение.

 

 

 

 

 

 

а)

 

Найдем

горизонтальную асимптоту

 

1

 

 

 

1

 

 

 

lim f (x) = lim e

x

=1,

lim f (x) = lim e

x

=1,

 

 

x→∞

x→∞

 

x→−∞

x→−∞

 

 

 

следовательно, горизонтальная асимптота имеет вид у =1. Найдем теперь вертикальную асимптоту:

 

1

 

 

1

 

lim f (x) = lim e

x

= ∞,

lim f (x) = lim e

x

= 0

x→+0

x→+0

x→−0

x→−0

следовательно, x = 0 - вертикальная асимптота (рис. 2.50).

220

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности