
2619
.pdf
f (x) |
= |
f ′(c) |
. Заметим, что число c зависит от x, но если |
|
g(x) |
g ′(c) |
|||
|
|
x → x0 , то c → x0 , так как x0 < c < x. Переходя к пределу в последнем равенстве, получаем:
lim |
f (x) |
= lim |
f ′(c) |
= lim |
f ′(c) |
= lim |
f ′(x) |
. |
|||||
g(x) |
g ′(c) |
g ′(c) |
g ′(x) |
||||||||||
x→x |
0 |
x→x |
0 |
c→x |
0 |
x→x |
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|||||
Случай 2. x < 0, тогда x < x0. Функции f(x), g(x), рассматриваемые на отрезке [x, x0], удовлетворяют условиям теоремы Коши, и потому доказательство аналогично, как в случае 1. Итак, теорема Лопиталя доказана.
Пример 1. Найти lim 1 − cos 3x .
x→0 2x
Решение. Поскольку функции f (x) =1 – cos3x, g(x) = 2x удовлетворяют условию теоремы Лопиталя, то
lim |
1 − cos 3x |
= lim |
(1−cos 3x)′ |
= lim |
3sin |
3x |
= 0. |
2x |
(2x)′ |
2 |
|
||||
x→0 |
x→0 |
x→0 |
|
|
Замечание 1. Теорема Лопиталя справедлива и в том случае, когда функции f(x), g(x) не определены в точке x0, но
lim f(x) = 0 и |
lim g(x) = 0. В самом деле, если доопределить |
x→x0 |
x→x0 |
f (x), g(x), положив f (x0) = g(x0) = 0, тогда f(x), g(x) будут непрерывны в точке x0, а потому теорема Лопиталя будет при-
менима к ним.
Замечание 2. Правило Лопиталя применимо и в том случае,
когда f (x) = 0, g (x) = 0.
Действительно, введя новую переменную y =1/ x , видим, что y → 0 при x → ∞. Тогда
lim |
f (x) |
= |
lim |
f (1/ y) |
= |
lim |
f ′(1/ y) |
= |
lim |
f ′(x) |
. |
||
g(x) |
g(1/ y) |
|
g ′(1/ y) |
|
|
||||||||
x→+∞ |
|
y→0 |
|
y→0 |
|
x→∞ |
g ′(x) |
||||||
71

Теорема Лопиталя. (Раскрытие неопределенностей типа ∞ )
∞
Пусть функции f (x), g(x) дифференцируемы в окрестности точке x0, за исключением самой точки x0, причем g'(x) ≠ 0,
ипусть
f ′(x) lim ′
x→x0 g (x)
lim f(x) = ∞, |
|
lim g(x) = ∞. Если существует |
||||||||
x→x0 |
|
|
x→x0 |
|
|
|
|
|||
, то существует |
lim |
|
f (x) |
и |
|
|||||
|
g(x) |
|
||||||||
|
|
|
x→x0 |
|
|
|
||||
lim |
f |
(x) |
= |
lim |
|
f ′(x) |
. |
|||
g(x) |
|
g ′(x) |
||||||||
x→x |
0 |
|
x→x |
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
||
Отметим, что эта теорема верна для случая, когда x→∞, в этом можно убедиться, повторяя рассуждения замечания 2.
Замечание 3. Предел отношения двух функций может существовать, в то время как предел отношения их производных не существует.
Например, lim |
|
x + sin x |
= 1, а |
|
|
lim |
(x +sin x)′ |
= lim (1 + cosx) |
|||||||||||||||
|
|
|
x |
|
|
|
|
(x)′ |
|
|
|||||||||||||
x→∞ |
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
x→∞ |
||||||||||
– не существует, так как |
|
lim cosx |
|
не существует. |
|
||||||||||||||||||
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Замечание 4. Если |
|
|
f ′(x) |
|
при x |
→ x0 (x → ∞) является |
|||||||||||||||||
|
|
g ′(x) |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
неопределенностью типа |
0 |
или |
|
∞ |
|
, и |
f ′(x), |
g'(x) удовлетво- |
|||||||||||||||
|
|
∞ |
|||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ряют условиям теоремы Лопиталя, то |
|
|
|
|
′′( x) |
|
|||||||||||||||||
|
lim |
f (x) |
|
= lim |
|
|
f |
′(x) |
= |
lim |
f |
. |
|||||||||||
|
g(x) |
|
|
|
g ′(x) |
g ′′( x) |
|||||||||||||||||
x→x |
0 |
|
|
|
x→x |
0 |
|
|
|
x→x |
0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, для раскрытия неопределенностей типа 0 или
0
∞∞ иногда приходится применять правило Лопиталя несколько раз.
72
Пример 2. Найти lim |
ln x |
. |
|
|
|
||
x→0 |
ctg x |
|
|
Решение. При x → 0 и x > 0 lim lnx = ∞, |
lim ctgx = ∞, |
||
|
|
x→0 |
x→0 |
следовательно, имеем отношение двух бесконечно больших
при x → 0 и неопределенность типа |
∞ |
. Вычислим: |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
lim |
ln x |
= lim |
|
1/ x |
|
= – lim |
sin 2 |
x |
= – lim |
2 sin x cos x |
= 0. |
||||||||
ctg x |
−1 sin 2 |
|
|
x |
|
|
|
1 |
|||||||||||
x→0 |
|
|
x→0 |
x |
x→0 |
|
|
x→0 |
|
|
|
||||||||
|
Замечание 5. Теорема Лопиталя остается верной и тогда, |
||||||||||||||||||
когда lim |
|
f ′(x) |
= ∞. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
g ′(x) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x→x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
e x |
|
|
|
|
|
|
|
|
|
|
|
Пример 3. Найти |
lim |
. |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
x→+∞ x2 |
|
|
|
|
|
|
∞ |
|
|
||
|
Решение. |
Имеем неопределенность типа |
|
. Применяя |
|||||||||||||||
|
|
∞ |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
теорему Лопиталя два раза, получим: |
|
|
||||||
lim |
e x |
= |
lim |
ex |
= lim |
e x |
= ∞. |
|
x2 |
2x |
2 |
||||||
x→+∞ |
|
x→+∞ |
x→∞ |
|
||||
2.11. Возрастание и убывание функций
Теорема 1. (Достаточное условие возрастания функции)
Если функция f (x) непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b), причем f ′(x) > 0 для любого
x (a, b), то эта функция возрастает на отрезке [a, b]. Доказательство. Функция возрастает на [a, b], если
x1, x2 [a,b] (x1 < x2 → f(x1) < f (x2)).
Пусть x1, x2 – любые два числа из [a, b], такие, что x1 < x2. Докажем, что f(x1) < f(x2).
73
По теореме Лагранжа о конечных приращениях
f (x ) – f (x ) = |
f ′(с)(x |
2 |
– x ), |
|
2 |
1 |
|
1 |
|
где c удовлетворяет неравенству x1 < c < x2. По условию теоремы f ′(с) > 0, следовательно, f(x2) – f (x1) > 0, т.е.
f (x1) < f (x2). Теорема доказана.
Теорема 2. (Необходимое условие возрастания функции)
Если функция f (x) непрерывна и возрастает на отрезке [a, b], дифференцируема на интервале (a, b), то f ′(x) ≥ 0 для любого x из интервала (a, b).
Доказательство. Пусть x0 (a, b). Дадим аргументу при-
ращение x, тогда функция получит приращение |
|
|
|
|
|
|||||||||||||||||||||
f(x0 + |
|
x) – f(x0). Функция f (x) возрастает на [a, b], поэтому, |
||||||||||||||||||||||||
|
|
|
|
если x > 0, то f(x0 + |
x) – f(x0) > 0, |
|
|
|
|
|
||||||||||||||||
|
|
|
|
а если x < 0, то f(x0 + |
x) – f(x0) < 0. |
|
|
|
|
|
||||||||||||||||
В |
|
обоих |
случаях |
|
f ( x0 + |
x) − f ( x0 ) |
> 0, |
|
|
а |
|
потому |
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
f ( x0 + |
x) − f ( x0 ) |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
≥ 0, т.е. f ′(x0) ≥ 0. Теорема доказана. |
||||||||||||||||||||||
|
|
|
x |
|
||||||||||||||||||||||
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Аналогичные теоремы справедливы для убывающей |
|||||||||||||||||||||||
функции, только условие f ′(x) > 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
заменяется на условие: |
f ′(x) < 0. |
|
|
|
|
|
|
y |
|
|
|
|
|
|||||||||||||
|
|
|
Пример. Исследовать на мо- |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||
нотонность (т.е. возрастание и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = x3 −3x |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
убывание) функцию: f (x) = x3 – 3x. |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Решение. f ′(x) = 3x2 – 3 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
− 3 |
|
|
– |
|
|
|
|
|
|
|
|
1 |
|
3 |
|||||||||
=3(x |
2 |
– 1). |
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Неравенство f ′(x) > 0, |
т.е. |
|
|
|
|
|
–2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
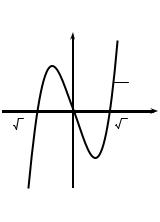
3(x2 – 1) > 0, |
справедливо дляx < –1 |
|
|
|
Рис. 2.10 |
|
|
|||||||||||||||||||
и |
для x >1. Следовательно, функция |
|
|
|
|
|
||||||||||||||||||||
74
f (x) возрастаетнаинтервалах (–∞, –1) и (1, +∞). Посколькунера-
венство f ′(x) < 0, т.е. |
3(x2 – 1) < 0 |
справедливо для x (–1, 1), то |
|||
наинтервале (–1, 1) функция f (x) убывает. |
|
|
|||
Построим график функции |
y = x3 – 3x |
(рис. 2.10), ис- |
|||
пользуя ее значения в точках: |
|
|
|
||
x1 = –1, |
x2 = 1, |
x3 = 0, |
x4 = – 3 , |
x5 = |
3 : |
f(–1) = 2, |
f(1) = –2, |
f(0) = 0, |
f(– 3 ) = 0, |
f( |
3 ) = 0. |
Заметим, что в точке x1 = –1 значение f (–1) больше, чем
значение f (x) в соседних с x1 точках. Говорят, что в точке x1 функция имеет максимум (локальный максимум). Аналогично, f(x2) < f(x) для x, близких к x2. В этом случае говорят, что в точках x2 функция имеет минимум (локальный минимум).
2.12. Экстремумы функции
Дадим точные определения точкам максимума и минимума функции. Пусть функция f (x) определена на промежутке
X и x0 X.
Говорят, что в точке x0 функция f (x) имеет максимум, если существует такая окрестность точки x0, что для любого x из этой окрестности f (x) < f (x0).
Точка x0 называется точкой минимума, если существует такая окрестность точки x0, что для любого x из этой окрест-
ности f (x) > f (x0).
Точки максимума и минимума называются точками экс-
тремума.
Замечание. Точки экстремума всегда являются внутренними точками промежутка, т.е. не могут быть его концом.
Теорема 1. (Необходимое условие экстремума)
Если функция f (x) дифференцируема в точке x0 и некоторой ее окрестности и x0 – точка экстремума, то f ′(x0) = 0.
75
Доказательство. Пусть для определенности x0 – точка максимума, тогда найдется окрестность (x0 – δ, x0 + δ) точки x0
такая |
что, |
для |
любого |
x (x0 – δ, x0 + |
δ) |
f(x) < f(x0), т.е. |
f (x0) – наибольшее значение функции f (x) |
на |
|||
интервале (x0 – δ, x0 + δ). Тогда по теореме Ферма (разд. 2.9) |
|
f ′(x0) = 0. Теорема доказана. |
f ′(x0) = 0 или |
Следствие. Если x0 – точка экстремума, то |
|
f ′(x0) не существует. |
|
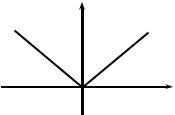
В качестве примера приведем функцию f(x) = |x| |
(рис. 2.11). |
Очевидно, что x0 = 0 является точкой минимума, так как |0| < |x| для любого x ≠ 0. А в точке x0 = 0 производной f '(0) не существует.
Если f '(x0) = 0 или f '(x0) не существует, то точку x0 будем называть критической (или подозрительной на экстремум). Критическая точка может и не быть точкой экстремума.
Теорема 2. (Первое достаточное условие экстремума)
Пусть функция f (x) определена и непрерывна в точке x0 и некоторой ее окрестности, дифференцируема в этой окрестности, за исключением, может быть, точки x0, и x0 – критическая
точка |
для |
функции |
f (x) |
|
(т.е. f ′(x0)=0 или f ′(x0) не сущест- |
y |
|||
вует). Тогда: |
1) если |
при |
x < x0 |
производная |
f ′(x) > 0, |
а для |
|
x > x0: |
f ′(x) < 0, |
то |
|
x0 – точка максимума; |
|
|
|
2) если при x < x0: |
|||
f ′(x) < 0, а при x > x0: |
f ′(x) > 0, |
||
то x0 – точка минимума.
|
|
|
y = |
|
x |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
x |
Рис. 2.11
76

Доказательство. Пусть для x < x0: f ′(x) > 0, а для x > x0: f ′(x) < 0, т.е. при переходе через точку x0 слева направо про-
изводная меняет знак с + на –. Тогда слева от x0 функция f(x) возрастает, а справа от x0 функция f(x) убывает, следовательно, x0 – точка максимума. Аналогично доказывается вторая часть теоремы.
Теорема 3. (Второе достаточное условие экстремума). Пусть функция f (x) дважды дифференцируема в точке x0
и некоторой ее окрестности и пусть |
f ′(x0) = 0. Если |
f ′′(x0) > 0, то x0 – точка минимума. Если |
f ′′(x0) < 0, то x0 – |
точка максимума.
Доказательство. Пусть f ′(x0) = 0 и f ′′(x0) > 0. Покажем,
чтоx0 – точкаминимума:
f''(x0) = |
lim |
|
f ′(x |
0 |
+ x) − f ′(x |
0 |
) |
= lim |
f ′(x |
0 |
+ |
x) |
> 0. |
||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
x |
|
|
|
|
|
x |
|
||||||
|
x→0 |
|
|
|
|
|
x→0 |
|
|
|
|||||||
Тогда |
в |
некоторой окрестности точки x0 |
выполняется |
||||||||||||||
|
|
|
f ′(x + |
x) |
|
|
|
|
|
|
|
|
|
|
|
||
неравенство |
|
|
0 |
|
|
> 0. |
Отсюда, |
если |
|
x < 0, то |
|||||||
|
|
|
x |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f ′(x0 + x) < 0, а если |
x > 0, то |
f ′(x0 + |
x) > 0, т.е. слева от |
||||||||||||||
точки x0 функция f (x) убывает, а справа – возрастает, это означает, что x0 – точка минимума. Аналогично доказывается вторая часть теоремы для f ′′(x0) < 0.
Пример 1. Исследовать на экстремум функцию f (x) = x + 4x .
Решение. Область определения функции (-∞, 0) (0, +∞), в каждом из этих интервалов функция непрерывна. Найдем f'(x) и f''`(x): f '(x) = 1 – x42 , f''(x) = x83 . Теперь найдем крити-
77
ческие точки функции, для этого решим уравнение f'(x) = 0: 1 – x42 = 0, отсюда x1 = –2, x2 = +2 – критические точки.
Используем теорему 3 для исследования критических точек,
для |
этого вычислим |
f''(x) |
в |
точках |
x1 |
и x2. |
Так как |
|||||||||||
f''(–2) = |
8 |
|
= –1< 0, то x1 |
= –2 является точкой максимума |
||||||||||||||
(−2)3 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
f |
макс |
(–2) = –2 – |
|
4 |
= –4. Для |
x : |
f''(2) = |
8 |
|
= 1 > 0, |
поэтому |
|||||||
|
|
|
||||||||||||||||
|
|
|
|
2 |
|
|
2 |
|
|
|
8 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|||||
x2 = 2 – точка минимума, |
fмин(2) = 2 + |
|
= 4. |
|
|
|||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||
2.13. Выпуклость, вогнутость графика функции, точки перегиба
Пусть f (x) – функция, дифференцируемая на интервале (a, b). Рассмотрим кривую, являющуюся графиком функции y = f (x).
Кривая, заданная функцией y = f (x), называется выпуклой на интервале (a, b), если все точки кривой лежат ниже любой ее касательной на этом интервале.
Кривая называется вогнутой на интервале (a, b), если все точки кривой лежат выше любой ее касательной на этом интервале.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
y = f(x) |
|||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yкас |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
– |
|
– |
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
x K |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1 |
1, |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
a |
|
|
x0 |
|
|
x |
b |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
Рис. 2.12 |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.13 |
|
|
|
|
|
|
|
|||||||||||||||
78
Точка кривой M0(x0, f(x0)), отделяющая выпуклую ее часть от вогнутой, называется точкой перегиба.
Кривая y = f (x) (рис.2.12) является выпуклой на интервалах (–2; –1,5) и (0; 1,5), вогнутой на интервалах (–1,5; 0) и
(1,5; 2). Точки M1(–1,5; f(–1,5)), O(0, 0), M2(1,5; f(1,5)) – точки перегиба.
Теорема 1. (Достаточные условия выпуклости и вогнутости графика функции).
Если во всех точках интервала (a, b) вторая производная функции f (x) отрицательна, т.е. f''(x) < 0, то кривая y = f (x) на этом интервале выпукла.
Если во всех точках интервала (a, b): f ′′(x) > 0, то кривая y = f (x) на этом интервале вогнута.
Доказательство. 1) Пусть f ′′(x) < 0 для x (a, b). Возь-
мем на интервале (a, b) произвольную точку x0 и проведем ка-
сательную M0K к кривой y = f (x) в точке M0(x0, f (x0)) (см. рис. 2.13).
Покажем, что все точки кривой y = f (x) лежат ниже точек касательной M0K (за исключением общей точки M0), т.е. при одном и том же значении x ордината y = f (x) кривой меньше ординаты касательной:
y |
кас |
= f(x ) + f ′(x |
)(x – x ) |
|
|
0 |
0 |
0 |
|
Покажем, что y – yкас< 0. Действительно,
= f (x) – f (x0) – f ′(x0)(x – x0).
Применим к разности f (x) – f (x0) теорему Лагранжа: f (x) – f (x0) = f ′(с)(x – x0),
где c лежит между x и x0, тогда
y – yкас = f ′(с)(x – x0) – f ′(x0)(x – x0) = ( f ′(c) – f ′(x0))(x – x0).
К разности f'(c) – f'(x0) опять применим теорему Лагранжа:
79
f ′(c) – f ′(x0) = f ′′(c1)(c – x0),
где c1 лежит между x0 и c, тогда
y – yкас = f ′′(c1)(c – x0)(x – x0).
Определим знак разности y – yкас. По условию f ′′(c1) < 0.
Покажем, что (c – x0)(x – x0) > 0. Действительно, если x > x0, то c > x0 (так как c лежит между x и x0), следовательно, в этом
случае (c – x0)(x |
– x0) > 0. Если x < x0, то c < x0, то опять |
(c – x0)(x – x0) > 0. |
Значит, y – yкас< 0, т.е. y < yкас. |
Вторая часть теоремы доказывается аналогично.
Теорема 2 (достаточное условие точки перегиба)
Пусть кривая является графиком функции y = f (x). Если f ′′(x0) = 0 или f ′′(x0) не существует и при переходе через x0
вторая производная f ′′(x) меняет свой знак, то точка M0(x0, f (x0)) этой кривой является точкой перегиба.
Доказательство. Пусть для x < x0: f ′′(x) < 0, а для x > x0: f ′′(x) > 0, тогда слева от точки M0(x0, f (x0)) график функ-
ции y = f (x) выпуклый, а справа от M0 – вогнутый, т.е. M0 – точка перегиба.
2.14. Асимптоты
При исследовании функции часто приходится устанавливать вид ее графика (а, значит, и характер функции) при неограниченном удалении точки графика от начала координат (при стремлении переменной точки в бесконечность). При этом важным случаем является тот, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой.
Асимптотой графика функции y = f (x) называется такая прямая, что расстояние от переменной точки M на графике до этой прямой стремится к нулю при удалении точки M в беско-
нечность (рис. 2.14, 2.15).
80
