
2619
.pdflim(x −π)tg |
|
x |
= lim |
x −π |
|
|
|
= lim |
|
|
|
|
|
1 |
|
|
|
|
|
|
= −2 |
|
|
|
|
||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
x→π |
|
|
|
x→π |
|
ctg |
x |
|
|
|
|
|
x→π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
− |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2 |
x |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г) При x → ∞ имеем неопределенность вида 0 ∞ . При- |
|||||||||||||||||||||||||||||||||||||||||||
водим эту неопределенность к виду |
|
0 |
|
|
и пользуемся правилом |
||||||||||||||||||||||||||||||||||||||
0 |
|
||||||||||||||||||||||||||||||||||||||||||
Лопиталя: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
sin |
|
|
|
= lim |
|
|
cos |
|
|
|
|
1 |
=1. |
|||||||||||||||||||||||||
lim x sin |
= lim |
x |
|
|
x2 |
x |
= lim cos |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
x→∞ |
x |
|
x→∞ |
1 |
|
|
|
|
|
x→∞ |
|
1 |
|
|
|
|
|
|
|
|
|
|
x→∞ |
x |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
7.3. Найти пределы: a) |
lim(tgx)tg 2 x ; 6) lim(ln x) |
x |
; |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→ 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
в) lim x x |
; |
r) |
lim(x + 2x ) |
x |
; |
д) |
|
|
lim(1 + sin 2x)ctg 5 x . |
||||||||||||||||||||||||||||||||||
|
|
x→0 |
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
имеем неопределенность 1∞ . |
||||||||||||||||||||||||||||
Решение. a) При x → 4 |
|||||||||||||||||||||||||||||||||||||||||||
Прологарифмируем данную функцию y=(tgx)tg2x; |
|||||||||||||||||||||||||||||||||||||||||||
ln y = tg2x ln tgx , |
тогда |
lim ln y = lim tg2x ln tgx , т. e. по- |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→π |
|
|
|
|
|
|
|
x→π |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||||||||
лучим неопределенность вида ∞ 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Представим эту неопределенность в виде неопределен- |
|||||||||||||||||||||||||||||||||||||||||||
ности |
0 |
и применим правило Лопиталя |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim ln y = lim |
ln tgx |
|
= −lim |
sin 2 |
2x |
= −1. |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
tg2x |
|
sin 2x |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
x→ 4 |
|
|
|
x→ |
4 |
|
|
|
|
x→ 4 |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
π |
|
|
|
|
π |
|
1 |
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
181
Так |
как |
lim ln y = −1 , |
то |
lim y = e−1 |
= |
|
|
1 |
|
или |
|||||||||||||||||||||||||||||||
e |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x→π |
|
|
|
|
|
|
|
|
x→π |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
lim(tgx)tg 2 x = |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x→π |
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6) Неопределенность вида ∞0 . Прологарифмируем дан- |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ную функцию y = (ln x) |
x |
|
|
ln y = |
ln ln x |
и сведем неопреде- |
|||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ленность к виду |
∞ : |
lim ln y = lim ln ln x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∞ |
x→∞ |
|
|
|
|
x→∞ |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Применим правило Лопиталя |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
ln ln x |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
lim |
|
= lim |
|
x |
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x→∞ |
x |
x→∞ ln x |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||
Так как lim ln y = 0 , то lim y =1 или |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
lim(ln x) |
x |
=1. |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
в) Неопределенность вида 00. Прологарифмируем функ- |
|||||||||||||||||||||||||||||||||||||||||
цию y=xx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ : |
||
. |
Представим |
|
неопределенность |
|
|
в |
|
|
виде |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
||
|
|
ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln x |
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||
lim ln y = lim |
|
. Применим правило lim |
= lim |
|
|
|
x |
= 0 . |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
x→0 |
x→0 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
1 |
|
|
x→0 |
1 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x2 |
|
|
|
|
||||||||||||
Отсюда lim ln y = 0 , lim y =1 . |
Итак lim x x |
=1. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
x→0 |
|
|
x→0 |
|
|
|
|
x |
→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
г) Неопределенность вида ∞0 . Положим |
y = (x + 2x ) |
x |
и |
||||||||||||||||||||||||||||||||||||||
прологарифмируем: ln y = |
|
1 |
ln(x + 2x ) . Применяя правило Ло- |
||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
питаля, получим
182
|
lim ln y = lim |
ln(x + 2x ) |
= lim |
1 |
+ 2x ln 2 |
= |
|
|||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
x + 2x |
|
|
||||||||||||||||||
|
x→∞ |
2x |
x→∞ |
|
|
|
|
|
2x |
|
x→∞ |
|
|
|
|
|
|
|
||||||||||||||
|
= lim |
|
ln 2 2 |
= lim |
ln3 2 |
|
= ln 2 , |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
2x |
ln2 2 |
|
|
|
|
||||||||||||||||||||
|
|
|
x→∞ 1 + 2x ln 2 |
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
откуда lim y |
= 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
д) Неопределенность вида 1∞ . Прологарифмируем функ- |
||||||||||||||||||||||||||||||||
цию y = (1 +sin 2x)ctg 5x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
lim ln y = lim ctg5x ln(1 +sin 2x) |
|
и приведем неопределен- |
||||||||||||||||||||||||||||||
x→0 |
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ность к виду |
|
0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
|
ln(1 + sin 2x) |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
lim ln y = lim cos 5x |
. |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
x→0 |
|
|
x→0 |
|
|
|
|
|
|
sin 5x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пользуясь теоремами о пределах и правилом Лопиталя, |
||||||||||||||||||||||||||||||||
будем иметь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 cos 2x |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
ln(1 + sin 2x) |
|
|
|
|
|
|
|
|
|
|
||||||||||||
lim ln y = lim cos 5x |
= lim 1 + sin 2x |
= |
||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
x→0 |
|
|
|
x→0 |
|
|
|
|
|
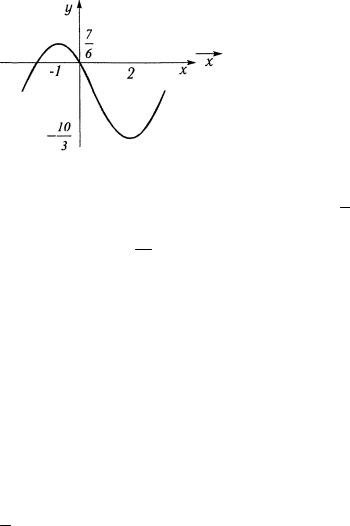
sin 5x |
|
|
|
x→0 |
|
|
|
|
5cos 5x |
|
|
|
||||||||||
|
= |
2 |
lim |
|
1 |
|
|
= |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
5 x→0 1 + sin 2x |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, |
lim(1 + sin 2x)ctg 5x = e |
5 |
. |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2.8. Возрастание и убывание функций
При исследовании поведения функции у = f(x) в зависимости от изменения независимой переменной х обычно предполагается, что во всей области определения функции независимая переменная изменяется монотонно возрастая, т. е. каждое следующее ее значение больше предыдущего x2 > x1 .
Если при этом последовательные значения функции также возрастают f(x2)>f(x1), то функция называется возрастаю-
183
щей, а если они убывают f(x2)<f(x1), то функция называется
убывающей.
Возрастание и убывание функции характеризуется знаком ее производной: если внутри некоторого промежутка у′ > 0 , то функция возрастает, а если y′ < 0 , то в этом проме-
жутке функция убывает.
При практическом исследовании функции на возрастание и убывание находят производную и приравнивают ее к нулю. Находят корни получившегося уравнения, а также точки, в которых производная не существует. Все эти точки, вместе с возможными точками разрыва функции, разбивают область существования функции на ряд промежутков, на каждом из которых вопрос о возрастании или убывании функции определяется знаком производной.
8.1. Определить промежутки монотонности функций:
2 |
|
|
|
|
|
y = |
x2 |
|
а) y =3x -1; б) y=loga(x-1); а < 1; |
в) |
|
; |
|||||
x −1 |
||||||||
г) у = (х + 1)3(x-3); д) y = x2 |
|
x |
|
. |
|
|
|
|
|
|
|
|
|
|
|||
Решение. а) Функция определена |
для всех значений х, |
|||||||
т. е. область ее существования (− ∞;+∞). |
Находим производ- |
|||||||
ную у = 3x2. Очевидно, что при любом х |
y′ > 0 , следовательно, |
|||||||
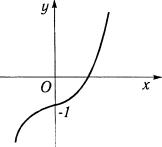
функция возрастает на всем промежутке (рис. 2.17).
Рис. 2.17
184

б) Функция существует для всех х>1, т. е. область ее су-
ществования (1, ∞). Находим производную y′ = 1 . По- (x −1) ln a
скольку a < 1 , то lnа < 0 и у' для всех х > 1 меньше нуля. Следовательно, данная функция на промежутке (1, ∞)
убывает (рис. 2.18).
Рис. 2.18
в) Функция определена для всех х кроме x=1, где она
терпит разрыв. Находим производную y′ = x(x − 2) и прирав- (x −1)2
ниваем ее к нулю x(x − 2) = 0 . Это уравнение имеет два корня:
x1=0 , x2=2.
Учитывая точку разрыва х = 1, разбиваем числовую ось на промежутки (рис. 2.19) и определяем знак производной на каждом из них. Следовательно, функция возрастает на проме-
жутках (- ∞,0) и (2, ∞) и убывает - (0,1) и (1,2). На рис. 2.20 по-
казан график функции.
Рис. 2.19
185
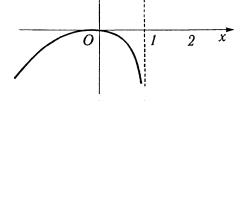
Рис. 2.20
г) Функция определена на всей числовой оси х. Находим производную y′ = 3(x +1)2 (x −3) + (x +1)3 = 4(x +1)2 (x − 2) . Из уравнения (х + 1)2(х -2) = 0 определяем корни производной x1,2 = −1 и x3 = 2. Корни уравнения определяют три промежут-
ка ] −∞, −1]; ] −1, 2] и ]2, ∞[ . Из выражения производной вид-
но, что при переходе через корень x1,2 = -1 производная не меняет знака. При x < −1 и при -1 < х < 2 имеем: y′ < 0 , следова-
тельно, функция убывает. При х > 2 производная y′ > 0 , сле-
довательно функция возрастает.
д) Функция y определена на всей числовой оси. Находим ее производную
|
2 |
|
при |
x > 0; |
|
3x |
|
|
|||
y′ = |
|
|
|
|
|
|
|
2 |
|
|
|
−3x |
при |
x < 0. |
|||
|
|||||
Отсюда следует, что функция при х < 0 убывает, так как y′ < 0 при любом значении х, а при x > 0 возрастает, так как
y′>0.
График этой четной функции показан на рис. 2.21. 186
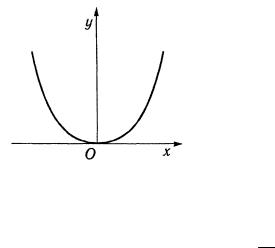
Рис.2.21.
8.2. Доказать справедливость неравенств: а) tgx > x3 + x
3
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
x > ln(1 + x) при х > 0; в) |
|
|
|
x3 |
|
|||||||||
при 0 < x < |
|
|
; б) |
x − |
|
|
|
|
< sin x < x |
||||||||||||||||||||||
2 |
|
3 |
|
||||||||||||||||||||||||||||
при х > 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
Решение. |
а) |
Найдем |
|
|
производную |
|
|
|
функции |
||||||||||||||||||
y = tgx − |
|
x |
3 |
|
+ x |
|
для |
|
указанных |
значений |
х: |
||||||||||||||||||||
3 |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
у′ |
= |
|
|
|
− x |
2 |
−1 |
= tg |
2 |
x − x |
2 |
. |
|
|
|
|
|
|
|
|
|
||||||||||
cos2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
Поскольку tg2x - x2 > 0, так как tg2x > x2, |
|
|
tgx > x, то |
||||||||||||||||||||||||
у |
′ |
> 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|||||
|
и |
функция возрастает, |
откуда tgx − 3 |
|
− x > 0 |
или |
|||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
tgx > |
|
x3 |
|
|
+ x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
y = x − ln(1 + x) : |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
б) |
|
|
|
Найдем |
производную |
функции |
|||||||||||||||||||||
|
′ |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y |
=1 −1 + x = x +1 . При x=0 функция имеет минимум, а при |
||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
187 |
|
|
|
|
|
|
|
|
|
|
x > 0, |
y′ > 0 |
и |
функция |
|
возрастает. |
|
Следовательно, |
||||||||||||
x − ln(1 + x) > 0 , откуда x > ln(1 + x) . |
|
|
|
|
|
|
|
|
|
||||||||||
в) Рассмотрим систему неравенств |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − |
x |
< sin x, |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
sin x < x. |
|
|
|
|
|
|
|
|
|
|||||
Введем |
функции f (x) = x − |
x3 |
−sin x, |
ϕ(x) = sin x − x и |
|||||||||||||||
3 |
|
||||||||||||||||||
|
|
|
|
|
′ |
|
|
|
|
2 |
|
|
|
′ |
|
|
|||
найдем их производные |
=1 − x |
|
|
|
|
|
|||||||||||||
f (x) |
|
− cos x, ϕ (x) = cos x −1. |
|||||||||||||||||
При |
x > 0, f |
′ |
|
|
как |
1 − x |
2 |
|
< cos x , |
и |
|
′ |
или |
||||||
(x) < 0 , так |
|
|
ϕ (x) < 0 |
||||||||||||||||
равна |
нулю |
для |
значений |
x = 2πκ (κ = 0,1,2...) , так |
как |
||||||||||||||
cosx<1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функции убывающие, следовательно x − |
|
x3 |
−sin x < 0, и |
||||||||||||||||
|
3 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x − x < 0 , откуда x − |
x3 |
< sin x < x . |
|
|
|
|
|
|
|||||||||||
3 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.9. Максимум и минимум функции
10. Значение функции y=f(x) в точке х0 называется максимальным (минимальным), если оно является наибольшим (наименьшим) по сравнению с ее значениями во всех достаточно близких точках слева и справа от х0.
Максимум и минимум функции называется экстремумом
функции. Значения аргумента, при которых функция имеет экстремум, называются критическими значениями или критическими точками.
Чтобы найти экстремальные значения функции, надо найти ее производную f ′(x) и, приравняв ее к нулю, решить
уравнение f ′(x) = 0 . Корни этого уравнения, а также точки, производная в которых не существует, являются критическими
188
точками, т. е. значениями аргумента, при которых может быть экстремум.
Если знак производной при переходе через точку x0 меняется с плюса на минус, то x0 есть точка максимума; если знак производной меняется с минуса на плюс, то х0 есть точка минимума; если знак не меняется, то в точке x0 экстремума нет.
Иногда проще исследовать критическую точку по знаку второй производной.
Если в критической точке, где первая производная равна нулю, f ′′(x) <0, x0 есть точка минимума; если f ′′(x) < 0, то x0
есть точка максимума; если f ′′(x0 ) = 0, то такую точку иссле-
дуют по первой производной.
20. Если функция задана неявно F(x,y) = 0, то для того
|
y |
′ |
|
Fx′(x, y) |
|
|
|
чтобы |
= − Fy′(x, y) |
= 0 , |
должно выполняться равенство |
||||
|
|||||||
Fx′(x, y) = 0 . Здесь Fx′ |
и Fy′ |
производные от функции F по x и |
|||||
y, найденные в предположении, что у и х не зависят от х и у, соответственно.
Решая совместно F(x,y) = 0 и F ′(x,у) = 0, находим критические точки. Экстремум функции в критических точках на-
ходят по знаку второй производной y′′xx = − |
Fxx′′ |
. Если в крити- |
||||||
Fx′ |
||||||||
|
|
′′ |
|
′′ |
|
|||
|
|
|
|
> 0 , то |
||||
ческой точке yxx < |
0 , то это точка максимума; если yxx |
|||||||
это точка минимума. |
|
|
|
|||||
9.1. Исследовать на экстремум функции: |
|
|
||||||
а) y = |
x3 |
− |
x2 |
− 2x ; 6) y = x(x − 2)3 . |
|
|
|
|
|
|
|
|
|
||||
3 |
2 |
|
|
|
|
|||
Решение. а) Находим производную y′ = x2 − x − 2 . При-
равниваем ее к нулю x2 − x − 2 = 0 . Корни этого уравнения x1=-1 ; x2=2 являются критическими точками.
189
Представим |
производную в следующем виде |
y′ = (x +1)(x − 2) |
и рассмотрим методом интервалов, как меня- |
ется знак при переходе через критические точки (рис. 2.22).
Рис. 2.22
При переходе через точку x1 = -1 производная меняет знак с плюса на минус, а при переходе через x2 = 2 с минуса на плюс. Значит, при x1= -1 функция имеет максимум, а при x2 = 2 функция имеет минимум.
Находим экстремальные значения функции: f (−1) = 76 -
максимум функции; f (2) = −103 минимум функции. График функции показан на рис. 2.23.
Рис. 2.23
б) Находим производную y′ = 2(x − 2)2 (2x −1) и приравниваем ее к нулю (x − 2)2 (2x −1) = 0 . Корни этого уравнения
x1= 2, x2 = 12 являются критическими точками.
При переходе через точку x1 =2 производная знака не меняет, поскольку данный множитель в квадрате, а при переходе
190
