
2619
.pdfy = f (x + x) − f (x) = (2,12 + 3 2,1 +1) − (22 +3 2 +1) = =11,71 −11 = 0,71.
Следовательно, приращение ординаты касательной равно
0,7, |
а приращение функции 0,71. Так как |
у = dy + α х, то |
||
α х = 0,71 - 0,7 = 0,01. |
|
|
||
4.6. |
Найти |
дифференциал и |
приращение функции |
|
y = x3 − 2x при |
х = 2 и х = 0,1. |
Найти |
абсолютную и |
|
относительную погрешности при замене приращения функции её дифференциалом.
Решение. Имеем: dy = (3x2 − 2)dx ,
y = ((x + x)3 − 2(x + x)) − (x3 − 2x) = (3x2 + 3x x + x2 − 2) x
При x = 2 и x = |
0,l |
получим: dy = (3 22 − 2) 0,1 =1; |
|||||||
y = (3 22 + 3 2 |
0,1 |
+ 0,12 − 2) 0,1 =1,061. |
|||||||
Абсолютная погрешность |
= | у - dy| = 0,061, а oтноси- |
||||||||
тельная погрешность δ = |
|
|
|
|
100% = |
0,061 |
100% ≈ 6% . |
||
|
y |
|
|
|
|||||
|
|
|
|
|
1,061 |
|
|||
4.7. При измерении сторона куба х оказалась равной 4см, причём максимально возможная при этом погрешность измерения х находится в пределах ± 0,01см. Определить абсолютную и относительную погрешности при вычислении объёма куба.
Решение. Объём куба равен V = x3 = 64 см3. Возможная
неточность |
измерения |
| |
х | = 0,01. Отсюда абсолютная |
||||||||||
погрешность |
|
V |
|
≈ |
|
|
|
dV |
|
|
= 3x2dx = 3 42 0,01 = 0,48. Относи- |
||
|
|
|
|
||||||||||
тельная погрешность |
|
dV |
|
|
0,48 |
100% = 0,75% . |
|||||||
|
|
|
= |
||||||||||
V |
|
64 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
161
2.5. Приложения производной к задачам геометрии и физики
10. Уравнение касательной и нормали к кривой. Значение производной f ′(x) в некоторой точке x = x0 геометрически
представляет угловой коэффициент касательной к графику функции y = f (x) в точке x = x0 .
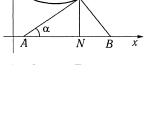
Из геометрического смысла производной следует, что угловой коэффициент касательной к кривой y = f (x) (рис. 2.8) в точке M (x0 , y0 ) M y равен значению производной в этой
точке, т. е. k = tgα = f ′(x0 ) . Поэтому, если в уравнение пучка
прямых, проходящих через точку М, подставить угловой коэффициент касательной, то уравнение касательной к кривой в данной точке примет вид y − y0 = f ′(x)(x − x0 ).
Нормалью к кривой в точке M (x0 , y0 ) называется пря-
мая, проходящая через точку M перпендикулярно касательной и кривой в этой точке. В силу условия перпендикулярности
двух |
прямых |
|
k1 |
= − |
1 |
, уравнение нормали имеет вид |
|||
|
|
||||||||
|
|
|
|
|
|
k2 |
|
||
y − y0 |
= − |
1 |
|
(x − x0 ) , если |
f ′(x0 ) ≠ 0 . |
||||
f ′(x0 ) |
|||||||||
|
|
|
|
|
|
|
|||
Отрезки |
AM = y0ctgα , |
BN = y0tgα называются, соответ- |
|||||||
ственно подкасательной и поднормалью, а длины отрезков АМ и ВМ – длинами касательной и нормали.
Рис. 2.8
162
20. Углом между кривыми y = f1 (x) и y = f2 (x) в точке их пересечения M (x0 , y0 ) называется угол между касательны-
ми к этим кривым в точке M0 . Этот угол находится по известной формуле аналитической геометрии
|
|
|
′ |
′ |
|
|
tgϕ = |
|
f2 |
(x0 ) − f1 |
(x0 ) |
||
1 |
|
′ |
′ |
(x0 ) |
||
|
+ f1 (x0 ) f2 |
|||||
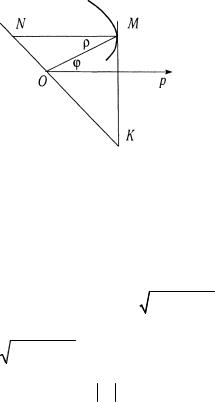
30. Отрезки, связанные с касательной и нормалью, в полярной системе координат. Пусть кривая задана в полярных координатах уравнениемρ = ρ(ϕ) (рис. 2.9), тогда угол, обра-
зованный касательной МК и полярным радиусом ρ = ОМ, оп-
ределяется по формуле tgα = ρ .
ρϕ′
Рис. 2.9
Касательная МК и нормаль MN в точке М вместе с полярным радиусом ОМ точки касания и перпендикуляром к полярному радиусу, проведённому через полюс О, определяют
следующие четыре отрезка: |
|
MK = |
|
|
ρ |
|
2 |
′ 2 |
- отрезок ка- |
||||||||
|
|
|
|
|
|
|
ρ |
|
+(ρ ) |
||||||||
|
|
|
ρ |
|
|
|
|
||||||||||
|
|
|
|
||||||||||||||
сательной; MN = ρ |
2 |
′ |
2 |
|
|
|
|
|
|
|
|
|
|
OK = |
ρ2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
+(ρ ) |
|
- отрезок |
нормали; |
ρ′ |
- |
|||||||||||
полярная подкасательная; ON = ρ′ -полярная поднормаль.
163

40. Средняя скорость движения точки за промежуток времени t определяется отношением приращения пути S ко времени. Чем меньше t , тем точнее выражается скорость через среднюю скорость. Скорость движения точки в момент
времени t определяется пределом, к |
которому стремится |
|||
средняя скорость при t → 0 , т. е. v = lim |
S |
= |
dS |
. |
t |
|
|||
t→0 |
|
dt |
||
При движении точки по окружности угловой скоростью вращения ω в момент времени t называют предел отношения
ϕt , когда t стремится к нулю, т. е.
ω = lim |
ϕ |
= |
dϕ |
= ϕ . |
|
t |
dt |
||||
t→0 |
|
|
Таким образом, угловая скорость в данный момент равна производной от угла поворота ϕ по времени.
Ускорение точки ω , движущейся по прямой, есть первая производная от скорости по времени ω = dvdt или вторая произ-
водная от пути S по времени ω = |
d 2 S |
. |
|
dt2 |
|||
|
|
Угловое ускорение точки есть первая производная от уг-
ловой скорости ε = ddtω или вторая производная от угла пово-
рота по времени ε = d 2ϕ . dt 2
50. Сила тока определяется как предел отношения dqdt
при t → 0 , где q положительный электрический заряд, переносимый через сечение цепи за время t , т.е.
I = lim |
q |
= |
dq |
. |
t |
|
|||
t→0 |
|
dt |
||
164
Таким образом, сила тока в данный момент времени равна производной от количества протёкшего электричества по времени.
60. Химическое истолкование производной. Пусть Q(t) - концентрация вещества, получаемого в ходе химической реак-
ции в момент времени t . Тогда С′(t0 ) = lim |
Q(t0 ) - скорость |
||||||||||||||||||||||||||
реакции в момент t0 . |
|
|
|
|
|
|
t→0 |
|
|
t |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
5.1. Написать уравнение касательной и нормали к кри- |
|||||||||||||||||||||||||
вой y |
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
= |
|
|
|
|
|
в точке M 1, |
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
x |
|
+1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2x |
|
|||
|
|
Решение. |
|
|
|
|
|
|
|
|
y |
′ |
|
|
|
|
|
|
|||||||||
|
|
|
Находим производную |
= − (x2 |
+1)2 |
и вы- |
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
1 |
числяем частное значение производной при x =1: y (1) = − 2 . |
|||||||||||||||||||||||||||
|
1 |
Таким |
1 |
|
|
образом, |
уравнение |
касательной |
будет |
||||||||||||||||||
y − |
|
= − |
|
|
|
|
|
|
или x +2 y −2 = 0 . |
|
|
|
|
|
|
|
|
|
|||||||||
2 |
|
2(x −1) |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
Уравнение нормали к кривой в точке |
|
M 1, |
|
|
имеет вид |
||||||||||||||||||||
|
|
|
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y − |
1 |
|
= 2(x −1) или |
4x −2 y −3 = 0 . |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.2. Написать уравнение касательной и нормали к эл- |
|||||||||||||||||||||||||
|
|
|
|
x2 |
|
|
y 2 |
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
||||
липсу |
|
|
|
+ |
|
|
|
=1 в точке |
M |
|
, 4 . |
|
|
|
|
|
|
|
|
|
|||||||
9 |
25 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Решение. |
|
|
|
Находим |
|
|
|
|
|
производную |
|||||||||||||||
2x |
|
2 yy′ |
|
|
|
|
|
′ |
|
25x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
9 + 25 = 0, y |
= − 9 y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
165
Вычисляем частное значение производной в точке M
|
9 |
|
− 25 9 1 |
|
5 |
|
|||||
y′ |
|
|
= |
|
|
|
|
= − |
|
. Отсюда уравнение касательной |
|
5 |
9 5 4 |
4 |
|||||||||
|
|
|
|
|
|||||||
y − 4 = − |
5 |
(x − |
9 |
) |
или 5x + 4 y −25 = 0 . |
|
|
|
|
|
|
|
4 |
5 |
|
4 |
|
9 |
|
||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
Уравнение |
нормали имеет вид |
y −4 = − |
|
x − |
|
|
или |
|||||
5 |
5 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
20x −25y +64 = 0 .
5.3. На кривой y = 3x2 − 4x +1 найти точку, в которой касательная параллельна прямой y = 2x .
Решение. Пусть искомая точка касания есть M (x0 , y0 ) .
Находим угловой коэффициент касательной в точке касания k = y′(x0 ) = 6x0 − 4 .
Поскольку касательная и прямая параллельны, то их угловые коэффициенты равны 6x0 −4 = 2 , откуда x0 =1.
Подставляя найденное значение абсциссы искомой точки в уравнение кривой, находим её ординату y0=3·12-4·1+1=0.
Итак, точка М имеет координаты (1,0).
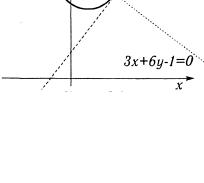
5.4. Найти точку линии у = х2-2х-5, в которой касательная перпендикулярна прямой Зх + 6y -1 = 0, составить уравнение этой касательной. Сделать чертёж.
Решение. Пусть искомая точка есть M(x0 , y0). Находим
угловой коэффициент касательной y′(x0 ) = 2x0 |
− 2 . Угловой |
|||||
коэффициент прямой k1 = − |
1 |
. |
|
|
|
|
|
|
|
|
|||
2 |
|
|
1 |
|
||
Из условия перпендикулярности прямых |
k1 = − |
, где |
||||
|
||||||
|
|
|
|
k2 |
||
k2 - угловой коэффициент касательной, находим абсциссу ис-
комой точки |
− |
1 |
= − |
1 |
, x0 = 2. Ординату точки М нахо- |
|
2 |
2x0 − 2 |
|||||
|
|
|
|
166
дим из уравнения линии у0= x02 − 2x0 + 5 = 5. Уравнение каса-
тельной будет y - 5 = 2(x-2) или 2х - у + 1 = 0.
Чтобы построить график параболы, преобразуем её уравнение y = x2 - 2x+5=(x-1)2+4, т. е. вершина параболы сдвинута на единицу вправо и на четыре единицы поднята вверх (рис.2.10). Уравнения касательной и прямой, перпендикулярной касательной, показаны на рисунке.
Рис. 2.10
5.5. Найти длину подкасательной, поднормали и нормали кривой y2=x3 в точке x0=1.
Решение. Данная кривая представляет полукубическую параболу.
Поскольку касательная и нормаль проходят через точку x0=1, y0=1,то рассмотрим только одну ветвь кривой (рис. 2.11)
.AN-подкасательная; BN-поднормаль. y
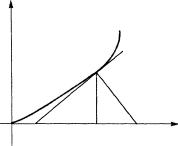 x Рис. 2.11
x Рис. 2.11
167
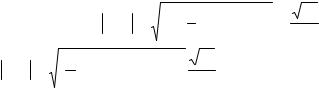
Найдём угловой коэффициент касательной в точке М:
2 yy |
′ |
= 3x |
2 |
, y |
′ |
= |
|
3 x2 |
′ |
= |
3 |
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
2 y |
; y (1) = k1 |
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М(1,1) будет |
||||
|
|
Угловой |
|
коэффициент |
нормали в точке |
|||||||||||||||||
k2 = − |
1 |
|
|
= − |
2 |
. Уравнение касательной y-1 = |
3 |
|
(x-1); нормали |
|||||||||||||
k1 |
3 |
2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
у -1= − |
|
2 |
|
|
(x-1). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найдём координаты точек A и B. Поскольку точки лежат на оси Ох, то y = 0 и из уравнений касательной и нормали име-
|
1 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ем A |
|
,0 , B |
|
|
|
,0 |
. Длина |
подкасательной |
|
AN |
=1 − |
|
= |
|
; |
|||||||||
3 |
2 |
|
3 |
3 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
поднормали |
|
BN |
|
= |
5 |
−1 = |
3 |
. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
AM = (1 − 1)2 |
+ (1 − 0)2 = |
13 |
; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Длина |
|
касательной |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
длина нормали |
|
|
BM = |
( 5 −1)2 |
+ (1 − 0)2 = |
13 . |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
5.6. Под каким углом |
пересекаются |
кривые у =sin x и |
||||||||||||||||||||||
y = cos x, |
x [0;π]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Решение. Совместно решив уравнения кривых (рис. |
||||||||||||||||||||||||
2.12), |
|
|
находим |
|
абсциссу |
точки |
их |
|
пересечения: |
|||||||||||||||
sin x − cos x = 0, tgx =1, |
x0 = |
π |
. Продифференцируем уравне- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
ния кривых y′ = cos x и y = −sin x . Найдем угловые коэффициенты касательных к кривым в точке их пересечения т. е.
168

значения |
производных |
при |
x0 = π : |
f1′= (x0 ) = |
2 |
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
2 |
|
f2′(x0 ) = − |
2 . Отсюда по формуле (4) пункта 3.4 имеем: |
|
|
||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
2 |
− |
2 |
|
|
|
|
|
|
||||
tgϕ = |
|
2 |
2 |
|
= −2 |
2 , |
ϕ = −arctg2 |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
||||||||
|
1 − |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
||
|
2 |
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Рис. 2.12 |
|
|
|||
|
5.7. Под каким углом кривая |
y = ln( 3x −1) пересекает |
|||||
ось x? |
|
|
|
|
|
|
|
|
Решение. Находим точку пересечения кривой с осью Ох. |
||||||
|
Полагая у=0, получим: |
|
ln( |
3x −1) = 0 , |
3x −1 =1, |
||
x = |
2 |
= 2 3 . |
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
Находим производную y |
′ |
= |
3 |
|
||
|
3x |
−1 и угловой коэффици- |
|||||
|
|
||||||
ент касательной к кривой в точке x0 = |
2 3 . |
|
|||||
|
|
|
|
|
|
3 |
|
169
Поскольку угловой коэффициент оси Ох равен нулю, то по формуле (4) пункта 3.4: tgϕ =  3 . Следовательно, искомый
3 . Следовательно, искомый
угол ϕ = π3
5.8. Найти длины отрезков полярных касательной, нормали, подкасательной и поднормали, а также угол между касательной и полярным радиусом точки касания у спирали Архимеда ρ = aϕ в точке с полярным углом ϕ = 2π .
Решение. |
Представим |
|
|
график |
|
спирали Архимеда |
||||||||||||||||||||||||||||||
(рис.2.13). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Находим производную ρ′ = a , тогда длина полярной ка- |
||||||||||||||||||||||||||||||||||||
сательной равна |
|
|
|
|
|
|
|
|
2πa |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
ρ |
|
2 |
′ |
2 |
|
|
|
|
|
|
2 |
|
2 |
|
|
2 |
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
MK |
= |
|
|
|
|
|
ρ |
|
+ (ρ ) |
|
|
= |
|
|
a |
|
4π |
|
a |
|
+ a |
|
= |
2πa 1 + 4π |
|
; |
|||||||||
|
ρ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
длина полярной нормали |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
MK |
|
= ρ2 + (ρ′)2 = (2πa)2 + a2 = a 1 + 4π 2 ; |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||
длина подкасательной OK = |
|
|
ρ2 |
= |
|
a2 |
4π |
2 |
= 4aπ |
2 |
; |
|
|
|||||||||||||||||||||||
|
|
ρ′ |
|
|
|
a |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
длина поднормали |
|
ON = |
|
ρ′ |
|
= a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Рис.2.13
170
