
2619
.pdfЛевосторонний и правосторонний пределыфункции вточке
Переходим к рассмотрению односторонних пределов функции в точке x0, при которых переменная x «движется» к x0 слева (левосторонний предел) или справа (правосторонний предел). Нам потребуется понятие полуокрестности.
Пусть δ > 0. Интервал (a, x0) называется левой полуокрестностью точки x0, интервал (x0 – δ, x0) – левой δ-
полуокрестностью точки x0. Интервалы (x0, b), (x0, x0 + δ) называются, соответственно, правой полуокрестностью и правой δ-полуокрестностью точки x0.
Пусть f (x0) определена в левой полуокрестности точки x0.
Число b называется левосторонним пределом функции
f(x) в точке x0 (обозначение: lim f(x) = b), если для любого
x→x0 −0
ε > 0 найдется δ > 0, такое, что для всех значений x, принадлежащих левой δ-полуокрестности (x0 – δ, x0), выполняется неравенство: |f(x) – b| < ε.
Символически lim f(x) = b означает:
x→x0 −0
ε > 0 δ > 0 x (x0 – δ < x < x0 → | f(x) – b | < ε).
Аналогично, число b называется правосторонним пределом
функции f(x) в точке x0 (обозначение: lim f(x) = b), если
x→x0 +0
для любого ε > 0 найдется δ > 0, такое, что для всех значений x, принадлежащих правой δ-полуокрестности (x0, x0 + δ), выполняется неравенство: | f(x) – b | < ε.
Символически lim f(x) = b означает:
x→x0 +0
ε > 0 δ > 0 x (x0 < x < x0 + δ → |f(x) – b| < ε).
Пример 3. Функция f (x) задана равенством (рис. 1.7):
2x −1, |
если |
x <1 |
||
|
|
2, |
если |
x =1 . |
f(x) = |
|
|||
|
4 |
− x, |
если |
x >1 |
|
||||
21
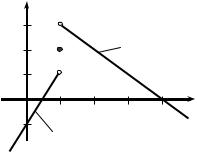
Найти lim f(x) и |
lim f(x). |
|
x→1−0 |
x→1+0 |
|
Решение. Покажем, что lim f(x) = 1, а |
lim f(x) = 3. |
|
|
x→1−0 |
x→1+0 |
Рассмотрим значения x < 1, тогда f (x) = 2x – 1 и |f(x) – 1|= =|2x – 1 – 1| = 2|x – 1|. Зафиксируем малое ε > 0. Подсчитаем: | f(x) – 1| < ε
2 |x – 1| < ε |x – 1| < ε2 . Так как x < 1, то | f (x) – 1| < ε, если
y
3
2
1
0
−1
y = f ( x )
1 2 3 4 y = f ( x )
Рис. 1.7
1 – ε2 < x < 1, следовательно,
δ = ε2 . Итак, если
1 – |
ε < x < 1, то | f(x) – 1| < ε, |
x т.е. |
2 |
lim f(x) = 1. |
|
|
x→1−0 |
Рассмотрим значения x > 1, тогда f (x) = 4 – x. Зафиксируем
ε > 0, | f(x) – 3| = |2 – x – 3| = |1 – x|. Отсюда | f(x) – 1| < ε |1 – x| < ε,
т.е. | f(x) – 1 | < ε для x (1, 1 + ε). |
|
|
||
Значит, lim |
f (x) = 3. |
|
|
|
x→1+0 |
|
|
|
|
Очевидно, если lim f (x) = b, |
то |
|
||
lim |
x→x0 |
lim |
|
|
f (x) = b и |
f (x) = b. |
|||
x→x0 −0 |
x→x0 +0 |
|
||
Верно и обратное, если |
lim |
f(x) = lim f(x) = b, |
||
|
x→x0 +0 |
|
x→x0 −0 |
|
то |
lim f(x) = b. |
|
|
|
|
x→x0 |
|
|
|
22

Если же правосторонний предел функции в точке x0 не равен
левостороннему пределу функции в точке x0, то lim f (x) = b
x→x0
не существует. Так, в примере 3 функция f (x) не имеет предела
вточке x0.
1.6.Бесконечно-малые функции и их свойства
Функция α (х) называется бесконечно малой (сокращенно: б.м.) при х → а (х →+ ∞, х → –∞) или
(x → x0 – 0, х → x0 + 0), если lim α (х) = 0.
x→a
Используя определение предела фукции при х → +∞, можно перефразировать это определение: функция α (х) называется бесконечно малой при х → +∞, если для любого положительного числа ε найдется такое число x0 что для всех х, больших x0, выполняется неравенство: |α (х)| < ε.
Символически это выглядит так:
ε > 0 x0 x > x0 (|α (х)| < ε).
Аналогично формулируются определения б.м. при x →+∞,
х → x0, и т.д.
Пример 1. Функция α (х) = |
|
1 |
является б.м. при x → +∞ |
||||||||
|
|
||||||||||
|
|
|
|
|
|
x |
|
|
|
||
и x → −∞ (см. разд. 1.4, пример 3). |
|
|
|
||||||||
Пример 2. Покажем, что α (х) = |
1 |
б.м. при |
|
x → +∞. |
|||||||
x2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Действительно, неравенство |
|
1 |
|
|
< ε выполняется для всех х, |
||||||
|
|
|
|||||||||
x2 |
|||||||||||
которые удовлетворяют неравенству x > |
1 , т.е. x |
0 |
= 1 . |
||||||||
|
|
|
|
|
|
|
|
|
ε |
ε |
|
|
|
|
|
|
|
|
|
|
|
||
Рассмотрим некоторые теоремы о б.м. функциях. Теорема 1. Сумма двух бесконечно малых функций
(приx → a ) является б.м. функцией (приx → a ).
23

Пример 3. Функция |
1 |
+ |
|
1 |
|
является б.м. при |
x → +∞, |
|
x |
x2 |
|||||||
|
|
|
|
|
||||
так как каждое слагаемое |
1 |
, |
|
1 |
|
является б.м. при |
x → +∞ |
|
x |
|
x2 |
||||||
|
|
|
|
|
||||
(см. примеры 1, 2).
Для дальнейшего нам потребуется понятие огранчености функции.
Функция f (x) называется ограниченной на некотором множестве М, если существует такое положительное число К, что для всех x М выполняется неравенство:
f (x) ≤ K .
Пример 4. Функция sinx и cosx ограничены на множестве R всех действительных чисел, так как x R( sin x ≤1) и
x R( cos x ≤1) .
Теорема 2. Если существует lim f (x), то функция f (x)
x→a
ограничена при х → а.
Следствие 1. Любая б.м. функция при x → a является ограниченной при x → a .
Теорема 3. Если существует lim f (x) и он отличен от
x→a
нуля, то 1 ограничена при x → a . f (x)
Теорема 4. Произведение б.м. функции (при х → а) на функцию, ограниченную (при х → а) является функцией б.м. (при х → а).
Следствие 2. Произведение функции б.м. при x → a на число является функцией б.м. приx → a .
Следствие 3. Произведение двух б.м. функций есть функция б.м. (при x → a ).
24

1.7. Бесконечно большие функции, их свойства и связь с бесконечно малыми функциями
Функция F(x) называется бесконечно большой (сокращенно б.б.) при x → +∞ (при x → −∞), если для любого положительного числа K существует число x0, такое, что для всех x > x0 выполняется неравенство: |F (x)| > K.
Функция F(x) называется бесконечно большой при x → x0 (при x → x0–0 или x → x0+0 ), если для любого K > 0 существует δ > 0 такое, что для любого
x (x0 – δ, x0 + δ), ( x (x0 – δ, x0) или x (x0, x0 + δ) соответст-
венно) выполняется неравенство |F(x)| > K.
Очевидно, что всякая бесконечно большая функция не
является ограниченной при x → a, а потому lim F (x) не суще-
x→a
ствует.
Если F (x) – б.б. функция при x → a, то говорят, что F (x)
стремится к бесконечности и пишут: lim F (x) = ∞. Если при
x→a
этом F (x) > 0, то пишут: lim F (x) = +∞; если же F(x) < 0, то
x→a
пишут: lim F (x) = −∞.
x→a
Пример 1. F1(x) = x2 является б.б. при x → +∞ и x → −∞, причем F1(x) > 0, поэтому можно записать:
lim |
x2 = + ∞, lim |
|
x2 = + ∞. |
|
x→+∞ |
x→−∞ |
|
||
Пример 2. F2(x) = |
1 |
является б.б. при x → 0, причем |
||
x |
||||
|
|
|
||
|
lim F2(x) = +∞, а lim F2(x) = − ∞. |
|||
|
x→0+0 |
|
x→0−0 |
|
Следующие две теоремы устанавливают связь между бесконечно большими и бесконечно малыми функциями.
Теорема 1. Если функция F(x) является б.б при x → a, то функция F1(x) – б.м. при x → a.
25

1
α(x)
F1(x)
Теорема 2. Если α (x) – б.м. при x → a и α (x) ≠ 0, то
– б.б. при x → a.
Свойство 1. Если F1(x), F2(x) – б.б. при x → a, то функцияF2(x) – б.б. приx → a.
Свойство 2. Если F1(x), F2(x) – б.б. функции при x→a,
причем F1(x) > 0 и F2(x) > 0 (т.е. lim F1(x)=+∞,
x→a
lim F2 (x) = + ∞), то функция F1(x) + F2(x) – б.б. при x → a.
x→a
Свойство 3. Если F(x) – б.б. при x → a и число C ≠ 0, то
CF(x) – б.б. при x → a.
Замечание. Если F1(x) и F2(x) – б.б. функции при x → a, но имеют разные знаки, то F1(x) + F2(x) может быть как б.б.,
так и б.м. при x → a, как иметь предел при x → a, так и не иметь его.
1.8. Основные теоремы о пределах
Теорема 1. Если lim f (x) = b, то f (x) = b +α(x), где α(x) –
x→a
б.м. при x → a.
Доказательство. Пусть lim f (x) = b. Рассмотрим функ-
x→+∞
цию α (x) = f (x) – b и покажем, что α (x) – б.м. при x → +∞ .
Из определения lim f (x) = b имеем, что
x→+∞
ε > 0 x0 x > x0 |f (x) – b| < ε, но так как α (x) = f(x) – b, то
ε > 0 x0 x > x0 |α (x)| < ε , а это означает, что α(x) – б.м. при x → +∞.
Итак, из равенства α (x) = f (x) – b имеем f (x) = b + α (x), где α (x) – б.м. при x → +∞.
26
Теорема 2. Если функцию f(x) можно представить в виде: f (x) = b + α(x), где b – число, α(x) – б.м. функция при x → a, то
lim f (x) = b.
x→a
Доказательство. Пусть f (x) = b + α(x), где α(x) – б.м. при x → +∞, т.е.
ε > 0 x0 x > x0 |α(x)| < ε. |
(*) |
Но α(x) = f (x) – b, поэтому (*) можно записать так: |
|
ε > 0 x0 x > x0 |f (x) – b| < ε, что означает: |
|
lim f (x) = b. |
|
x→+∞ |
|
Следующие теоремы значительно облегчают нахождение пределов.
Теорема 3. Предел суммы (разности) двух функций равен сумме (разности) их пределов, т.е. если
lim f1(x) = b1, |
lim f2(x) = b2, то |
x→a |
x→a |
lim (f1(x) + f2(x)) = b1 + b2, |
lim (f1(x) – f2(x) ) = b1 – b2. |
x→a |
x→a |
Доказательство. На основании теоремы 1: f1(x) = b1 +
+α1(x), f2(x) = b2 + α2(x), где α1(x), α2(x) – б.м. при x → a, тогда f1(x) + f2(x) = (b1 + α1(x)) + (b2 + α2(x)) =
=(b1 + b2) + (α1(x) + α2(x)).
Но α1(x) + α2(x) – б.м. функция при x → a (как сумма двух б.м. функций), поэтому из равенства
f1(x) + f2(x) = (b1 + b2) + (α1(x) + α2(x))
по теореме 2 следует, что
lim (f1(x) + f2(x)) = b1 + b2.
x→a
Аналогично проводится доказательство для разности. Теорема 4. Предел произведения двух функций равен
произведению их пределов, т.е. если |
|
|
lim f1(x) = b1, |
lim f2(x) = b2, то |
lim (f1(x) f2(x)) = b1 b2. |
x→a |
x→a |
x→a |
Доказательство. По теореме 1:
27
f1(x) = b1 + α1(x), f2(x) = b2 + α2(x), где α1(x), α2(x) – б.м.
при x → a, тогда
f1(x) f2(x) = b1 b2 + b1 α2(x) + b2 α1(x) + α1(x) α2(x).
На основании следствий 2, 3, теоремы 1 (разд. 1.6) функ-
ции b1 α2(x), b2 α1(x), α1(x) α2(x) – б.м. при x → a и
α(x) = b1 α2(x) + b2 α1(x) + α1(x) α2(x) – бесконечно малая функция при x → a. Из равенства f1(x) f2(x) = b1b2 + α(x) по тео-
реме 2 следует, что lim (f1(x) f2(x)) = b1b2. |
|
||
|
x→a |
|
|
Следствие 1. Постоянный множитель можно выносить за |
|||
знак предела, т.е. |
|
|
|
lim (С f (x)) = С lim f (x), |
где С – постоянное число. |
||
x→a |
x→a |
|
|
Доказательство. lim С f(x) = lim С lim f(x) = С lim f(x), |
|||
|
x→a |
x→a x→a |
x→a |
так как lim С = С. |
|
|
|
x→a |
|
|
|
Следствие 2. Если n – натуральное число, то |
|
||
|
lim [(f(x))n] = ( lim f(x))n. |
|
|
|
x→a |
x→a |
|
Теорема 5. Предел дроби равен пределу числителя, деленному на предел знаменателя при условии, что предел знаменателя не равен нулю. Иначе, если
|
|
lim f |
1 |
(x) |
|
b1 |
|
lim f1(x) = b1, |
lim f2(x) = b2 и b2 ≠ 0, то |
x→a |
|
= |
. |
||
lim f |
|
(x) |
|
||||
x→a |
x→a |
2 |
|
b |
|||
Доказательство. По теореме 1: |
x→a |
|
2 |
|
|||
|
|
|
|
|
|
||
f1(x) = b1 + α1(x), |
f2(x) = b2 + α2(x), где α1(x), α2(x) – б.м. |
||||||
при x → a, тогда |
|
|
|
|
|
|
|
28

|
|
|
|
f1 (x) |
|
|
b1 +α1 (x) |
|
b1 |
|
|
|
b1 +α1 |
(x) |
|
|
|
|
|
|
||||||||||||
|
|
|
|
= |
= |
+ |
= |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
f2 (x) |
b2 +α2 (x) |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
b2 |
|
|
b2 +α2 (x) |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
= |
|
b1 |
|
+ |
b1b 2 +b 2α1 (x) −b1b 2 −b1α2 (x) |
= |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
b |
2 |
|
|
|
|
|
|
b2 |
+b |
2 |
α |
2 |
(x) |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
= |
b1 |
+ b 2α1 (x) −b1α2 (x) |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
2 |
b2 +b |
2 |
α |
2 |
(x) |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
b2 α1 (x) −b1α2 (x) |
|
|||||||||
|
Обозначим последнюю дробь α(x) = |
|
, |
|||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 +b |
2 |
α |
2 |
(x) |
|
||
|
|
f1 (x) |
|
|
b1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||
тогда |
|
= |
|
|
|
+ α(x). Остается показать, что α(x) – б.м. при |
||||||||||||||||||||||||||
|
f2 (x) |
b2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x → a. Действительно, числитель дроби b2α1(x) – b1α2(x) – б.м. по свойствам бесконечно малых функций, предел
lim (b22 + b2α2(x)) = b22 ≠ 0, на основании теорем 3, 4. Поэтому
x→a
|
|
1 |
|
|
– функция,ограниченная при x → a (по теореме 3 |
|
b2 |
+b |
2 |
α |
2 |
(x) |
|
2 |
|
|
|
|
||
разд. 1.6). Значит, α(x) – б.м. при x → a (по теореме 4 разд. 1.6). Теорема доказана.
Теорема 6. Если |
lim f (x) существует и f (x) ≥ 0 для всех |
||||
|
|
x→a |
|
|
|
x из области определения функции, то lim f (x) ≥ 0. |
|||||
Доказательство. |
Пусть |
x→a |
|
методом от |
|
a = +∞. Докажем |
|||||
противного, предполагая, что |
lim f (x) = b < 0. |
Зафиксируем |
|||
|
|
|
x→∞ |
|
|
ε = – b 2 , ε > 0. |
По определению предела по ε |
найдется x0, |
|||
такое, что x > x0 |
|f(x) – b| < ε, |
отсюда b – ε < f (x) < b + ε. Но |
|||
ε = – b 2 , поэтому x > x0 f(x) < b – b 2 , |
f(x) < b 2 , т.е. |
||||
f(x) < 0, что противоречит условию. Теорема доказана. |
|||||
Теорема 7. Если x (f1(x) ≥ f2(x)) и |
lim f1(x), lim f2(x) |
||||
|
|
|
|
x→a |
x→a |
существуют, то lim f1(x) ≥ lim f2(x). |
|
|
|||
x→a |
x→a |
|
|
|
|
29

Доказательство. Рассмотрим функцию
F(x) = f1(x) – f2(x), тогда x (F (x) ≥ 0) и lim F(x) существует.
x→a
По теореме 6: lim F(x) ≥ 0, |
lim (f1(x) – f2(x)) ≥ 0, |
отсюда |
|
|
x→a |
x→a |
|
lim f1(x) ≥ lim f2(x). Теорема доказана. |
|
||
x→a |
x→a |
|
|
1.9. Сравнение бесконечно малых функций. |
|
||
|
Эквивалентные бесконечно малые функции |
||
Пусть α(x) и β(x) – б.м. |
функции при x → a |
(x→ + ∞, |
|
x → –∞, |
x → x0, ...). Рассмотрим предел их отношения при |
||
x → a. |
|
|
|
1. Если lim α(x) = b и b – конечное число, b ≠ 0, то
x→a β(x)
функции α(x), β(x) называются бесконечно малыми одного по-
рядка малости при x → a.
2. Если lim α(x)
x→a β(x)
лой высшего порядка, чем β(x) при x → a. Очевидно, в этом
случае lim β(x) = ∞.
x→a α(x)
3. Если α(x) – б.м. высшего порядка, чем β(x), и
lim |
α(x) |
= b ≠ 0 (b – конечное число, k N), то α(x) назы- |
|
||
x→a (β(x))k |
|
|
вают бесконечно малой k-го порядка, по сравнению с β(x) при x → a.
4. Если не существует lim α(x) |
(ни конечный, ни |
x→a β(x) |
|
бесконечный), то α(x), β(x) называют несравнимыми б.м. при x → a.
30
