
2619
.pdf
lim |
|
|
(e2 x3 −1)sin 3x |
|
= lim |
2x3 3x |
= −1. |
||||
x → |
0 ln(1 −3x2 )(1 − cos 2x) |
|
|
|
1 |
|
|||||
x→0 |
|
2 |
|
2 |
|
||||||
|
|
|
|
|
|
−3x |
|
|
|
(2x) |
|
|
|
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
б) При x→0 имеем неопределенность вида 00 . Заменяем исходные бесконечно малые эквивалентными и упрощаем
lim ( |
1+sin x −1)arctg3x |
|
1 |
sin x 3x |
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
||||
= lim |
2 |
= lim |
cos x = |
. |
||||||
( |
) |
|
|
|
||||||
x→0 |
x→0 tgx 2x |
x→0 |
4 |
4 |
|
|||||
|
etgx −1 arctg2x |
|
||||||||
1.5. Непрерывность и точки разрыва функции
10. Если |
аргумент |
функции |
получает приращение |
x = x2 − x1 , |
то значение |
функции |
при новом значении |
аргумента равно f(x+ x) = y + y. Отсюда приращение функции y = f(x + x) - f(x), т.е. приращение функции равно разности наращенного значения функции (при наращенном значении аргумента) и начального значения функции. Приращение аргумента может быть не только положительным, но и отрицательным числом.
20. Определение непрерывности функции:
1. Функция у = f(х) непрерывна в точке х = а, если пределы слева и справа равны и равны значению функции в этой точке, т. е.
lim |
f (x) = lim |
f (x) = f (a). |
x→a −0 |
x→a + |
0 |
2. Функция y=f(x) непрерывна в точке х = а, если она определена в этой точке и если бесконечно малому приращению аргумента соответствует бесконечно малое
приращение функции, т.е. lim y = 0 вблизи точки а. Сумма,
x→0
111

разность и произведение конечного числа непрерывных функций есть функция непрерывная.
30. Непрерывная на отрезке [а,b] функция принимает любое промежуточное значение между ее наименьшим т и наибольшим М значением, то есть т ≤ f(x) ≤ М для всех x [a,b]. Отсюда следует, что если в граничных точках отрезка [а,b] функция имеет разные знаки, то внутри отрезка есть, по крайней мере, одно такое значение х = с, при котором функция обращается в ноль. Это свойство непрерывности функций позволяет находить приближенно корни многочленов.
40. Значения аргумента, которые не удовлетворяют условиям непрерывности, называются точками разрыва функции. При этом различают два рода точек разрыва функции.
Если при x→a слева функция имеет конечный предел k1 , а при x→a справа функция имеет конечный предел k2 и
k1 ≠ k2 , то говорят, что функция при x→a имеет разрыв первого рода. Разность k1 − k2 определяет скачок функции в
точке х = а. Значение функции при x=а при этом может быть равно какому угодно числу k 3 .
Если значение функции при х = а равно k1 , то говорят, что функция непрерывна слева; если же k2 , то говорят, что функция непрерывна справа.
Если k1= k2 ≠ k3, то говорят, что функция имеет в точке а
устранимый разрыв.
Если при x→ a справа или слева, предел функции не
существует или равен бесконечности, то есть lim f (x) = ∞ , то
x→a
говорят, что при x= а функция имеет разрыв второго рода.
5.1. Найти приращение функции y=2x3 - 3x + 1, если аргумент x изменился от x1 = 1 до x2 = 2.
Решение. Найдем приращение аргумента
112
x = x2 - x1=2 – 1 = 1. Вычислим исходное значение функции
y(x1) = 2 13 - 3 1 + 1 = 0.
Вычислим новое значение функции
y(x1 + x) = y(1+1) = 2 23 - 3 2 + 1 = 11.
Отсюда приращение функции
|
|
y=y( x1 + |
x ) - y( x1 ) = 11. |
|
|
5.2. Найти приращение функции y=3 x2 -2x+4 и вычислить |
|||||
его при x = 2 и |
x = - 0,1. |
|
|
|
|
Решение. |
Новому |
значению |
аргумента |
x+ x |
|
соответствует новое значение функции |
|
|
|||
|
|
y(x + x) = 3(x + x)2 - 2(x + x) + 4. |
|
||
Приращение функции равно y=y(x + |
x)-y(x)= |
|
|||
=3(x + |
x)2 - 2(x + x) + 4 - 3x2 - 2x – 4 = (3 |
x+6x-2) |
x. При |
||
х =2 и |
x = - 0,1 |
получим y = (-0,3 + 12 - 2)(-0,1) = 0,97 . |
|||
5.3.Найти множество значений х, при которых функция
у= x3 - 2x непрерывна.
Решение. Найдем приращение функции |
|
y=(x + x)3 - 2(x + x) - (x3-2x) = x( x2+3x |
x+3x2-2). |
При любых значениях х приращение |
y→0, если |
только x→0, поэтому функция непрерывна при всех действительных значениях х.
5.4. Доказать непрерывность функции y = |
|
|
1 |
|
|
в точке |
|
||||||||||||||||||||
|
x −1 |
|
|||||||||||||||||||||||||
х = 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Для доказательства найдем приращение |
|||||||||||||||||||||||||||
функции |
|
у |
при |
переходе |
значения аргумента от |
х = 3 к |
|||||||||||||||||||||
х = 3 + х |
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
2 − 2 − x |
|
|
|
|
− x |
|
|
||||
y= |
|
|
− |
|
|
= |
|
|
|
− |
|
= |
= |
|
|
|
. |
||||||||||
3 |
+ |
x −1 |
3 |
−1 |
2 |
+ |
x |
2 |
|
|
2(2 + x) |
||||||||||||||||
|
|
|
|
|
2(2 + |
x) |
|
|
|||||||||||||||||||
Найдем предел приращения функции при |
|
x→0. |
|
|
|
||||||||||||||||||||||
|
|
|
lim |
y = − lim |
|
|
|
x |
|
|
= 0. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2(2 |
+ |
|
x) |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
x→0 |
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Так как предел приращения функции при |
x→0 равен |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
113 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

нулю, то функция при x = 3 непрерывна.
5.5. Найти приближенно хотя бы один корень уравнения
3x3 + 2x2 – x – 1 = 0.
Решение. Найдем точку пресечения графика функции y=3x3 + 2x2 – x – 1 = 0 с осью Ох, то есть точку, в которой у = 0.
Подберем две произвольные точки, в которых функция имеет разные знаки. Пусть х =0, тогда у = - 1 , у < 0. При х = 1,
у = 3 + 2 - 1 - 1 = 3, у > 0 . Значит, |
корень находится между |
|||||||||||||||||||||||||||||||
x= 0 и х = 1 (в силу свойства непрерывности). |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
Определим знак функции в середине промежутка [0,1], т. е. |
|||||||||||||||||||||||||||||
при х =0,5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Находим y=3 0,53+2 0,52-0,5-1=-0,625; y < 0. Значит, корень |
|||||||||||||||||||||||||||||
находится между х = 0,5 и х = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Определим знак функции в середине этого промежутка, |
|||||||||||||||||||||||||||||
т.е. при x = |
3 |
|
|
|
|
|
|
|
|
3 3 |
|
|
|
3 2 |
− |
3 |
−1 = |
41 |
|
|
|
|
|
|||||||||
|
. Находим y = 3 |
|
|
|
|
+ 2 |
|
|
|
|
|
|
. |
|
|
|
||||||||||||||||
4 |
4 |
4 |
4 |
64 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Следовательно, |
|
корень |
находится |
внутри |
промежутка |
||||||||||||||||||||||||
1 , |
3 . Находим знак функции в середине этого промежутка, |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
т.е. при x = |
5 |
5 |
3 |
5 |
2 |
5 |
|
|
|
213 |
|
|
71 |
|
|
|
|
|
|
|
|
|||||||||||
|
, 3 |
|
|
|
+ 2 |
|
− |
|
|
|
−1 = |
|
|
|
|
= |
|
|
>0. |
|
|
|
|
|
|
|||||||
8 |
|
|
8 |
|
192 |
|
64 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
8 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Значит, |
|
корень |
находится |
|
|
внутри |
промежутка |
|
1 |
, |
5 |
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
8 |
|
|||
Можно уже считать, что x = 169 . Если требуется большая
точность, то указанный процесс приближений может быть продолжен дальше.
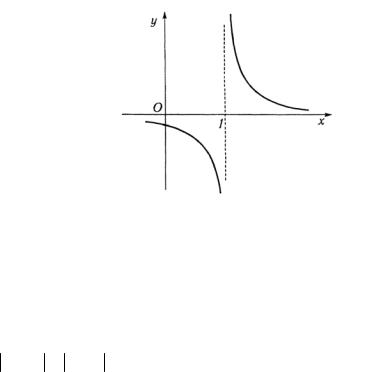
5.6. Определить характер разрыва функций: а) y= x 1−1
при x = 1; б) y= |
x |
|
2x, при |
x ≠ 2, |
|
при x = 0; в) y= |
|
||
x |
|
x = 2. |
||
|
|
1, при |
114
1 |
|
1 |
|
||
г) y= a |
x |
(a>1); д) y=arctg |
и построить графики. |
||
x |
|||||
|
|
|
|
||
Решение. а) При х = 1 функция |
не определена: |
|||||||
lim |
1 |
|
= −∞; |
lim |
|
1 |
|
= +∞ . |
x −1 |
|
|
|
|||||
x→1−0 |
|
x→1+0 x −1 |
|
|||||
Следовательно, при х = 1 функция имеет разрыв второго рода (рис. 1.7).
|
|
|
|
Рис. 1.7 |
|
||||
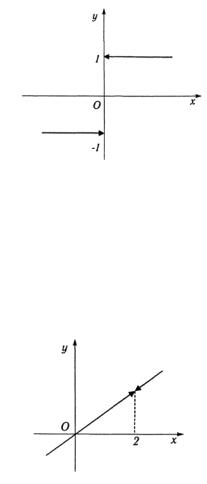
б) При x<0 предел равен lim |
|
x |
|
= −1 = k , при х > 0 предел |
|||||
|
|
|
|||||||
|
|
|
|
x→1−0 |
x |
|
|
1 |
|
|
|
|
|
|
|
|
|||
равен lim |
|
x |
=1 = k2 . Следовательно, при х = 0 функция |
||||||
|
x |
|
|||||||
x→1+0 |
|
|
|
|
|
|
|
|
|
имеет разрыв первого рода и скачок функции равен k1 − k2 = −1 −1 = 2 (рис. 1.8).
115
|
|
Рис. 1.8 |
|
|
|
|
в) Функция |
определена |
на |
всей |
числовой оси, |
||
неэлементарная, |
так как |
в |
точке |
x = 2 |
аналитическое |
|
выражение функции меняется. |
|
|
|
|
||
Исследуем непрерывность функции в точке х = 2: |
||||||
lim 2x = 4 , |
lim 2x = 4 , |
y(2)=1, |
k1 |
= k2 ≠ k3 . |
||
x→2−0 |
x→2+0 |
|
|
|
|
|
Очевидно, что в точке х = 2 функция имеет устранимый разрыв (рис. 1.9).
г) Найдём пределы: |
Рис. 1.9 |
|||
|
|
|
||
1 |
1 |
|
||
y(+0) = lim a |
x |
= +∞, y(-0) = lim a |
x |
= 0. |
x→+0 |
x→−0 |
|||
Вточке x=0 справа функция имеет разрыв второго рода,
аслева — непрерывность (рис. 1.10).
116
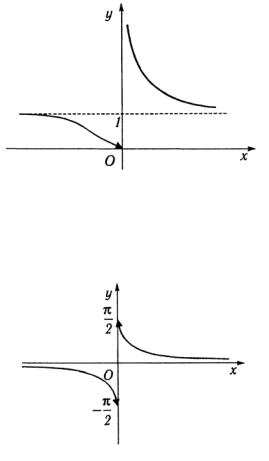
д) Найдем пределы: |
|
|
Рис. 1.10 |
|
|
|
|||
π |
|
|
|
|
π . |
||||
y(+0)= lim arctg |
1 |
= |
, |
y(-0)= lim arctg |
1 |
= − |
|||
x |
2 |
x |
|||||||
x→+0 |
|
|
x→−0 |
|
2 |
||||
В точке x=0 с обеих сторон скачки (рис. 1.11).
|
Рис. 1.11 |
|
|
|
5.7. Дана функция |
1 |
|
|
|
y = |
|
, |
и три значения |
|
x2 + 4x −5 |
||||
аргумента x1 = -5, x2 = 0, |
x3 = 1. Выяснить, |
является ли данная |
||
функция непрерывной или разрывной для каждого из данных
значений х? Сделать чертеж. |
|
|
|
|
|||
Решение. Исследуем |
непрерывность |
функции в точке |
|||||
x = -5: |
1 |
|
|
|
1 |
|
|
lim |
= ∞, lim |
|
|
= −∞ . |
|||
x2 + 4x −5 |
x2 |
+ 4x −5 |
|||||
x→−5−0 |
x→−5+0 |
|
|||||
|
|
117 |
|
|
|
|
|
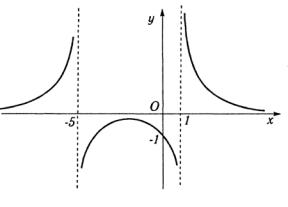
Следовательно, при х1 = -5 функция имеет разрыв второго рода (рис. 1.12).
|
|
|
|
|
|
|
Рис. 1.12 |
|
|
||||
При x2 = 0 пределы слева и справа равны: |
|
||||||||||||
lim |
|
|
1 |
= −1/ 5, |
lim |
|
|
1 |
|
= −1/ 5, |
y(0) = -1/5, |
||
|
|
+ 4x −5 |
|
|
+ 4x −5 |
||||||||
x→−0 x2 |
|
|
|
x→+0 x2 |
|
|
|||||||
следовательно, функция в этой точке непрерывна. |
|
||||||||||||
Исследуем непрерывность функции в точке x3=1: |
|||||||||||||
lim |
|
1 |
|
|
= −∞, |
lim |
|
1 |
|
= ∞. |
|
||
|
2 + 4x −5 |
|
+ 4x −5 |
|
|||||||||
x→1−0 x |
|
x→1+0 x2 |
|
|
|||||||||
Следовательно, при х = 1 функция имеет разрыв второго. |
|||||||||||||
Точки х = 1 и х = -5 |
являются вертикальными асимптотами. |
||||||||||||
5.8.Найти точки разрыва функции, если они существуют,
исделать чертеж:
|
|
2 |
, x ≤1; |
|
|
x |
, x ≤ −1; |
|||||||||
|
x |
|
|
2 |
|
|||||||||||
а) y= |
1, 1 < x ≤ 3; |
б) y= x +1, −1 < x ≤ 0; |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− x + 5, x > 3; |
|
cos x, x > 0. |
|||||||||||||
|
|
|
x = 0 и x = ±3; |
|
2x −1, x < 0; |
|||||||||||
|
3, |
|
||||||||||||||
в) y= |
9 − x2 , 0 < |
|
x |
|
≤ 3; |
г) y= |
|
1 |
|
|
||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, x ≥ 0. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
9, |
|
x |
> 3. |
|
|
x −1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
118
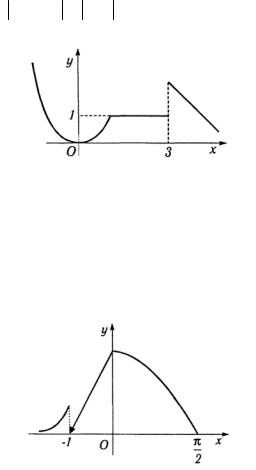
Решение. a) Функция неэлементарная, так как задана тремя аналитическими выражениями на различных промежутках изменения аргумента, определена на всем множестве действительных чисел.
Исследуем непрерывность функции в точках х = 1 и
х = 3: y(1) = lim x2 =1; y(3) =1; |
lim (−x + 5) = 2 = k. |
x→1−0 |
x→3+0 |
Таким образом, в точке х = 1 функция непрерывна, а в точке х = 3 терпит разрыв первого рода (рис. 1.13) и имеет
скачок, равный y(3) − k = 1 − 2 =1.
Рис. 1.13
б) Функция определена на всем множестве чисел и неэлементарная.
Исследуем непрерывность функции в точках х = -1 и х = 0:
y(-1) = |
1 |
, |
lim (x +1) = 0; y(0) =1; |
lim cos x =1. |
|
2 |
|||||
|
|
x→−1+0 |
x→+0 |
Таким образом, функция в точке x = -1 имеет разрыв первого рода, а в точке х = 0 непрерывна (рис. 1.14).
Рис. 1.14
119
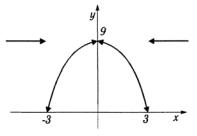
в) Функция определена на всей числовой оси, неэлементарная.
Исследуем непрерывность функции в точках х = - 3 , x=0, x= 3:
y(-3)=3, |
lim |
(9 − x2 ) = 0; y(−3 − 0) = 9; |
|
x→−3+0 |
|
y(0)=3, |
lim (9 − x2 ) = 9; lim y(9 − x2 ) = 9; |
|
|
x→−0 |
x→+0 |
y(3)=3, |
lim |
(9 − x2 ) = 0; y(3 + 0) = 9. |
|
x→3−0 |
|
Таким образом, функция в точках х = -3 и х = 3 имеет разрывы первого рода, а в точке x = 0 устранимый разрыв
(рис. 1.15).
Рис.1.15
г) Функция неэлементарная и определена везде кроме точки x = 1. Исследуем непрерывность функции в точках х = 0
и х = 1:
lim (2x −1) = −1, |
y(0) = −1, lim |
1 |
|
= −∞, lim |
1 |
|
= ∞. |
|
x −1 |
x −1 |
|||||||
x→−0 |
x→−0 |
x→+0 |
|
|||||
Таким образом, |
функция в точке х = 0 непрерывна, а в |
|||||||
точке х = 1 имеет разрыв второго рода (рис. 1.16).
120
