
2619
.pdf
f ′′′(4) = |
3 |
= |
3 |
= |
3 |
. |
|
45 |
8 25 |
256 |
|||||
8 |
|
|
|
||||
Пример 2. Найти производную n-го порядка для функ- |
|||||||
ции y = e3x. |
|
|
|
|
|
|
|
Решение. y' = 3e3x, |
y'' = 3 3e3x = 32e3x, y''' = 33e3x. |
||||||
По аналогии находим: y(n) = 3ne3x.
Рассмотрим механический смысл второй производной.
Пусть путь S, пройденный телом по прямой за время t, выражается формулой S = f (t). Известно, что при этом скорость V в момент времени t равна производной от пути по времени: V = S′(t) . В момент времени t + t скорость получит
приращение
|
|
|
|
|
V = V(t + t) – V(t). |
Отношение |
|
|
V |
называется средним ускорением за вре- |
|
|
|
t |
|||
|
|
|
|
|
|
мя t. Ускорением a |
в данный момент времени называется |
||||
предел среднего ускорения, когда t → 0: |
|||||
a = lim |
|
V |
, |
т.е. a = V'(t) = (S(t))' = S''(t). |
|
|
|
t |
|||
t→0 |
|
|
|
||
Следовательно, ускорение при прямолинейном движении равно второй производной от пути по времени: a = S''(t).
Перейдем к рассмотрению дифференциалов высших порядков.
Пусть y = f (x), x X. Дифференциал этой функции
y = f '(x)dx является функцией от x (если x – не фиксированное число), dx – приращение аргумента x, оно не зависит от x.
Дифференциал от дифференциала функции называется
дифференциалом второго порядка и обозначается d2y или d2f (x).
61

Итак, d2y = d(dy), но dy= f ′(x) dx, поэтому
d2y = d( f ′(x) dx) = ( f ′′(x) dx)dx = f ′′(x) (dx)2.
Будем вместо (dx)2 писать dx2.
Дифференциалом третьего порядка называется диффе-
ренциал от дифференциала второго порядка и обозначается d3y
или d3f (x): d3y = d(d2y) = d( f ′′(x) dx2) = f ′′′(x) dx3 и т.д.
Дифференциалом n-го порядка называется дифференци-
ал от дифференциала (n – 1)-го порядка
d ny = d(d n – 1y) = d(f (n – 1)(x)dxn – 1) = f (n)(x)dxn.
Итак, d |
n |
|
(n) |
n |
(n) |
|
d n y |
|
y = f |
|
(x)dx . Отсюда f |
|
(x) = |
dxn . |
Заметим, что выражение производной через отношение дифференциалов часто бывает удобно, поэтому оно широко используется.
Так, вместо y′x будем писать: dydx , вместо yt′ пишем: dydt .
Пример 3. Найти d3y для функции y = cos2x.
Решение. d 3y = y'''dx3. Вычислим y''', находя последова-
тельно y', y'', y''':
y' = (cos2x)' = –2cosxsinx = –sin2x, y'' = (–sin2x)' = –2cos2x, y''' = 4sin2x. Следовательно, d3y = 4sin2xdx3.
Рассмотрим нахождение производных высших порядков для функций, заданных параметрически и неявно.
Пусть функция y, зависящая от x, задана параметрически уравнениями
x = ϕ(t) , t T
y = g(t)
62
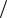
(T – некоторый промежуток). |
|
|
|
|
|
|
|
|
|
|
|
||||
Найдем d 2 y . Известно, что |
dy |
= y′ |
= |
|
yt′ |
, поэтому |
|||||||||
|
|
||||||||||||||
|
dx2 |
|
|
|
|
|
dx |
x |
|
|
xt′ |
||||
|
|
|
|
|
|
|
|
|
|
||||||
d 2 y = ( y′ |
)′ |
= |
( y′x )′t |
= |
(yt′ xt′)′t |
|
= |
yt′′xt′ − xt′′yt′ |
. |
||||||
|
|
|
|||||||||||||
dx2 |
x |
x |
|
x′ |
|
|
x′ |
|
|
|
|
( x′)3 |
|||
|
|
|
|
t |
|
|
|
t |
|
|
|
|
|
t |
|
Аналогично будут вычисляться d 3 y и т.д. dx3
Пример 4. Функция y от x задана параметрически урав-
нениями: x = a cos3 t , |
0≤ t ≤ π. |
|
|
Найти |
d 2 y . |
|||||||||||||||
y = a sin3 t |
|
|
|
|
|
|
|
|
|
|
|
|
dx2 |
|||||||
Решение. |
dy |
= y |
′ = |
yt′ |
|
= |
|
3a sin 2 t cos t |
= –tgt; |
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
dx |
x |
|
xt′ |
|
|
|
−3a cos2 t sin t |
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
d 2 y |
|
|
( y′ |
)′ |
|
|
(−tg t)′ |
|
|
|
|
||||||
|
|
|
|
= |
|
|
x |
|
t |
= |
|
|
|
|
|
= |
|
|
||
|
|
|
dx2 |
|
xt′ |
|
|
|
(a cos3 t)′ |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= - |
|
|
|
1 |
|
|
|
|
|
|
|
|
= |
|
|
1 |
|
. |
||
cos2 t(−3a cos2 t sin t) |
3a cos4 t sin t |
|||||||||||||||||||
Нахождение производных высших порядков от функций, |
||||||||||||||||||||
заданных неявно, рассмотрим на примере. |
|
|
|
|
||||||||||||||||
Пример 5. Найти |
dy |
|
, |
d 2 y |
для функции, заданной неяв- |
|||||||||||||||
dx |
dx2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
но уравнением: ey + xy = e. |
|
Вычислить y'(0), y''(0). |
||||||||||||||||||
Решение. Найдем сначала y', как описано в в разд. 2.5: |
||||||||||||||||||||
(ey + xy)' = (e)', |
ey y' + y + xy' = 0, |
y'(ey + x) = –y, |
||||||||||||||||||
63

y
y' = – e y + x .
Для нахождения y'' будем дифференцировать равенство ey y' + y + xy' = 0, получим:
ey (y')2 + ey y'' + y' + y' + xy'' = 0,
отсюда найдем y'', затем подставим найденное значение y':
|
|
|
y''(ey + x) = –ey (y')2 – 2y', |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
y 2 |
|
|
y |
||||
y'' = – e y ( y′)2 + 2 y′ |
|
e y |
− |
|
|
|
+ 2 |
− |
|
|
|
||||||
|
|
|
|
|
|||||||||||||
= − |
|
|
|
|
e y + x |
|
|
e y + x |
= |
||||||||
|
|
|
|
e y + x |
|
|
|||||||||||
|
e y + x |
|
|
|
|
|
|
|
|
|
|
|
|||||
= |
− e y y2 |
+ 2 y(e y + x) |
= |
|
− e y y2 + 2e y y + 2 yx |
. |
|
|
|||||||||
(e y + x)3 |
|
|
|
|
(e y |
+ x)3 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
Итак, y' = – |
|
y |
, |
y'' = |
− e y y2 + 2e y y + 2 yx |
. |
|
|
|
||||||||
e y + x |
|
|
|
|
(e y + x)3 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Подставим x = |
0 в исходное уравнение ey + xy = e, |
получим: |
||||||||
ey + 0 y = e, откуда |
|
y = 1, значит, |
|
|
|
|
||||
y(0) = 1; |
y'(0) = – |
1 |
|
; |
y''(0) = |
e |
= |
|
1 |
. |
e |
(e) 3 |
|
|
|||||||
|
|
|
|
|
e2 |
|||||
2.9. Основные теоремы о дифференцируемых функциях
Теорема Ферма. Пусть функция f (x) определена, непрерывна на интервале (a, b) и в некоторой точке x0 этого интервала принимает свое наибольшее или наименьшее значение. Если в точке x0 существует производная этой функции, то f ′(x0 ) = 0.
64
Доказательство. Пусть f (x0) = M – наибольшее значение функции на (a, b). Покажем, что f '(x0) = 0. По определению производной
|
|
f |
′(x |
0 |
) = |
lim |
f (x0 + |
x) − f ( x0 ) |
. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
x→0 |
x |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Так как f (x0) – наибольшее значение, то при любом знаке |
x |
|||||||||||||||||
имеем |
f(x0 + |
x) |
|
– f(x0) ≤ 0. Отсюда, если |
x > |
|
0, |
то |
||||||||||
|
f ( x0 + |
x) − f (x0 ) |
|
≤ 0, |
а поэтому |
f ′(x |
0 |
) ≤ 0 (см. раздел 1). |
||||||||||
|
|
x |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если |
x < 0, то |
|
f (x0 + |
x) − f (x0 ) |
≥ 0, |
|
поэтому |
f ′(x |
0 |
) ≥ 0. |
||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так как f ′(x0 ) – определенное число, то получаем, что f ′(x0 ) = 0. Теорема доказана.
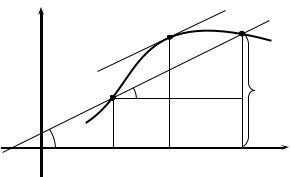
Геометрически теорему Ферма поясняет рис. 2.7. В точке x1 функция принимает наибольшее значение M, а в точке x2 – наименьшее значение m, касательные к графику y = f (x) в точках A и B параллельны оси Ox, так как f '(x1) = 0 и f '(x2) = 0.
Теорема Ролля. Если функция f (x) непрерывна на отрезке [a, b], дифференцируема в каждой внутренней точке и f(a) = f(b), то существует, по крайней мере, одна внутренняя точка x0 отрезка [a, b], что f'(x0) = 0.
Доказательство. Так как функция непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наибольшего значения M и своего наименьшего значения m (см. раздел 1)
Если M = m, то функция f (x) постоянна на отрезке [a, b], а потому f '(x) = 0 для любого x (a, b).
Рассмотрим случай, когда M ≠ m. Так как f(a) = f(b), то либо M ≠ f(a), либо m ≠ f(a), тогда либо наибольшее значение M, либо наименьшее значение m достигается во внутренней точке x0, x0 (a, b).
65
y
M0
y = f(x) 
f(a) =
0 |
a |
x0 |
b |
x |
|
Рис. 2.7
Следовательно, по теореме Ферма
f ′(x0 ) = 0. Теорема доказана.
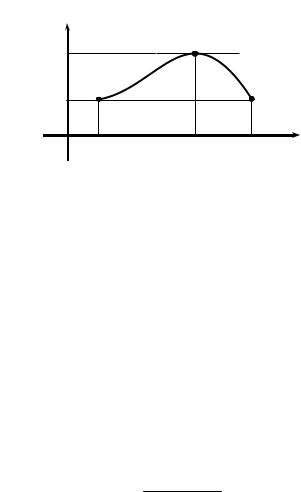
Геометрически теорема Ролля утверждает (рис. 2.8), что если функция непрерывная на [a, b] и дифференцируемая на (a, b), имеет на концах отрезка [a, b] одинаковые значения, то найдется точка x0 (a, b), для которой касательная к графику параллельна оси абсцисс.
Теорема Лагранжа. Если функция f (x) непрерывна на отрезке [a, b], дифференцируема на интервале (a, b), то найдется хотя бы одна внутренняя точка x0 отрезка [a, b], такая, что
f ′(x ) =. |
f (b) − f (a) |
. |
(2.14) |
0 |
b − a |
|
|
|
|
||
Доказательство. Рассмотрим вспомогательную функ-
цию:
F(x) = f(x) – f (b) − f (a) (x – a) b − a
и покажем, что она удовлетворяет условиям теоремы Ролля. Функция F(x) непрерывна на [a, b], так как на [a, b] непрерывны функции f (x) и (x – a). Производная
F'(x) = f ′(x) – |
f (b) − f (a) |
(2.15) |
|
b − a |
|||
|
|
существует в интервале (a, b). Вычислим F(x) на концах отрез-
ка [a, b]:
66
F(a) = f (a) – f (b) − f (a) (a – a) = f (a), b − a
F(b) = f (b) – f (b) − f (a) (b – a) = f (b) – f (b) + f (a) = f (a). b − a
y M
|
|
y = f ( x |
|
m |
|
|
|
0 a |
x1 |
x2 |
b x |
|
Рис. 2.8 |
|
|
Значит, F(a) = F(b). По теореме Ролля найдется точка x0 (a, b), такая, что F'(x0) = 0. Подставив x0 в равенство (2.15)
получи F'(x0) = |
f ′(x |
0 |
) – |
|
f (b) − f (a) |
, откуда |
||||
|
|
|
||||||||
|
|
|
|
|
|
b − a |
||||
|
|
|
|
|
|
|
||||
|
|
f |
′(x |
0 |
) = |
f (b) − f (a) |
. Теорема доказана. |
|||
|
|
|
|
|
|
|
b − a |
|||
|
|
|
|
|
|
|
|
|||
Поясним теорему Лагранжа геометрически (рис. 2.9). |
||||||||||
Отношение |
|
f (b) − f (a) |
есть угловой коэффициент tgα |
|||||||
|
|
b − a |
||||||||
|
|
|
|
|
|
|||||
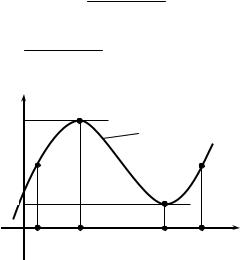
хорды AB, соединяющей точки A(a, f (a)), B(b, f (b)), f '(x0) – угловой коэффициент касательной к графику y = f (x), прове-
денной в точке M0(x0, f (x0)), и f ′(x0 ) = tgα. Теорема Лагранжа
утверждает, что на графике функции y = f (x) найдется хотя бы одна точка M0, в которой касательная к графику параллельна хорде AB.
Заметим, что формулу (2.14) можно записать в виде:
f (b) – f (a) = f ′(x |
0 |
) (b – a). |
(2.16) |
|
|
|
67
y |
M0 |
B |
|
||
|
A α |
f(b) |
α f(a)
f(a)
|
0 |
|
|
a |
|
|
x0 |
|
|
b |
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
Рис. 2.9 |
|
|
|
|
|
|||
Обозначив x0 = c, |
a = x0, |
b – a = |
x, |
b = x0 + |
x, из формулы |
|||||||||
(2.16) получаем формулу: |
|
|
|
|
f ′(c) x. |
|
|
|
||||||
|
|
f (x0 + x) – f (x0) = |
|
(2.17) |
||||||||||
Формулы (2.16), (2.17) называют формулами конечных приращений, а теорему Лагранжа – теоремой о конечных приращениях. При этом теорема Лагранжа переформулируется следующим образом: приращение дифференцируемой функ-
ции на отрезке равно произведению длины отрезка на значение производной этой функции в некоторой внутренней точке отрезка.
Получим следствие из теоремы Лагранжа. Известно, что производная постоянной функции равна нулю. Докажем обратное утверждение.
Следствие. Если функция f (x) непрерывна на отрезке [a, b] и во всех внутренних точках этого отрезка f ′(x) = 0, то
функция f (x) постоянна на отрезке [a, b].
Доказательство. Пусть x – произвольная точка отрезка [a, b], не совпадающая с a, тогда по формуле (2.16) конечных приращений применительно к отрезку [a, x] имеем:
f (x) – f (a) = f ′(x0)(x – a), |
где x0 (a, x). |
|
Но f ′(x0) = 0, |
поэтому f (x) = f (a). Следовательно, |
|
x [a, b]: |
f (x) = f (a) и |
f (x) – постоянна на [a, b]. |
68

Теорема Коши. Пусть функции f(x), g(x) непрерывны на отрезке [a, b], дифференцируемы на (a, b), причем g'(x) ≠ 0 для любой точки x из интервала (a, b). Тогда существует внутрен-
няя точка x0 отрезка [a, b], такая, что |
|
|
|
|||
|
f (b) − f (a) |
= |
f ′(x0 ) |
. |
||
|
ϕ(b) −ϕ(a) |
|
||||
|
|
ϕ′(x |
0 |
) |
|
|
|
|
|
|
|
|
|
Доказательство. Отметим, что ϕ(b) ≠ ϕ(a), так как в противном случае по теореме Ролля ϕ'(x) = 0 в некоторой точке x0 (a, b).
Введем вспомогательную функцию:
F(x) = f (x) – f (b) − f (a) (ϕ(x) – ϕ(a)) ϕ(b) −ϕ(a)
и покажем, что F(x) удовлетворяет теореме Ролля. Очевидно,
что F(x) непрерывна на отрезке [a, b], |
дифференцируема на |
|||||||||||||
(a, b) |
и F'(x) = f'(x) – |
f (b) − f (a) |
ϕ′(x) , и на концах отрезка |
|||||||||||
ϕ(b) −ϕ(a) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
[a, b] |
имеет равные значения: F(a) = f (a), |
F(b) = f (a). |
||||||||||||
|
Следовательно, по теореме Ролля найдется точка |
|||||||||||||
|
x0 (a, b) такая, что F'(x0) = 0: |
|
|
|
||||||||||
|
F'(x0) = f ′(x0) – |
|
f (b) − f (a) |
ϕ |
′(x |
0 |
) = 0. |
|||||||
|
|
ϕ(b) −ϕ(a) |
||||||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
Отсюда |
f (b) − f (a) |
= |
f ′(x0 ) |
. |
Теорема доказана. |
||||||||
|
ϕ(b) −ϕ(a) |
|
||||||||||||
|
|
|
|
ϕ′(x |
0 |
) |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Теоремы Ферма, Ролля, Лагранжа, Коши будут многократно применяться на протяжении курса математического анализа.
69

2.10.Правило Лопиталя
Вразделе 1 мы познакомились с приемами нахождения пределов отношения двух бесконечно малых или бесконечно
больших функций, т.е. раскрытия неопределенностей типа 00 и
∞∞ . В этом разделе мы рассмотрим новый способ вычисления
таких пределов, так называемое правило Лопиталя. Теорема Лопиталя. (Раскрытие неопределенностей типа 00 )
Пусть функции f(x), g(x) определены, непрерывны и дифференцируемы в точке x0 и некоторой ее окрестности, причем g'(x) ≠ 0 для любого x из этой окрестности, и пусть f(x0) = 0, g(x0) = 0 (следовательно, f(x), g(x) – бесконечно малые
при |
x → x0 ). Если lim |
|
f ′(x) |
существует, |
то существует |
||||||||
|
|
x→x |
0 |
g′( x) |
|
|
|
|
|
|
|||
|
f (x) |
|
|
|
|
|
|
|
|
|
|
||
lim |
и |
|
|
|
|
|
|
|
|
|
|
|
|
x→x0 |
g(x) |
|
|
f (x) |
|
|
|
|
f ′(x) |
|
|
||
|
|
lim |
|
= |
lim |
. |
(2.18) |
||||||
|
|
x→x |
0 |
|
g(x) |
|
|
x→x |
0 |
g′( x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доказательство. Равенство (2.18) называют правилом
Лопиталя для раскрытия неопределенностей типа 0 .
0
Дадим значению аргумента x0 приращение x, такое, чтобы точка x = x0 + x принадлежала рассматриваемой окрестности точки x0.
Случай 1. x > 0, тогда x > x0. Функции f (x), g (x), рассматриваемые на отрезке [x0, x], удовлетворяют теореме Коши,
поэтому найдется |
такое c (x0, x), что выполняется равенст- |
||||
во: |
f (x) − f (x ) |
= |
f ′(c) |
. Так как f (x0) = g(x0) = 0, то получим: |
|
0 |
|
||||
g(x) − g(x ) |
g ′(c) |
||||
|
|
|
|||
|
0 |
|
|
|
|
70
