
2619
.pdf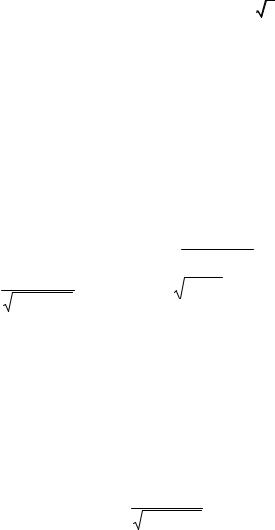
|
|
|
|
|
|
|
= 1 x3 − |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
y |
3x−2 + 4x2 −5, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
2 |
|
|
|
−3 |
|
|
|
|
− |
1 |
|
|
3 |
2 |
6 |
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
y′ = 2 x |
|
+6x |
|
+ 2x |
|
2 = |
|
2 x |
|
|
+ |
|
+ |
|
|
|
. |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
x |
||||||||||||||||||||
б) Здесь имеет место случай произведения двух функций, |
|||||||||||||||||||||||||||||||||||
поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y |
′ |
= |
3 |
|
′ |
|
3 |
|
|
|
|
′ |
= 3x |
2 |
cos x − x |
3 |
sin x. |
|
|
|
|
|
|
||||||||||||
|
(x |
|
) cos x + x |
(cos x) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
в) Поскольку имеет место частное двух функций, то |
|||||||||||||||||||||||||||||||||||
|
′ |
|
(x |
2 |
′ |
2 |
+1) − (x |
2 |
)(x |
2 |
|
′ |
|
|
|
|
2x |
3 |
+ 2x − 2x |
3 |
|
|
|
2x |
|||||||||||
y |
= |
|
|
) (x |
|
|
|
+1) |
|
= |
|
|
|
|
|
= |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||
|
|
|
|
|
|
(x2 +1)2 |
|
|
|
|
|
|
|
|
(x2 +1)2 |
|
|
(x2 +1)2 |
|||||||||||||||||
г) Находим производную f'{x) = x2 - 2х и вычисляем ее значения в точках x = 0, х = 1, х = - 1 , т. е. находим частные значения производной в этих точках:
f |
′ |
= 0, |
f |
′ |
= −1, |
f |
′ |
= 3. |
(0) |
(1) |
(−1) |
1.5.Найти производные: а) y = ln x2 − 4x + 4 ;
x2 + 4x + 4
б) |
y = ln |
x +1 |
; |
|
в) |
|
y = log2 |
3 tg 2 2x; |
|
|
|
|
|
|||||
|
|
x2 − x + |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
г) |
y = ln3 cos |
x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. a) Упростим логарифмируемое выражение |
|
|
|
|||||||||||||||
|
x − 2 |
2 |
|
|
x − 2 |
|
|
|
|
|
x − 2 |
|
||||||
y = ln |
|
= 2ln |
|
|
. |
Полагая у = 2ln и, |
u = |
|
|
, |
||||||||
|
x + 2 |
x + 2 |
||||||||||||||||
|
x + 2 |
|
|
|
|
|
|
|
|
|
||||||||
применяем правило дифференцирования сложной функции |
|
|||||||||||||||||
y′ = 2(ln u)′u u′x = 2 |
x + 2 |
|
|
(x − 2)′(x + 2) − (x − 2)(x + 2)′ |
= |
|
|
8 |
. |
|||||||||
x − 2 |
|
x2 |
− 4 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
(x + 2)2 |
|
|
|||||||
б) Полагая у = lп и, где и = |
x +1 |
, имеем |
x2 − x +1 |
||
y′ = 2(ln u)′u u′x = |
|
|
131
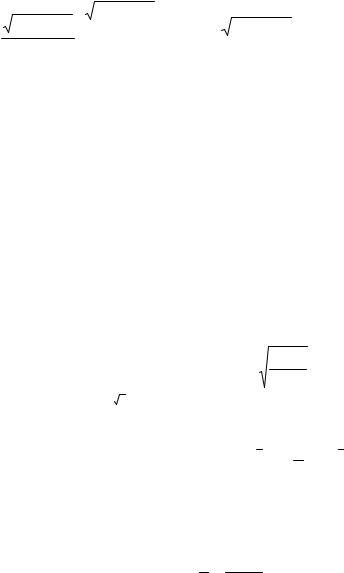
|
|
|
|
|
|
|
|
x2 − x +1 − (x +1) |
2x −1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
= |
|
|
x2 − x +1 |
|
2 x2 − x +1 |
= |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
x +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 − x +1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= |
3 |
|
|
|
1 − x |
= |
|
3 1 − x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 (x +1)(x2 − x +1) |
|
2 (x +1)3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
в) Упростим логарифмируемое выражение |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y = log2 tg |
3 |
2x = |
log2 tg2x. |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Дифференцируем как сложную функцию |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
8 |
|
|
|
|
1 |
|
|
||||||||||
|
|
|
|
|
|
|
y′ = 3 |
|
|
|
|
|
|
2 |
= 3 |
|
|
|
|
|
. |
||||||||||||||||||
|
|
|
|
|
|
|
tg2x ln 2 |
cos2 2x |
sin 4x ln 2 |
||||||||||||||||||||||||||||||
|
|
г) Дифференцируем как сложную функцию |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
′ |
|
2 |
|
|
x |
|
|
1 |
|
|
|
|
|
|
|
|
x |
|
1 |
|
|
|
|
|
x |
|
2 |
|
|
x |
|
||||
|
|
|
y |
= 3ln |
|
cos 3 cos |
x |
|
(−sin 3) 3 = −tg 3 ln |
|
|
|
cos 3 . |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|||
|
|
1.6. Найти производные: а) z = xea |
+ ae |
a ; |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
б) |
y = e−3x (sin 3x + cos3x) ; в) z = ln |
|
1 − 2x |
; |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + 2x |
|
|
|
|
|||||
г) y = esin 3 |
x + 55 |
x . |
|
|
|
|
|
|
|
|
||||
Решение. |
|
|
a) |
Дифференцируем |
||||||||||
|
|
x |
|
x |
1 |
− |
x |
|
|
1 |
|
|||
|
|
|
|
|
|
|
a |
|
|
|||||
функций z′ = ea + xea |
|
|
||||||||||||
|
+ ae |
|
− |
|
|
= |
||||||||
a |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
||
как сумму сложных eax 1+ ax −e−ax .
б) Дифференцируем как произведение сложных функций y′ = e−3x (−3)(sin 3x + cos3x) + e−3x (cos3x 3 + (−sin 3x) 3) =
= −6e−3x sin 3x.
в) Упростим функцию y = 1 ln 1 − 2x . 2 1 + 2x
Находим производную как от сложной функции
132
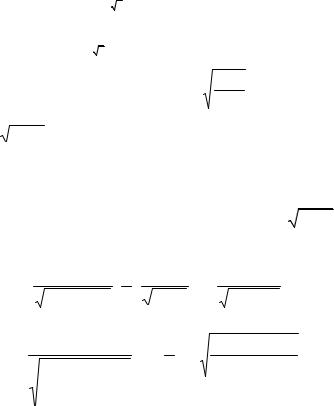
y′ = |
1 |
|
1+ 2x |
− |
2x ln 2(1+ 2x ) +(1−2x )2x ln 2 |
= |
2x ln 2 |
2 |
1−2x |
(1+ 2x )2 |
22 x −1. |
г) Дифференцируем как сумму сложных функций
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y′ = esin3 x 3sin2 x cos x +53 x ln 5 |
x−5 = |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 3esin3 x sin2 x cos x +53 x −1 x−5 ln 5. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
1.7. Найти производные: а) |
|
y = arctg |
1 − x ; |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + x |
|
|
|
|
x |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 −3ϕ |
|
; г) y = 3arctge− |
|
||||||||||||||||||
б) u = arcsin 1 − 4t ; в) r = arccos |
|
|
. |
|
|||||||||||||||||||||||||||||||||||||||
3 |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. а) Находим производную как от сложной |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
1 |
|
1− x − |
1 |
|
|
−(1+ x) −(1− x) |
|
|
|
|
1 |
|
||||||||||||||||||||||
функции y′ = |
|
|
|
|
|
|
|
2 |
|
= − |
|
|
|
. |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
1− x |
2 |
|
|
|
|
|
(1+ x) |
|
|
2 1− x2 |
||||||||||||||||||||||||||||||
1+ |
|
|
1+ x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
1+ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
б) Производная равна |
|
|
|
|
|
|
|
(−4) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
u |
′ |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||||||
= 1 − (1 |
− 4t) 2 |
1 − 4t = − t(1 − 4t) . |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
в) Производная равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
r′ = − |
|
|
|
1 |
|
|
|
|
|
|
|
− |
3 |
|
|
3 |
|
|
. |
|
|
||||||||||||||||||||||
|
|
|
|
|
− 3ϕ 2 |
|
4 |
= |
4 + 4ϕ − 3ϕ |
2 |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
1 − |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
г) Производная равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
(−1) |
|
|
|
|
x |
|
|
|
1 |
|
|
|
|
|
e− |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
y′ = 3 |
|
|
|
e |
− |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
− |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1 + e− |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
1 + e− |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
1.8. Найти производные: а) |
|
y = sh2 |
x |
+ ch2 |
x |
|
; |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|||||||
б) y = thx+cthx.
Решение. а) Дифференцируем как сумму
133
|
|
|
′ |
|
|
|
|
|
x |
|
|
x |
|
|
1 |
|
|
x |
|
|
|
x |
|
1 |
|
|
|
|
|
|
|
|
||
|
y |
= 2sh 2 ch 2 |
2 |
+ 2ch 2 ch 2 2 = shx. |
||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
б) Дифференцируя как сумму и пользуясь свойствами |
||||||||||||||||||||||||||||||||||
гиперболических функций, имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
sh2 x − ch2 x |
4 |
|
|||||||||||||||||||
y′ = |
|
− |
|
= |
|
|
|
|
= − |
|
|
|
|
|
. |
|||||||||||||||||||
ch2 x |
sh2 x |
|
sh2 xch2 x |
|
|
sh2 2x |
||||||||||||||||||||||||||||
1.9. Найти производные: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xe−x , |
|
x |
|
≤ 0; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
x |
|
, |
|
x |
< 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а) y = |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
, |
|
б) y = |
|
1 |
|
|
|
|
, |
|||||||||||
|
|
|
|
|
|
), |
|
|
x ≥ 0 |
|
|
|
, |
|
|
|
x |
> 0 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
ln(1 + x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
2 − x, −1 < x < 2; |
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 −5x + 6, 2 ≤ x |
≤ 3; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
в) y = x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
−3, |
3 < x < 4, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
построить график функции и производной.
Решение. а) Поскольку функция на разных участках имеет различный вид, то для этих участков
2x, |
|
x < 0; |
|||
|
2x |
|
|
|
|
y′ = |
|
|
, x ≥ 0. |
||
|
|
|
|
|
|
|
+ x |
2 |
|
||
1 |
|
|
|
||
б) Находим производную на разных участках
|
−x |
(1 − x), |
|
x |
|
≤ 0; |
|||
|
|
||||||||
e |
|
|
|||||||
y′ = |
|
|
x |
|
> 0. |
||||
0, |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) Находим производную на разных участках
−1, |
−1 ≤ x ≤ 2; |
|
|
y′ = 2x −5, 2 ≤ x ≤ 3; |
|
|
< x < 4. |
1, 3 |
|
Строим график функции и график производной (рис.2.4).
134

Рис. 2.4
1.10. Найти производные: а) y= |sinx|; б) y= |arctgx|.
Решение. а) График функции у = |sinx| показан на рис. 2.5.
Если |
x (πk,π(k +1)) , |
то данную функцию можно |
||
записать |
в |
виде y = sin (x −πk) . |
Отсюда производная |
|
y′ = cos(x −πk) . |
|
|
||
Если х = πk , то y−′(πk) = |
lim |
cos(x −πk) = −1, |
||
|
|
|
x→π (k +1)−0 |
|
y+′ (πk) = |
lim |
cos(x −πk) =1. |
|
|
|
x→πk +0 |
|
|
|
Рис. 2.5
б) Представим график функции y = |агсtgx| на рис. 2.6 и
arctgx, x ≥ 0;
запишем функцию в виде y =
− arctgx, x < 0.
135

Рис. 2.6
Производная для различных участков будет
|
1 |
|
, |
x ≥ 0; |
||||
|
|
|
|
|
||||
|
+ x |
2 |
||||||
y′ = 1 |
|
|
|
|
|
|||
|
1 |
|
|
|
, x < 0, |
|||
− |
|
|
|
|
|
|
||
1 + x |
2 |
|
||||||
|
|
|
|
|||||
|
|
|
y−′(0) = |
|
|
|
1 |
|
|
||
производная слева |
lim |
− |
|
|
|
= −1; |
|||||
|
|
|
|||||||||
|
|
|
1 |
|
x→−0 |
|
1 + x2 |
||||
справа |
y+′ (0) = lim |
|
=1. |
|
|
|
|
|
|||
1 + x2 |
|
|
|
|
|
||||||
|
|
x→+0 |
|
|
|
|
|
|
|
||
1.11. Найти производные функций, обратных к заданным: |
|||||||||||
а) y = sh x; б) y = ch х; в) у = th х; г) y = cth х. |
|||||||||||
Решение. а) По правилу дифференцирования обратной |
|||||||||||
функции получим |
|
|
|
|
|
|
|
|
|
||
|
′ |
1 |
1 |
|
|
1 |
|
|
|
1 |
|
( Arshy) = y′x = chx = |
1 + sh2 x |
= |
y2 +1 , |
||||||||
отсюда, переходя к обычным обозначениям, имеем |
|||||||||||
|
′ |
1 |
|
|
|
|
|
|
|
|
|
( Arshx) = |
1 + x2 . |
|
|
|
|
|
|
|
|||
б) По правилам дифференцирования обратной функции |
|||||||||||
|
′ |
1 |
1 |
|
|
1 |
|
|
|
|
|
имеем |
( Archy) |
= y′x |
= shx |
= |
y2 −1 |
, |
|
|
|||
|
|
|
|
|
|
136 |
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
1 |
|
|
|
|
, |
|
|
( x >1). |
|
|
|
|
|
|
|
|
|
|
|||||||||||
откуда ( Archx) |
= |
|
x2 −1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
в) |
производная |
|
|
|
|
|
|
|
|
обратной |
|
|
|
функции |
равна |
||||||||||||||||||||||||||||||
|
|
′ |
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
( Arthy) = |
|
|
|
|
= ch |
|
x = |
|
|
|
|
|
|
|
|
= |
|
|
, |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
y′x |
|
|
1 −tg 2 x |
1 − y2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
откуда ( Arthx)′ |
= |
|
1 |
|
|
|
|
, |
( |
|
x |
|
<1). |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
1 − x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
г) |
производная |
|
|
|
|
|
|
|
|
обратной |
|
|
|
функции |
равна |
||||||||||||||||||||||||||||||
|
|
′ |
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||
( Arcthy) = |
|
|
|
|
= −sh |
|
x |
|
= − |
|
|
|
|
|
= − |
|
|
, |
|
|
|
|
|||||||||||||||||||||||
y′x |
|
|
|
ctg 2 x −1 |
y2 −1 |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
( |
|
x |
|
>1). |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
откуда ( Arcthx) |
|
= − x2 −1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1.12. Пользуясь результатами предыдущего примера, |
|||||||||||||||||||||||||||||||||||||||||||||
найти производные: а) y = Archln х; б) y = Arcth |
2x |
|
. |
||||||||||||||||||||||||||||||||||||||||||
x2 +1 |
|||||||||||||||||||||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
а) По |
|
правилу дифференцирования |
сложных |
|||||||||||||||||||||||||||||||||||||||||
функций имеем y |
′ |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||||||
= |
|
|
|
|
ln2 −1 |
|
x = x |
ln2 x −1 . |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
б) Функция сложная, поэтому |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
y |
′ |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2(x2 +1) − 2x 2x |
|
|
2(x2 +1) |
|
|
|||||||||||||||||||||
= − 2x |
|
2 |
|
|
|
|
|
|
|
|
|
|
(x2 +1)2 |
|
|
|
= − (x2 −1)2 . |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
x2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2.2. Производные функций, не являющихся явно заданными
10. Пусть функция y задана уравнением f(х,у) = 0, не разрешенным относительно у, то есть у есть неявная функция
от х. |
y |
Чтобы найти производную от неявной функции |
аргумента x дифференцируем по х обе части этого равенства, считая у функцией x. Из полученного равенства определяем
137

искомую производную y', которая, как правило, будет зависеть
oт |
x и y |
|
|
|
у’=ϕ (х ,у). |
|
|
|
|
|
|||
|
|
20. Если |
|
|
|
|
|
|
|
||||
|
|
|
функциональная |
зависимость |
между |
||||||||
переменными x |
и y |
задана параметрически |
|
|
|
||||||||
|
|
|
|
|
|
|
x = ϕ(t); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y =ψ (t), |
yt′ |
|
|
xt′ |
|
|
то производная от y |
по x: равна y′x = |
|
, а от х по y: |
x′y = |
. |
||||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
xt′ |
|
yt′ |
||
|
|
30. Логарифмическое дифференцирование. Если y = uv, то |
|||||||||||
y |
′ |
= vu |
v −1 ′ |
v |
|
′ |
|
|
|
|
|
|
|
|
u |
+ u |
v ln u, т. е. производная показательно-степенной |
||||||||||
функции состоит из двух слагаемых: первое получается, если рассматривать функцию при дифференцировании как степенную, второе как показательную.
40. Если основание логарифма logv и является некоторой функцией x, то при нахождении производной целесообразно перейти к натуральным логарифмам
y= logv u = lnlnuv , u=u(x), v=v(x).
2.1.Найти производные y′x : а) y = cos(x+y);
б) ey + 4xy − x2 =1; и производные х’y: в) xlny-ylnx = 1;
г) х2у2 - 4lnу = 2lпх.
Решение. а) Дифференцируем обе части по х, считая y сложной функцией, зависящей от х
y’=-sin(x+y)(1+y’)=-sin(x+y)-y’sin(x+y). Откуда y’ (1 + sin(x + y)) = - sin(x+y)
|
y |
′ |
|
|
sin(x + y) |
|
|
или |
= −1 |
+ sin(x + y) . |
|||||
|
|||||||
б) Дифференцируя обе части равенства по х, получим eyy’+ 4(y+xy’) - 2x = 0.
Разрешая равенство относительно y', получим
138
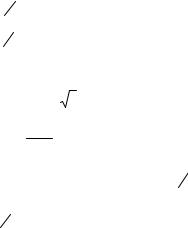
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′ = |
|
2(x − 2 y) |
. |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ey + 4x |
|
|
|
|
|
|
|
|||||||||||||||
в) Дифференцируем обе части равенства по у, считая х |
|||||||||||||||||||||||||||||||||||||||||||
сложной функцией, зависящей от y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
′ |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
y − (ln x + y x |
|
|
= 0. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x ln y |
|
x ) |
||||||||||||||||||||||||||||||||
Разрешая равенство относительно х', получим |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln x − |
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
′ |
= |
y |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln y − |
|
|
y . |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
г) Дифференцируем обе части равенства по у |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
2 |
|
+ 2x |
2 |
y |
− |
4 |
|
= 2 |
|
1 |
|
′ |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2xx y |
|
|
|
|
|
|
x x . |
|
|||||||||||||||||||||||||
|
|
|
|
|
2 |
− x2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
′ |
|
|
y |
|
|
x(2 − x2 y2 ) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Отсюда |
|
x = |
|
|
|
|
= |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
xy2 − |
1 |
|
y(x2 y2 −1) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2.2. Найти производные у'x: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
32 |
t; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
= e |
cos 2t |
; |
|
|
|
|||||||||||||
а) |
x = cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
32t; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ln sin t; |
|
|
|||||||||||||||||||
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|||||||||||||||||
|
|
y = sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и производные х’y: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= tg ϕ ; |
|
|
|||||||||||||||||||||
|
|
|
|
x = arctg |
t ; |
|
|
|
|
|
|
|
|
x |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
г) |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||
|
|
|
в) |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
||||||||
|
|
|
|
y = |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ln cos |
. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
1 + t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. а) Находим |
|
|
|
|
= − |
3 |
cos 12 t sin t и |
||||||||||||||||||||||||||||||||||||
|
|
|
dt |
|
2 |
||||||||||||||||||||||||||||||||||||||
|
dy |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
= |
sin 12 t cost . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
dt |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
139
3 sin 12 t cost |
|
Отсюда y′ = 2 |
= − ctgt . |
−32 cos 12 t sin t
6)Находим dxdt = −2ecos 2t sin 2t и dydt = cossin tt = ctgt .x
Отсюда y′x |
= − |
|
|
|
|
1 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
4ecos 2t |
sin2 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
в) |
Находим |
|
|
dy |
= |
2t(1 + t) −t2 |
= |
t2 |
+ 2t |
|
|
и |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
dt |
|
|
(1 + t)2 |
|
(1 |
+ t)2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
= |
|
2 t |
= |
|
|
|
|
|
1 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
1 + t |
|
2 |
|
t (1 + t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Отсюда |
|
dx |
= |
|
|
|
|
|
(1 + t)2 |
|
|
|
|
= |
|
|
|
1 + t |
|
|
|
. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
dy |
|
2 |
|
t (1 + t)t(t + |
2) |
|
|
2t 32 (t + 2) |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
dy |
|
|
|
|
1 sin |
ϕ |
|
|
|
|
|
1 |
|
|
|
ϕ |
|
|
|
dx |
|
1 |
1 |
|
|
|||||||||
г) Находим |
|
= − |
2 |
|
|
= − |
|
tg |
и |
|
|
= |
|
. |
|||||||||||||||||||||||||
dϕ |
|
2 |
|
|
|
ϕ |
|
|
|
|
|
dϕ |
2 |
|
|
2 ϕ |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
2 2 |
|
|
|
|
cos |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Отсюда |
|
x′y |
= − |
|
|
|
|
2 |
|
|
|
|
|
= − |
|
2 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2cos |
2 |
ϕ |
tg |
ϕ |
sinϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2.3. Найти производные: a) y = xx2 ; б) |
y = xsin 2 x ; |
|
|
|
|||||||||||||||||||||||||||||||||||
в) y = (x −1)2 3 |
x + 2 ; |
|
г) |
y = x2ex3 |
sin 3xthx . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
(x −3)3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. а) Прологарифмируем правую и левую часть lny = x2lnx.
Найдем производные от правой и левой части по x, считая y сложной функцией, зависящей от х
140
