x3x4 x5

000 001 011 010 110 111 101 100

00

01 x1x2 11

10

Рис 6.6. Карта Карно для функции пяти переменных

6.4.3. Аналитическая форма представления логических функций

Табличные способы задания логических функций становятся весьма громоздкими с увеличением числа аргументов. Так, уже при восьми аргументах количество строк в таблице истинности или количество клеток карты Карно равно 256. Аналитические формы представления логических функций более компактны и наглядны, и позволяют очень просто синтезировать комбинационные автоматы из ограниченного количества логических элементов, реализующих логические операции умножения (конъюнкцию), сложения (дизъюнкцию) и отрицания (инверсию). В то же время, аналитические формы логических функций позволяют выполнять различные их математические преобразования с целью получения более простых соотношений или для каких-либо других целей.

Аналитический способ предусматривает запись логической функции в форме логического выражения, показывающего, какие логические операции над аргументами должны выполняться и в какой последовательности. Сложные функции от многих аргументов могут быть представлены в форме "функций от функций", т.е. выражаться через более простые функ-

86

ции от меньшего числа аргументов. Так, если z = z(x, y); x = x (a, b); y = y (c, d), то z = z (a, b, c, d). Операция замены ар-

гументов одной функции другими, более простыми функциями носит название суперпозиции функции. Многократное использование принципа суперпозиции дает возможность получить функции желаемого числа аргументов.

Для аналитического задания логических функций используются, так называемые, нормальные формы.

В алгебре логики существует две самые распространенные аналитические формы представления функции: совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальная форма (СКНФ). Каждая логическая функция имеет одну СДНФ и одну СКНФ.

СДНФ логической функции может быть получена путем многократного применения теоремы разложения (6.25) к некоторой функции n аргументов для каждой ее переменной xi (i=1…n). Применяя теорему разложения, получим

i=0

где fi - значение логической функции на i -ом входном наборе аргументов;

mi - i -ый минтерм или i -ая элементарная конъюнкция максимального ранга.

Из (6.31) следует, что СДНФ логической функции — это дизъюнкция конституент единицы (минтермов), соответствующих наборам входных переменных, для которых функция равна единице. Совершенная дизъюнктивная нормальная форма записывается для истинного значения логической функции. В то же время относительно логической функции можно сказать, что она истинна тогда, когда не ложна. Такое утверждение можно формализовать следующим образом:

87

i=0

где fi - значение логической функции на i -ом входном наборе аргументов;

Mi - i -ый макстерм или i -ая элементарная дизъюнкция максимального ранга.

Представление логической функции в виде(6.33) называется совершенной конъюнктивной нормальной формой (СКНФ).

СКНФ логической функции — это конъюнкция конституент нуля (макстермов), соответствующих входным наборам, для которых функция равна нулю.

Рассмотрим алгоритмы перехода от табличного описания логической функции к ее аналитическому описанию (СДНФ, СКНФ).

Алгоритм перехода от таблицы истинности логической функции к ее записи в виде СДНФ:

1)выбрать в таблице истинности такие входные наборы, на которых функции обращается в единицу;

2)по каждому такому набору составить элементарные конъюнкции максимального ранга (минтермы);

3)в минтермы записать не инвертированными переменные, заданные единицей в таблице истинности, а инвертированными - те переменные, которые в таблице истинности заданы нулем;

4)полученные минтермы соединить между собой знаками дизъюнкции.

Алгоритм перехода от таблицы истинности логической функции к ее записи в виде СКНФ:

88

1)выбрать в таблице истинности такие входные наборы, на которых функция имеет нулевые значения;

2)по каждому такому набору составить элементарные дизъюнкции максимального ранга (макстермы);

3)в макстермы записать не инвертированными переменные, заданные нулем в таблице истинности, а инвертированными - те переменные, которые в таблице истинности заданы единицей;

4)полученные макстермы соединить между собой знаками конъюнкции.

Помимо двух основных (СДНФ и СКНФ) аналитических форм представления функций в алгебре логики существуют дизъюнктивные и конъюнктивные нормальные формы (ДНФ и КНФ), а также минимальные дизъюнктивные

и конъюнктивныенормальныеформы(МДНФи МКНФ). ДНФ/КНФ – это дизъюнкция/конъюнкция элементарных

конъюнкций /дизъюнкций, ранг хотя бы одной из которых отличается от максимального ранга.ДНФ/КНФ называется минимальной, если она содержит наименьшее число букв по сравнению со всеми ДНФ/КНФ, существующими для данной функции. При помощи правил развертывания элементарных конъюнкций и дизъюнкций, ДНФ и КНФ могут быть преобразованы в СДНФ и СКНФ.

В общем виде СДНФ и СКНФ записываются выражениями (6.32) и (6.33), которые могут быть слишком громоздкими. Для их упрощения используется более компактная числовая форма записи, предусматривающая только перечисление десятичных эквивалентов двоичных наборов, на которых функция принимает значение единицы (для СДНФ) или нуля (для СКНФ), соединив их знаками дизъюнкции (для СДНФ) и конъюнкции (для СКНФ).

Пример 6.4. Пусть логическая функция P(x,y,z) задана следующей таблицей истинности (табл. 6.3). Требуется представить ее в виде СДНФ и СКНФ.

89

Решение. По таблице истинности находим, что функция P(x,y,z) принимает единичные значения на четырех входных наборах аргументов. Данным наборам аргументов соответствуют следующие четыре минтерма: xyz , xyz , xyz , xyz .

Тогда, в виде СДНФ данная логическая функция будет представлена в следующем виде:

PСДНФ(x, y, z) = xyz + xyz + xyz + xyz

По аналогии, представим данную логическую функцию в виде СКНФ. В итоге получим:

PСКНФ (x, y, z) =(x + y + z)(x + y + z)(x + y + z)(x + y + z)

(a1 a2.... an) переменных логической функции можно рассматривать как n-мерный вектор, определяющий точку n-мерного пространства. Исходя из этого, всё множество наборов, на которых определена функция n переменных, представляется в видe вершин n-мерного куба. Отмечая точками вершины, в которых функция имеет единичные значения, получают ее гео-

90

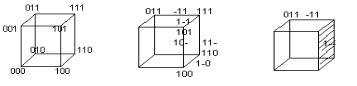
метрическое представление, например так, как показано на рис. 6.7, а.

а) б ) в)

Рис. 6.7. Геометрическое и кубическое представление функции

Y= (3,4,5.6, 7): a — 0-кубы; б — 1-кубы; в — 2-куб

На основе геометрических представлений строятся кубические представления логических функций, в которых используются элементы n-мерных кубов. Геометрически каждому набору (a1 a2.... an) соответствует вершина n-мерного куба с данными координатами. Каждую вершину, на которой функция принимает единичное значение, принято называть 0- кубом (нулевым кубом). Множество 0-кубов образует нулевой кубический комплекс Ко. Например, для функции Y = V(3, 4, 5, 6, 7) нулевой кубический комплекс имеет вид Ко = (011, 100 101, 110, 111) и в данном случае состоит из пяти 0-кубов, каждый из которых соответствует определенной вершине трехмерного куба (рис. 6.7, а).

Если два 0-куба из комплекса К0 различаются только по одной координате, то они образуют один 1-куб (единичный куб). Он представляется общими элементами 0-кубoв, а на месте координаты, по которой различаются 0-кубы, указывается символ «-», обозначающий независимую координату. Например, два 0-куба: 100, 101 различаются только по третьей координате и, следовательно, образуют единичный куб 10-, которому соответствует ребро трехмерного куба. Все множество единичных кубов функции образует единичный кубический комплекс К1. Для функции Y =V(3, 4, 5, 6, 7) он состоит из

91