
524
.pdf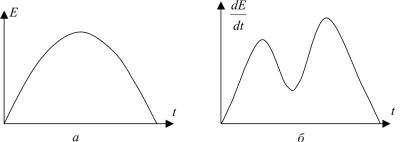
Кратко рассмотрим процесс возбуждения мышечной ткани сердца, или фазу деполяризации [2]. В равновесии любая клетка мышечной ткани поляризована. Внутренняя сторона мембраны клетки заряжена отрицательно, внешняя – положительно. В результате электрического сигнала, генерируемого синусовым узлом, проницаемость мембраны клетки для ионов увеличивается и клетка деполяризуется. Клетки на фазе деполяризации, находящиеся на фронте возбуждения, представляют собой диполи. Сердце с точки зрения формирования в нем электрического потенциала на фазе возбуждения представляет собой один суммарный диполь, величина и направление которого определяются суммой дипольных моментов клеток миокарда, находящихся на линии фронта возбуждения.
Изменение потенциалов сердца приводит к изменению потенциалов на поверхности тела человека, которые регистрируются методами ЭКГ или ВКГ. Особенность метода ВКГ в том, что разности потенциалов регистрируются в трех взаимно перпендикулярных направлениях через очень короткие промежутки времени порядка ~ 0,008 с. В результате удается определить зависимость величины и направления суммарной ЭДС сердца от времени за промежуток, составляющий всего ~ 0,1 с, соответствующий фазе возбуждения.
Рис. 1. Зависимости ЭДС сердца (а) и ее производной (б) от времени на фазе возбуждения
На рис. 1 схематично представлены примеры характерных графиков зависимости величины суммарной ЭДС (Е) и скорости ее изменения (ее производной) от времени [3]. Максимум на кривой (см. рис. 1, а) объяснить легко. Он соответствует моменту времени (примерно равному половине периода возбуждения), когда протяженность фронта возбуждения наибольшая. В этот момент производная ЭДС очевидно близка к нулю, т.е. имеет минимум. Однако не ясно, почему измерения производной ЭДС для всех индивидуумов показывают два максимума за период возбуждения. Это можно было бы объяснить, например, последовательным возбуждением левого и правого желу-
21
дочков. Но возбуждение в правом отделе сердца начинается на ~ 0,01 с раньше, тогда как средний временной интервал между максимумами составляет ~ 0,05 с. В данной работе показано, что вид кривой на рис. 1, а может быть просто связан с геометрической формой поверхности, по которой распространяется фронт возбуждения, а также с тем фактом, что отдельные ЭДС, создаваемые каждой клеткой, следует суммировать векторно.
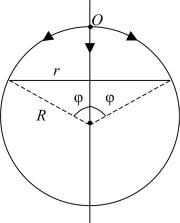
Представим упрощенную модель явления. Рассмотрим распространение процесса возбуждения клеток по однородной сферической поверхности радиусом R. Источник возбуждения – точка О (рис. 2). Тогда фронт возбуждения в каждый момент времени будет представлять собой окружность некоторым радиусом r, диаметр которой виден под углом 2φ из центра сферы. Будем кратко говорить, что фронт возмущения прошел угол φ.
В реальном эксперименте расстояние от источника, т.е. фронта возбуждения, до точек, где измеряются потенциалы, в несколько раз превышает размеры самого фронта возбуждения. Сделаем предположение, существенно упрощающее расчеты, но не влияющее на смысл основных выводов работы. Положим, что расстояние до точек, где измеряются потенциалы, существенно превышает радиус сферы, являющейся источником электрического поля. В этом случае суммарный потенциал, возни-
кающий в некоторой точке пространства, пропорционален суммарному дипольному моменту, а следовательно, и ЭДС, возникающая между какими-либо двумя точками, также пропорциональна суммарному дипольному моменту.
Суммарный дипольный момент в каждый момент времени будет направлен вдоль оси y, перпендикулярной плоскости окружности-фронта, поскольку он складывается из отдельных дипольных моментов, расположенных на этой окружности и направленных по касательной
ксфере. Найдем зависимость величины суммарного дипольного момента Р
искорости его изменения от угла φ.
Пусть n – линейная концентрация отдельных диполей (поляризованных клеток), p0 – величина дипольного момента одной клетки. Тогда проекция дипольного момента каждой клетки на ось y будет равна р0sinφ, а величина суммарного дипольного момента
22
|
|
|
|
P = n 2πr p0 sin ϕ. |
(1) |
||||
|
Пусть ω – угловая скорость распространения фронта возбуждения, |
||||||||
тогда ϕ = ω t . С учетом того, что r = Rsin ϕ, из (1) получаем: |
|
|
|
|
|||||
|
|
|
|
P = n 2πR p sin2 (ω t ) . |
(2) |
||||
|
|
|
|
0 |
|
|
|
|
|
|
Скорость изменения дипольного момента |
|
|
|
|
||||
|
|
dP = n 2πR p ω sin (2ω t ) = n 2πR p ωsin 2ϕ. |
(3) |
||||||
|
|
|
dt |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, за полное время возмущения, когда угол φ принимает |
||||||||
значения от 0 до π, модуль скорости изменения дипольного момента |
|
dP |
|
|
|||||
|
|
||||||||
|
|
|
|
|
|
|
dt |
|
|
(а значит, и скорость изменения ЭДС) |
дважды достигнет максимума при |
||||||||
ϕ = π |
и ϕ = |
3π |
, между которыми будет наблюдаться минимум при ϕ = π . |
||||||
|
|||||||||
4 |
4 |
|
|
|
2 |
|
|
||
Уравнения (2) и (3) согласуются с графиками, представленными на рис. 1. Итак, на примере простой модели, отражающей реальные процессы
фазы возбуждения сердечного цикла, показано, что два максимума графика зависимости модуля скорости изменения суммарной ЭДС от времени могут быть обусловлены исключительно геометрией распространения фронта возмущения.
Список литературы
1.Модифицированный вариант векторкардиограммы в оценке структуры миокарда / Е.Н. Бурдина [и др.] // Нижегородский медицинский журнал. – 2007. – № 6. – С. 193–196.
2.Мир биологии и медицины. Новые методы электрокардиографии / под ред. С.В. Грачева, Г.Г. Иванова, А.Л. Сыркина. – М.: Техносфера, 2007. – 150 с.
3.Бакуцкий В.Н. Пространственная векторэлектрокардиография / В.Н. Бакуцкий, А.Н. Волобуев, Н.Н. Крюков // Кардиология. – 2003. – № 4. –
С. 52–54.
Получено 01.06.2008.
23
УДК 532.5.013.4; 536.25; 534.23
Е.В. Варушкина, А.В. Перминов
Пермский государственный технический университет
ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ВИБРАЦИОННОГО КОНВЕКТИВНОГО ТЕЧЕНИЯ В ПЛОСКОМ СЛОЕ
Рассматривается воздействие слабых акустических вибраций на конвективное движение жидкости в горизонтальном слое, находящемся вполе тяжести. Исследования проводились для вертикальных вибраций, задача решалась в двумерной постановке. В ходе работы было показано, что квазиравновесие для данной системы невозможно, аналитически был получен вид адвективного течения. Далее исследовалась его устойчивость по отношению к малым возмущениям. Без учета сжимаемости повышение вибрационного воздействия приводит к стабилизации течения. При учете сжимаемости в области больших чисел Прандтля наблюдается некоторое уменьшениепорогаустойчивости.
В современной научной литературе большое количество работ посвящено изучению конвективных движений жидкостей под воздействием разного рода вибраций. Как правило, авторы при описании термовибрационной конвекции используют уравнения Зеньковской – Симоненко, где принимаются неакустические приближения, т.е. жидкость считается несжимаемой [1]. Влияние акустических вибраций на конвективное движение жидкости является малоизученным. Впервые уравнения термоакустики были получены Д.В. Любимовым [2, 3]. В данной работе рассматривается влияние эффекта сжимаемости жидкости на устойчивость адвективного течения в плоском слое в условиях микрогравитации. Данная тема представляется интересной в связи с проведением некоторых космических экспериментов, так как в условиях микрогравитации во многие процессы вносят вклад незначительные в земных условиях факторы, в том числе исжимаемость.
Рассмотрим бесконечный слой жидкости толщиной H между двумя горизонтальными пластинами, находящийся в поле тяжести. Жидкость считается сжимаемой. Полость вместе с жидкостью совершает вертикальные вибрации с частотой w и амплитудой b. Пластины считаются идеально теплопроводными. На бесконечности поддерживается постоянный градиент температуры Θ. Рассматривается двумерная постановка, ось x находится
24

в горизонтальной плоскости и сонаправлена градиенту температуры, ось z направлена вертикально вверх. Задача решается в приближении слабой акустики, т.е. длина акустической волны, возбуждаемой в полости, полагается больше ее линейных размеров:
wH 2 |
|
||||
k = |
|
|
<<1. |
(1) |
|
c |
|||||
|
|
|
|
||
Амплитуду пульсационной скорости в данном случае можно представить в виде линейной комбинации акустической и термовибрационной состав-
ляющих: VG =VGa +VGT .
При указанных условиях нагрева и вибраций на фоне пульсационного
движения в жидкости возбуждается осредненное конвективное течение. |
||||||||||||||||||||
Безразмерные уравнения для осредненного поля скорости uG |
и |
поля |
||||||||||||||||||
температуры Т имеют вид: |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
ut +( |
|
) |
|
+ 1 GV a z (z −1) T − |
1 GV t (n VT ) T = − p + ∆ |
|
+GrT |
|
, |
|
|||||||||
|
u |
u |
u |
j |
|
|||||||||||||||
4 |
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
T + |
u |
T = |
∆T , |
|
|
(2) |
|||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
t |
|
Pr |
|
|
|
|
|
||||||
|
|
|
|
|
div |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
u |
= 0, divVT |
= 0, |
rotVT = T ×n, |
|
|
|
|||||||||
где u , VT – скорости осредненного и пульсационного движений жидкости соответственно; n – единичный вектор, направленный вдоль оси вибрации; j – единичный вектор для подъемной силы; p – давление. Задача
характеризуется четырьмя безразмерными параметрами: акустическим, термовибрационным и гравитационным числами Грасгофа:
Gv = gβΘH 3 ν2 , Gv = b2w2β2Θ2H 2 |
ν2 , Gv = b2w4βΘH 4 |
(1− B) ν2c2 |
, |
T |
a |
|
|
и числом Прандтля Pr = ν/ χ . |
|
|
|
Так как ось вибраций совпадает с осью z, то
n VT =VT z .
Граничные условия:
z = 0, 1: u = 0, VT z = 0, T = x.
Кроме того, справедливо условие замкнутости течения вдоль оси x:
∫1 VT xdz = 0, ∫1 uxdz = 0.
0 0
25

Для данной системы первоначально исследовалась возможность квазиравновесного состояния. Хорошо известно, что несжимаемая жидкость в подобной системе может находиться в квазиравновесии. Автором было показано, что при учете сжимаемости это невозможно.
Далее исследуется адвективное течение жидкости, т.е. течение в горизонтально ориентированной полости при горизонтальном градиенте температуры. Поскольку слой бесконечный, то скорость жидкости не зависит от x:
u = {ux (z),0,0} .
Так как рассматривается установившееся течение, то все производные по времени зануляются:
ut = 0, Tt = 0.
Границы полости считаются идеально теплопроводными, тогда в центре полости должно выполняться:
T = x + ϑ(z).
Для данной постановки с использованием уравнений (2) было получено следующее решение:
|
|
|
|
|
z |
4 |
|
|
|
z |
3 |
|
|
|
z |
2 |
|
|
|
|
|
z |
|
|
|
|
|
z |
3 |
|
|
z |
2 |
|
|
|
|
z |
|
|
|
|
|
|
|
|
|||||
ux |
= GV a |
|
|
|
− |
|
|
|
+ |
|
|
− |
|
|
|
|
|
+ Gr |
|
|
− |
|
+ |
|
|
|
, |
|
|
|
|
|
|||||||||||||||||||
48 |
|
24 |
40 |
240 |
6 |
|
|
12 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
z |
6 |
|
|
|
|
z |
5 |
|
|
|
|
|
z |
4 |
|
|
|
|
|
z |
3 |
|
|
|
|
|
|
|
z |
5 |
|
|
|
|
z |
4 |
|
|
|
z |
3 |
|
z |
|
|
|||
T = x + Pr GV a |
|
|
|
|
− |
|
|
|
+ |
|
|
|
|
− |
|
|
|
|
|
|
+ Gr |
|
|
|
|
− |
|
|
+ |
|
|
− |
|
, |
|||||||||||||||||
1440 |
|
480 |
|
|
480 |
1440 |
|
120 |
|
|
|
72 |
720 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
48 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
V |
|
= z − 1 |
, V |
|
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
T x |
|
|
|
|
|
2 |
|
|
T z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для наглядности приведем несколько профилей ux и T . Наибольший интерес представляет исследование влияния акустической составляющей скорости на течение жидкости, поэтому ограничимся малым параметром Gr .
Рассматривается случай Pr = 1 (газ). Профильтемпературыстроитсяпри x = 0. В случае отсутствия гравитационного поля в полости под действием акустических вибраций возникает возвратное течение, интенсивность которого по мере роста GV a возрастает (рис. 1). Профили скорости
и температуры являются четными функциями.
26
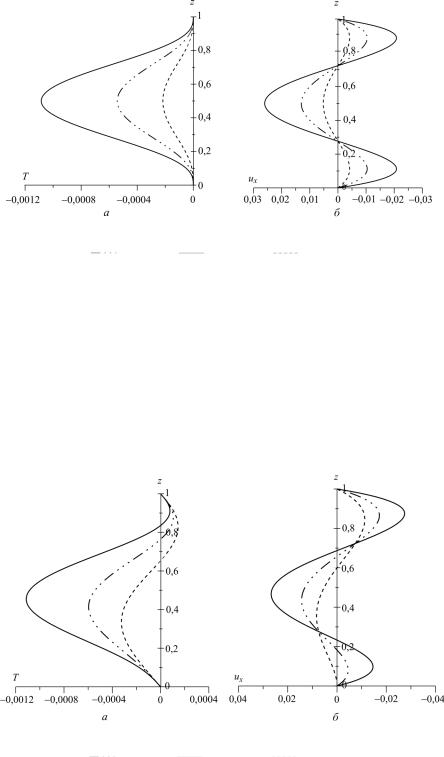
Рис. 1. Профили температуры (а) и скорости (б) при Gr = 0:
GV a = 50; |
GV a = 100; GV a = 20 |
При Gr = 1 профили ux и T |
теряют симметрию, можно наблюдать |
борьбу конвективного и термоакустического течений, возвратное течение возникает, но развивается медленно (рис. 2).
При Gr = 100 гравитационный механизм генерации течения сводит
к минимуму эффекты, обусловленные сжимаемостью жидкости.
Таким образом, полученные результаты согласуются с практикой, т.е. учет сжимаемости жидкости при сильном гравитационном поле нецелесообразен. Также показано, что в слабом гравитационном поле сжимаемостью жидкости нельзя пренебрегать, так как она оказывает существенное влияние на вид течения.
Рис. 2. Профили температуры (а) и скорости (б) при Gr = 1:
GV a = 50; GV a = 100; GV a = 20
27

Исследуем устойчивость данного решения. Для этого внесем малые возмущения в следующие поля:
u = u0 +u′, VT =V0 +V ′, T =T0 +T′, p = p0 + p′,
где штрих означает некоторое возмущение исходного решения. Подставим данные выражения в исходную задачу, оставляя только линейные по возмущениям члены:
u′+(u0 )u′+(u′ )u0 + 14 GV a z (z −1) T′− 12 GV T Vz′ T0 = − p′+ ∆u′+GrT′j , Tt′+u′ T0 +u0 T′ = Pr1 ∆T′,
divu′ = 0, divV ′ = 0, rotV ′ = T′×n.
Граничные условия для возмущений возьмем в следующем виде: z = 0,1: u′ = 0, V ′ = 0, T′ = 0.
Рассмотрим устойчивость адвективного течения относительно плоских возмущений, т.е. возмущений в виде валов с осями, перпендикулярными вектору скорости основного потока:
(u′,V ′, p′,T′) = (u ,V , p,T )(z)e−ikx+λt .
Теперь задачу можно свести к уравнениям относительно амплитуд возмущений:
ϕ|V = (λ+ 2k2 −ik u0 )ϕ′′+(u0′′+ k 2u0 − k2λ − k4 )ϕ−
|
1 |
|
|
|
1 |
GV T |
′ |
′ ′ |
|
|
− ik |
4 |
GV a (2z −1) +Gr T − |
2 |
(Vz |
+ikVzϑ0 ), |
|||||
|
|
|
|
|
|
|
|
|||
T |
′′ |
= (k |
2 |
|
|
|
′ |
′ |
, |
|
|
|
+ Pr (λ −iku0 ))T + Pr ϕ +ik Pr ϕϑ0 |
||||||||
Vz′′= k2Vz −k 2T ,
где функция тока (точнее, здесь записана ее амплитуда) вводится следующим образом:
′ |
= ikϕ. |
ux = ϕ , uz |
Граничные условия для амплитуд перепишутся в виде:
z = 0, 1: ϕ = ϕ′ = 0, Vz = 0, T = 0.
28
Данная задача решалась численно с помощью метода дифференциальной прогонки с процедурой стыковки в промежуточной точке z = 0,5 .
Перейдем к обсуждению результатов решения задачи. Исследования проводились для большого класса жидкостей с числами Прандтля от 0,01 (жидкие металлы) до 6,7 (вода). Ниже приводятся графики зависимости критических чисел Грасгофа от чисел Прандтля. Под критическими здесь понимаются минимизированные по волновому числу значения.
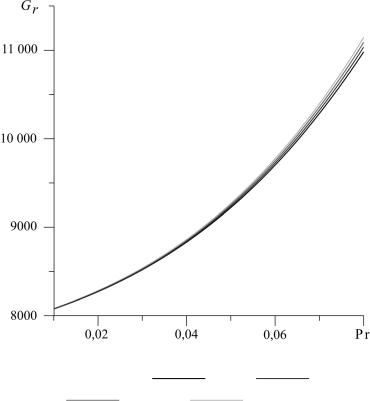
На рис. 3, 4 нижний график повторяет известный результат из работы [4], на рис. 3 представлена так называемая гидродинамическая мода, на рис. 4 – рэлеевская мода. В ходе работы был получен эффект повышения устойчивости течения при увеличении термовибрационного параметра. Это должно означать, что при увеличении амплитуды или частоты вибраций повышается порог устойчивости. Однако дальнейшие исследования показали, что при учете сжимаемости это не совсем так. Для расчета была выбрана верхняя кривая (см. рис. 3, 4) (при GV T = 1500 ).
Результат показан на рис. 5.
Рис. 3. Зависимости критических чисел Грасгофа от чисел Прандтля. Гидродинамическая мода: GV t = 0; GV t = 500;
GV t = 1000; GV t = 1500
29
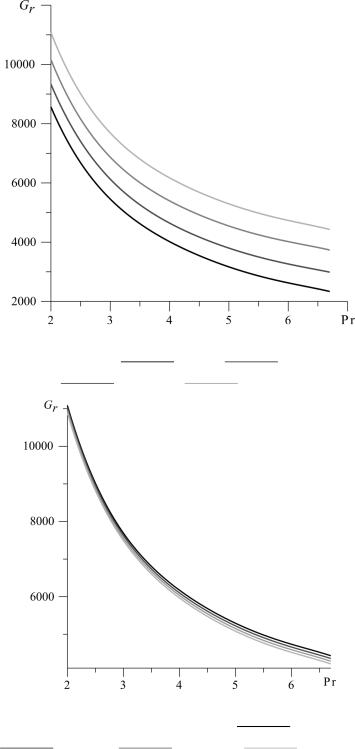
Рис. 4. Зависимости критических чисел Грасгофа от чисел Прандтля. Рэлеевская мода: GV t = 0; GV t = 500;
GV t = 1000; GV t = 1500
Рис. 5. Зависимости критических чисел Грасгофа от чисел Прандтля. Рэлеевская мода (учет сжимаемости): GV а = 0;
GV а = 500; GV а = 1000; GV а = 1500
30
