524

Важными параметрами процесса фильтрации жидкости в пористой среде являются коэффициент сопротивления k и пористость данной среды

– разность текущего и начального значений высоты столба жидкости над поверхностью почвы; ∆l – разность текущего и начального значений глубины проникновения раствора в почве. В таблице показаны средние значения пористости почвы для каждого отдельного эксперимента αср .

Эксперимент по очистке почвы от тяжелых металлов проводился в стеклянных колонках: изучалась динамика проникновения водного раствора биосурфактанта. В отличие от эксперимента по очистке нефтезагрязненного грунта в данном эксперименте наблюдалось прохождение всех порций биосурфактанта с равной скоростью. Таким образом, предполагаем, что в данной задаче жидкость течет под действием силы тяжести и объемной силы сопротивления, пропорциональной скорости; т.е. постановку задачи (1) модифицируем с учетом эксперимента:

Данное уравнение интегрировали с учетом дополнительных условий

(4). При этом учитывали, что в ходе эксперимента жидкость заливали на заданную величину h0 и после не доливали. В момент, когда h0 = 0, жидкость снова заливали на заданную величину h0 и после не доливали. Тогда для h(t) выразим следующим образом:

111

В данном решении неизвестным является параметр k, который находили с помощью обработки экспериментальных данных методом наименьших квадратов.

Средние значения пористости почвы

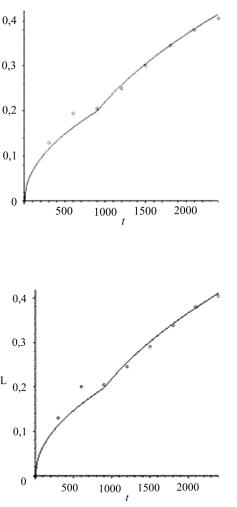
Рис 4. Экспериментальная и теоретическая зависимости глубины проникновения растворов солей никеля от времени

Рис 5. Экспериментальная и теоретическая зависимости глубины проникновения растворов солей молибдена от времени

112

Экспериментальная и теоретическая зависимости глубины проникновения растворов солей никеля и молибдена от времени представлены на рис. 4, 5.

Список литературы

1.Ившина И.Б. Применение экологически безопасной экспресстехнологии очистки нефтезагрязненных почв и грунтов / И.Б. Ившина, М.С. Куюкина, С.М. Костарев // Нефтяное хозяйство. – 2003. – № 9. –

С. 116–118.

2.Mathematical modelling of crude oil-contaminated soil washing process using Rhodococcus-biosurfactant / M.S. Kuyukina [et al.] // Environmental Modelling and Simulation: Proc. Third IASTED Int. Conference. Honolulu. (USA), 2007. – P. 77–81.

3.Костина Л.В. Десорбция молибдена из почвы под действием биогенных и синтетических сурфактантов / Л.В. Костина [и др.] // Проблемы загрязнения окружающей среды: матер. VI Междунар. конф. – Пермь;

Казань, 2005. – С. 34.

Получено 15.09.2008.

113

УДК 517.977

С.Ю. Култышев, Л.М. Култышева

Пермский государственный технический университет

ИДЕНТИФИКАЦИЯ ЛИНЕЙНЫХ СТОХАСТИЧЕСКИХ МОДЕЛЕЙ РЕАЛЬНЫХ ОБЪЕКТОВ

Рассматривается задача нахождения параметров линейной стохастической модели реального объекта по измерениям его входа и выхода. Получены теоремы, дающие решение этой задачи для указанной модели при некоторых видах измерений входа и выхода объекта.

Пусть Rn – пространство n-мерных векторов, компонентами которых являются действительные числа; B1m[θ,T ] и B2n[θ,T ] – нормированные пространства m- и n-мерных вектор-функций, определенных на отрезке [θ,T ] R1 ; Y , Z и W – нормированные пространства.

Рассмотрим реальный объект на отрезке времени [θ,T ], где θ – момент возникновения объекта. Через V (t) обозначим вектор параметров,

некоторые из внешних воздействий имеют случайный характер, то можно

известном V, где V и X – входной и выходной случайные процессы.

114

имеет в области Ω единственное решение ω, то задача идентификации для (1),(2),(3) имеет единственное решение ω = ω.

115

Доказательство. Поскольку стохастическая модель объекта имеет вид (1),

тельно, ω удовлетворяет уравнению (4). Но уравнение (4) имеет единственное

образом, мы нашли ω = ω, при котором (1) является стохастической моделью объекта, причем оно единственно, так как уравнение (4) имеет единственное решение ω = ω. Следовательно, задача идентификации для (1), (2), (3) имеет единственноерешение ω = ω. Теоремадоказана.

Эту теорему иллюстрирует пример 1. Рассмотрим электрическую цепь из последовательно соединенных индуктивности L и активного сопротивления R . Через V (t) обозначим напряжение на входе цепи, а через

X (t) – выходной ток в цепи. Пусть θ = 0, T = 3 . Стохастическая модель этой цепи имеет вид

функций с производной из L11[0;3], V (t) – гауссовский случайный процесс

116

математическим ожиданием.

Стохастическую модель (5) можно записать в эквивалентном интегральном виде:

117

Далее пусть стохастическая модель объекта имеет вид (1), а измерения входа и выхода объекта имеют вид

где Q :W → Rk – линейный ограниченный оператор.

имеет в области Ω единственное решение ω, то задача идентификации для (1), (9) имеет единственное решение ω = ω.

Доказательство. Поскольку стохастическая модель объекта имеет вид (1),

Но это уравнение имеет единственное решение ω в области Ω , следовательно, ω = ω и задача идентификации для (1), (9) имеет единственное решение ω = ω. Теорема доказана.

118

Эту теорему иллюстрирует пример 2. Рассмотрим электрическую цепь из примера 1 в тех же предположениях, тогда стохастическая модель этой цепи имеет вид (6). Пусть измерения входа и выхода этой цепи имеют

t [0;3],vp и xp – реализации случайных процессов V и X . Модель (6) можно записать в виде (1), если положить α1 (ω) = RL , β1(ω) = L1 . Тогда уравнение (10)

имеет вид RL z1 + L1 y1 = z0 или(что то же самое)

Работа выполнена при финансовой поддержке РФФИ (проекты № 06- 01-00744 и № 07-01-96060).

Получено 15.09.2008.

119

УДК 531/534: [57+61]

И.В. Кушнирева, К.В. Подъянова, Н.С. Шабрыкина

Пермский государственный технический университет

СТАЦИОНАРНАЯ МОДЕЛЬ ТЕЧЕНИЯ ИНТЕРСТИЦИАЛЬНОЙ ЖИДКОСТИ В ТКАНЕВОЙ ОБЛАСТИ

Данная работа посвящена математическому моделированию обменных процессов, происходящих в тканевой области. Целью построения данной модели является выявление причин расстройств функционирования микроциркуляторного русла.

Ткань моделируется как пороупругая среда, считается изотропной и подчиняется линейным определяющим соотношениям теории упругости. Рассматривается конечная тканевая область, окружающая одиночный кровеносный капилляр. Течение жидкости через стенку капилляра подчиняется закону Старлинга.

В данной работе решалась задача Лапласа для области вне цилиндра с граничными условиями второго и третьего рода. В результате решения этой задачи методами математической физики получено распределение давления тканевой жидкости в аксиальном и радиальном направлениях. Закон Дарси позволяет найти распределение скоростей течения жидкости в тканевой области, а также объемную скорость фильтрации, что дает возможность сделать количественную оценку обменных процессов, происходящих в микроциркуляторном русле.

Введение

Организм человека представляет собой сложную биологическую систему, в которой непрерывно происходят физические и химические процессы. Одним из основных является обмен веществ, так как главные его задачи заключаются в обеспечении питания и удалении продуктов метаболита каждой клетки в отдельности. Обмен веществ между кровью и клетками ткани происходит на уровне микроциркуляторного русла, где жидкость и растворенные в ней вещества, а также частично макромолекулы переходят сквозь полупроницаемую стенку кровеносного капилляра в интерстициальное пространство, где происходит обмен веществ с клетками ткани. Затем жидкость частично всасывается обратно в кровеносное русло, частично – в лимфатические капилляры [1].

120