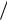2713
.pdf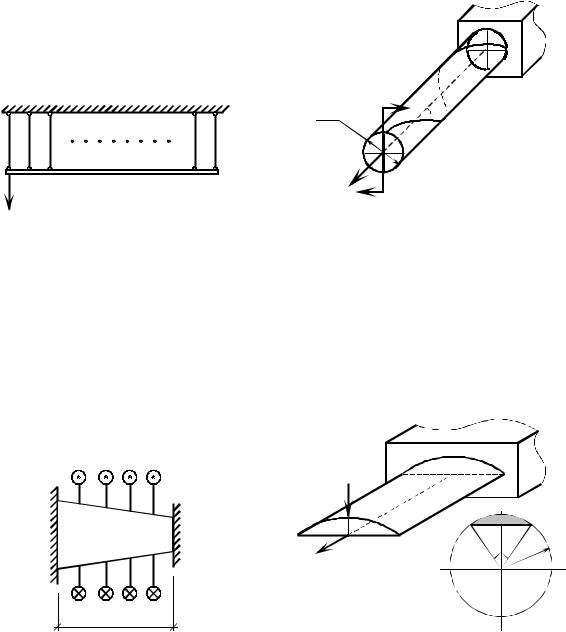
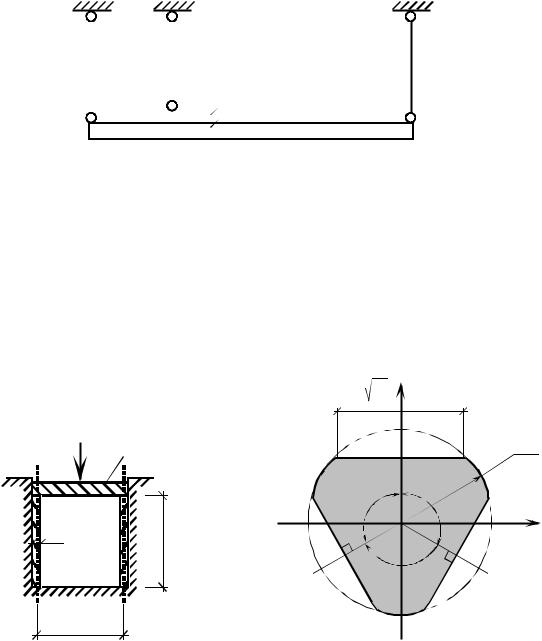
10.120. Абсолютно жесткий брус подвешен на трех стержнях.
Второй стержень имеет монтажный натяг (рис. 10.120). Как нужно изменить температуру первого стержня после сборки системы, чтобы брус принял горизонтальное положение?
1 |
|
2 |
|
|
|
|
|
3 |
|
l, A |
|
|
l, A |
|
|
l, A |
|
|
|
a |
|
|
|
|
|
3a |
|
|
|
||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Рис. 10.120
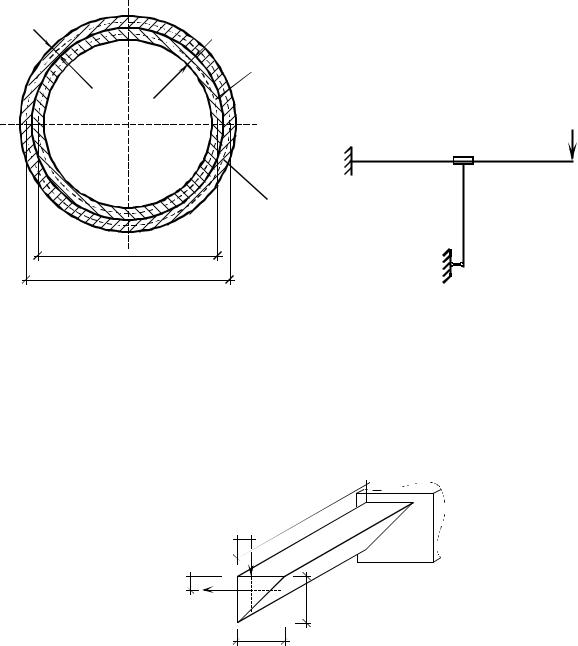
10.121. Трубка длиной l, толщиной и средним диаметром D 20 вставляется без зазора и натяга в абсолютно жесткий и гладкий канал и нагружается через жесткий плунжер сжимающей силой F (рис. 10.121). Определить силу F, при которой изменение длины трубки будет равно l , если коэффициент Пуассона 0,3.
10.122. Определить осевые моменты сопротивления Wx и Wy данной плоской фигуры (рис. 10.122).
|
R |
2 |
y |
|
F Плунжер |
|
R |
|
120O |
120O |
|
|
|
|
x |
l |
|
|
|
|
|
|
|
|
|
120O |
|
|
D |
|
|
Рис. 10.121 |
Рис. 10.122 |
||
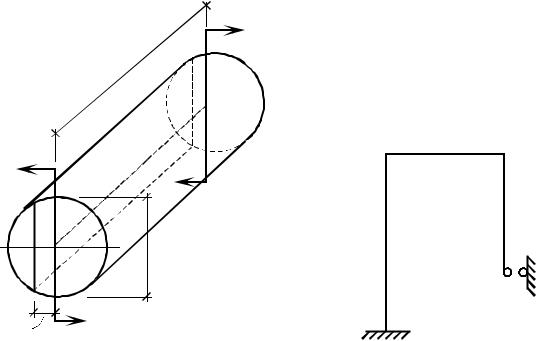
10.123. Круглый брус диаметром d и длиной l скручивается моментами T (рис. 10.123). Определить момент M от касательных напряжений, возникающий в продольных сечениях бруса, отстоящих от оси на расстоянии d / 4, если l 10d .
123

ОТВЕТЫ И УКАЗАНИЯ
К главе 1
1.1. arctg(
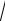 2 / 2).
2 / 2).
1.2. = 45 . 1.3. = 90 – .
1.4. sin 2 cos sin 2( ) 0.
1.5. Окружность радиуса EAPl .
1.6. А = 2,3 см2.
1.7. ЕВС = 105 МПа, ЕBD = 2 105 МПа.
1.8. |
|
1 |
|
|
|
2 |
|
|
|
||
|
|
arctg |
|
|
|
. |
|
|
|||
2 |
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1.9. |
|
|
|
3 |
|
, |
vB |
3Pl |
. |
||
arctg |
|
|
|
||||||||
4 |
EAsin |
||||||||||
|
|
|
|
|
|
|
|
|
|||
1.10.= 45 .
1.11.= 45 , может быть любым.
1.12.Р = 6403 кН.
1.13.= 45 .
1.14.= 90 .
1.15. cos2 |
|
|
n |
|
. |
|
|
|
|
|
|||
2n 1 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||
1.16. Ñ |
6Pl |
. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
EA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3P |
|
|
|
|||
1.17. 0 1 |
|
, где 0 |
|
|
|
. |
|
||||||
5 r |
2 |
|
|||||||||||
|
|
|
|
|
r |
|
|
|
|
|
|||
1.18. Эпюра N – прямая с ординатами –Р на левом и +2Р на пра- |
|||||||||||||
вом конце. l |
Pa |
. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
|
|
2EA |
|
|
P A на конце ленты и |
|
|||||||
1.19. Прямая с ординатами |
0 в |
||||||||||||
точке, отстоящей на расстоянии P qf от конца. |
|
||||||||||||
1.20. l1 l2 1. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
125 |
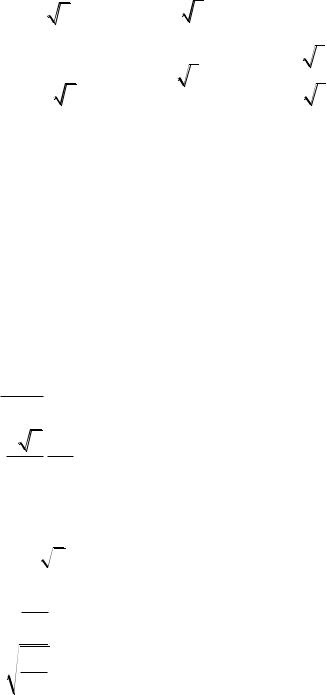
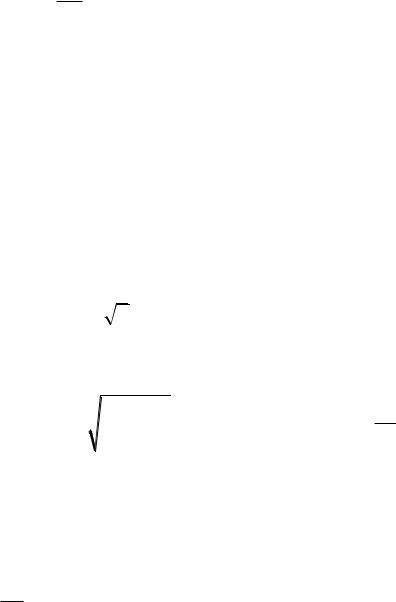
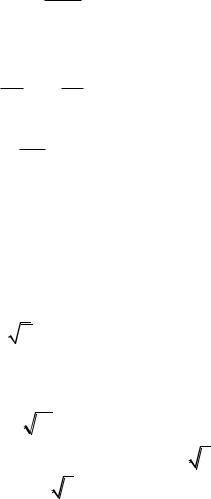
2.38. Указание: использовать выражение объемного закона Гука.
2.39. A 1 klT .
2E
2.40. V 1 2 18a2tp .
E
2.41. max = 100 МПа, = 30 .
К главе 3
3.1. Указание: учесть, что центр тяжести всей фигуры лежит на прямой, соединяющей центры тяжести двух составляющих фигур.
3.2. Так как фигура состоит из двух одинаковых составных частей, повернутых относительно друг друга на 90 , одна из главных осей – линия, соединяющая два центра тяжести.
3.3. См. ответ к задаче 3.2.
3.4. h H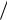 2. 3.5. Iz bh3
2. 3.5. Iz bh3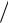 3.
3.
3.6. Iz2 0,91a4. 3.7. I = 2 688 cм4.
3.8. Iz1 |
|
|
1 |
|
a4 |
|
|
d 4 |
|
|
|
|
|
|||||||
|
2 |
|
|
12 |
|
64 |
. |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3.9. Iz y |
|
336 a4 . |
|
|
|
|
|
|
|
|||||||||||
1 |
1 |
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3.10. Iz1 |
|
|
|
|
4a3b3 |
|
|
|
|
b4 |
|
|
||||||||
|
|
|
|
|
|
|
8 . |
|
||||||||||||
3 a2 |
b2 |
|
|
|||||||||||||||||
3.11. Izy |
|
|
|
|
|
|
|
|
a |
|
|
|
d |
|
, где А – площадь всей фигуры. |
|||||
A b |
2 |
c |
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3.12. I |
|
|
|
|
|
1 b3h3 |
|
. |
|
|
|
|
|
|
||||||
I I |
|
48 |
|
m2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3.13. Iz |
1,35r4 . |
|
|
|
|
|
|
|
|
|
||||||||||
3.14. Iz0 |
|
|
|
r |
4 80 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
3 |
|
2 |
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|||||||
129
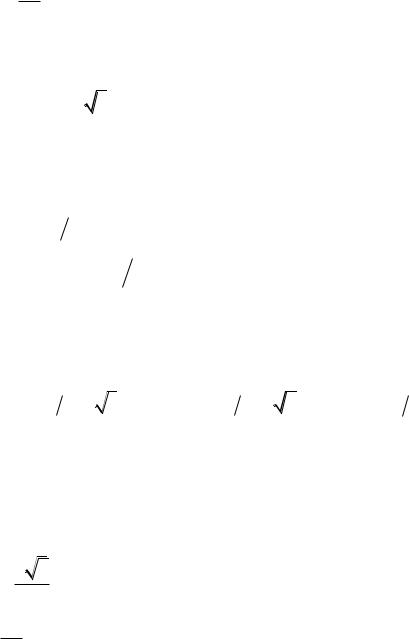

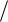 2
2 
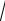 2 0,59
2 0,59
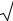 ).
).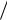 l
l
 3
3 2.
2.