
Электродинамика сплошных сред
..pdfМинистерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования «Пермский национальный исследовательский политехнический университет»
И.В. Колесниченко
ЭЛЕКТРОДИНАМИКА СПЛОШНЫХ СРЕД
Утверждено Редакционно-издательским советом университета
в качестве учебного пособия
Издательство Пермского национального исследовательского
политехнического университета 2013
УДК 537.8 (075.8) К60
Рецензенты:
д-р физ.-мат. наук, профессор Д.Д. Соколов (Научно-исследовательский вычислительный центр МГУ, г. Москва); д-р физ.-мат. наук, профессор Г.Ф. Путин
(Пермский государственный национальный исследовательский университет)
Колесниченко, И.В.
К60 Электродинамика сплошных сред: учеб. пособие / И.В. Колесниченко. – Пермь: Изд-во Перм. нац. исслед. политехн. ун-та, 2013. – 207 с.
ISBN 978-5-398-00984-2
Электродинамика сплошных сред теоретически и экспериментально изучает явления, в которых либо напряжения, деформации или скорости деформации влияют на электрическое и магнитное состояние вещества, либо силы и моменты сил, созданные электромагнитными полями, влияют на механическое состояние вещества. В ходе некоторых, наиболее сложных процессов происходит взаимодействие процессов переноса движущейся средой магнитного поля и воздействия магнитного поля на движущуюся среду. Разделы электродинамики сплошных сред имеют значение не только для фундаментальной, но и для прикладной науки.
Приводятся задания для самостоятельного выполнения и вопросы для самопро-
верки.
Изучение материала, включенного в учебное пособие, предусмотрено в рамках учебного плана профиля магистратуры «Математическое моделирование физикомеханических процессов» по направлению 010400.68 «Прикладная математика и информатика».
УДК 537.8
ISBN 978-5-398-00984-2 |
c |
ПНИПУ, 2013 |
Оглавление
Предисловие . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
7 |
Список обозначений . . . . . . . . . . . . . . . . . . . . . . . . |
10 |
1. Уравнения Максвелла для сплошной среды |
13 |
1.1. Электростатика . . . . . . . . . . . . . . . . . . . . . . . |
14 |
1.1.1.Электрический заряд и электрическое поле . . . . 14
1.1.2.Электростатическое поле в вакууме . . . . . . . . 16
1.1.3. |
Электростатическое поле в проводниках . . . . . |
18 |
1.1.4. |
Потенциал уединенного заряда в плазме . . . . . |
19 |
1.2. Диэлектрики в электрическом поле . . . . . . . . . . . . |
22 |
|
1.2.1. |
Электрические диполи . . . . . . . . . . . . . . . |
22 |
1.2.2. Поляризация диэлектриков . . . . . . . . . . . . . |
24 |
|
1.2.3. |
Поляризация неполярных диэлектриков . . . . . |
25 |
1.2.4.Поляризация полярных диэлектриков . . . . . . . 26
1.2.5.Пондеромоторные силы в диэлектриках . . . . . . 29
1.3. Постоянный электрический ток . . . . . . . . . . . . . . . |
30 |
|
1.3.1. |
Сила и плотность электрического тока . . . . . . |
30 |
1.3.2. |
Законы Ома и Джоуля . . . . . . . . . . . . . . . |
31 |
1.3.3. Электродвижущая сила . . . . . . . . . . . . . . . |
32 |
|
1.3.4. |
Классическая электронная теория электропро- |
|
|
водности проводников . . . . . . . . . . . . . . . . |
33 |
1.3.5.Введение в квантовую электронную теорию электропроводности проводников . . . . . . . . . 36
1.3.6.Полупроводники и электролиты . . . . . . . . . . 39
1.3.7. |
Уравнение непрерывности электрического тока . |
41 |
1.3.8. |
Плотность тока в реальной среде . . . . . . . . . |
42 |
1.4. Магнетизм . . . . . . . . . . . . . . . . . . . . . . . . . . |
44 |
|
3
1.4.1. |
Магнитная индукция и магнитный диполь . . . . . |
44 |
1.4.2. |
Магнитное поле электрического тока . . . . . . . |
45 |
1.4.3.Электромагнитная индукция . . . . . . . . . . . . 48
1.4.4.Самоиндукция . . . . . . . . . . . . . . . . . . . . 49
1.4.5. |
Сила Лоренца . . . . . . . . . . . . . . . . . . . . |
51 |
1.4.6. Поведение движущихся зарядов в магнитном поле |
52 |
|
1.5. Термоэлектромагнитные явления . . . . . . . . . . . . . . |
54 |
|
1.5.1. |
Контактная разность потенциалов . . . . . . . . . |
54 |
1.5.2. |
Эффект Томпсона . . . . . . . . . . . . . . . . . . |
55 |
1.5.3.Эффекты Пельтье и Зеебека . . . . . . . . . . . . 58
1.5.4.Термогальваномагнитные явления . . . . . . . . . 61
1.6. |
Магнетики . . . . . . . . . . . . . . . . . . . . . . . . . . |
62 |
|
|
1.6.1. |
Намагничивание . . . . . . . . . . . . . . . . . . . |
62 |
|
1.6.2. |
Природа молекулярных токов . . . . . . . . . . . |
63 |
|
1.6.3. |
Спин . . . . . . . . . . . . . . . . . . . . . . . . . |
65 |
|
1.6.4. |
Диамагнетизм (µ < 1) . . . . . . . . . . . . . . . . |
66 |
|
1.6.5. |
Парамагнетизм (µ > 1) . . . . . . . . . . . . . . . |
67 |
|
1.6.6. |
Ферромагнетизм (µ 1) . . . . . . . . . . . . . . |
69 |
|
1.6.7. |
Плотность молекулярного тока . . . . . . . . . . |
72 |
|
1.6.8. |
Пондеромоторные силы в магнетиках . . . . . . . |
74 |
1.7. |
Электромагнитное поле в веществе . . . . . . . . . . . . |
74 |
|
|
1.7.1. |
Система уравнений Максвелла . . . . . . . . . . . |
74 |
|
1.7.2. |
Движение проводника в магнитном поле . . . . . |
78 |
|
1.7.3. Уравнение переноса поля . . . . . . . . . . . . . . |
82 |
|
1.8. |
Электромагнитные волны . . . . . . . . . . . . . . . . . . |
83 |
|
1.8.1.Электромагнитные волны в вакууме . . . . . . . . 83
1.8.2.Энергия, давление, импульс и масса
электромагнитного поля . . . . . . . . . . . . . . 86
1.8.3.Электромагнитная масса движущегося заряда . . 88
1.8.4.Монохроматическая волна. Поляризация волны . 90
1.8.5.Электромагнитные волны в реальной среде . . . . 91
1.9. Электромагнитное излучение . . . . . . . . . . . . . . . . |
94 |
|
1.9.1. |
Виды электромагнитного излучения . . . . . . . . |
94 |
1.9.2. |
Эффект Доплера . . . . . . . . . . . . . . . . . . . |
96 |
4
1.9.3. Излучение Вавилова-Черенкова . . . . . . . . . . 98 1.9.4. Переменное электромагнитное поле в проводнике 101
1.9.5.Прохождение электромагнитной волны сквозь диэлектрик . . . . . . . . . . . . . . . . . . . . . . 103
2.Взаимодействие сред с электрическими
и магнитными полями |
108 |
2.1. МГД-течение в плоском слое электропроводящей жид- |
|
кости . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
108 |
2.1.1.Уравнения магнитной гидродинамики . . . . . . . 108
2.1.2.МГД-течения Куэтта и Гартмана . . . . . . . . . . 110
2.1.3.Распределение магнитного поля . . . . . . . . . . 113
2.1.4. |
Гидравлические характеристики течения Гартмана |
115 |
2.2. МГД-канал . . . . . . . . . . . . . . . . . . . . . . . . . . |
117 |
|
2.2.1. |
МГД-канал как кондукционная машина . . . . . |
117 |
2.2.2.Интегральные соотношения для кондукционного МГД-канала . . . . . . . . . . . . . . . . . . . . . 119
2.2.3.Кондукционные МГД-насос и МГД-двигатель . . 121
2.2.4.Кондукционные МГД-вентиль, расходомер и генератор . . . . . . . . . . . . . . . . . . . . . . . . 123
2.2.5.Поведение включения в МГД-канале . . . . . . . 126
2.3. Электромагнитная сила в проводниках . . . . . . . . . . 128
2.3.1.Механизмы генерации электромагнитной силы . . 128
2.3.2.Двумерные уравнения Максвелла . . . . . . . . . 129
2.3.3.Магнитное поле тока при наличии ферромагнетиков131
2.3.4.Переменный ток . . . . . . . . . . . . . . . . . . . 134
2.3.5.Индукционный механизм генерации электромагнитной силы . . . . . . . . . . . . . . . 138
2.3.6.Бегущее магнитное поле над металлическим полупространством . . . . . . . . . . . . . . . . . 140
2.4.Электровихревые течения . . . . . . . . . . . . . . . . . . 144
2.4.1. Генерация ЭВТ . . . . . . . . . . . . . . . . . . . 144
2.4.2.ЭВТ и азимутальное течение . . . . . . . . . . . . 147
2.4.3.ЭВТ в плоском канале со свободной поверхностью 150
5
2.5. Перенос магнитного поля в лабораторных масштабах . . . . . . . . . . . . . . . . . . . . . . . . . . 154
2.5.1.Генерация больших магнитных полей. Гидромагнит Кольма . . . . . . . . . . . . . . . . . . . . . . 154
2.5.2.Сверхпроводники . . . . . . . . . . . . . . . . . . 157
2.5.3.Сверхпроводник в магнитном поле. Квантование магнитного потока . . . . . . . . . . . . . . . . . . 160
2.6.Взаимодействие плазмы с электрическими
и магнитными полями . . . . . . . . . . . . . . . . . . . . |
165 |
|
2.6.1. |
Виды плазмы . . . . . . . . . . . . . . . . . . . . . |
165 |
2.6.2. |
Плазменные волны . . . . . . . . . . . . . . . . . |
169 |
2.6.3.Ускорение плазмы в космическом пространстве . 171
2.6.4.Применение плазмы для производства электроэнергии . . . . . . . . . . . . . . . . . . . . . . . . 174
2.6.5.Равновесие плазмы в магнитном поле . . . . . . . 175
2.6.6. |
Неустойчивости плазмы . . . . . . . . . . . . . . |
178 |
2.6.7. |
Неустойчивости линейного пинча . . . . . . . . . |
181 |
2.6.8. Установки для удержания плазмы . . . . . . . . . 183
2.7.Генерация магнитного поля движущейся
проводящей средой . . . . . . . . . . . . . . . . . . . . . |
186 |
|
2.7.1. Теорема Альфвена . . . . . . . . . . . . . . . . . . |
186 |
|
2.7.2. |
Теорема Валена . . . . . . . . . . . . . . . . . . . |
188 |
2.7.3. |
Волны Альфвена . . . . . . . . . . . . . . . . . . |
189 |
2.7.4.Теорема Каулинга . . . . . . . . . . . . . . . . . . 191
2.7.5.МГД-динамо . . . . . . . . . . . . . . . . . . . . . 193
Предметный указатель . . . . . . . . . . . . . . . . . . . . . . |
197 |
Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . |
200 |
Задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
202 |
Список литературы . . . . . . . . . . . . . . . . . . . . . . . . |
205 |
Предисловие
Электродинамика и механика сплошных сред обычно рассматриваются как два раздела макроскопической физики. Электродинамика – это наука об электрических зарядах, находящихся в движении. Механика сплошных сред – наука о деформациях и течениях в веществе под действием внешних факторов (сил, моментов сил и т.д.). В обоих случаях все переменные величины рассматриваются в виде полей, т.е. достаточно гладких функций координат и времени. Состояние покоя (отсутствие изменения во времени) в обеих дисциплинах рассматривается как частный случай. «Вещество», с которым имеет дело механика сплошных сред, включает составляющие, которые также являются объектом исследования электродинамики, и комбинация этих двух дисциплин рано или поздно должна была возникнуть.
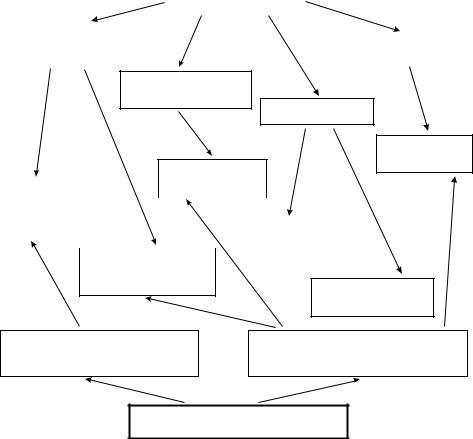
Электродинамика сплошных сред изобилует эффектами, в которых либо напряжения, деформации или скорости деформации влияют на электрическое и магнитное состояние вещества, либо силы и моменты сил, созданные электромагнитными полями, влияют на механическое состояние вещества. Ниже показана схема взаимосвязи разделов, входящих в состав дисциплины «Электродинамика сплошных сред».
Целью изучения данной дисциплины является овладение знаниями физических законов и теорий электродинамики сплошных сред для их эффективного использования при построении математических моделей систем и процессов.
Предметом изучения дисциплины являются следующие объекты: основные понятия и определения электродинамики сплошных сред; физические основы и процессы, используемые в рамках электродинамики сплошных сред; физические законы и теории для описания процессов, изучаемых в рамках электродинамики сплошных сред; современные подходы для описания явлений, изучаемых в рамках электродинамики сплошных сред; фундаментальные процессы, описание которых возможно в рамках электродинамики сплошных сред; технологии инновационного и прикладного направления науки, в которых использованы процессы, изучаемые в курсе электродинамики сплошных сред.
7
В результате освоения данной дисциплины обучающиеся должны демонстрировать свободное владение понятиями и определениями электродинамики сплошных сред, знание физических законов и теорий для описания процессов, изучаемых в рамках электродинамики сплошных сред, умение правильно выбирать и применять физические законы, изучаемые в курсе электродинамики сплошных сред, для построения математических моделей систем и процессов.
|
|
ÝЛЕКТРОДИНАМИКÀ |
|
|
|
|
|
|
|
|
|
|
|
|
ÝЛЕКТРОДИНАМИКÀ |
|
|
|
|
|
|
|
ÌАГНИТОСТÀÒÈÊÀ |
|
ÏÐÎÂÎÄÿÙÈÕ ÑÐÅÄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ÝЛЕКТРОДИНАМИКÀ ДИЭЛЕКТРИКОВ
ÝЛЕКТРОСТÀÒÈÊÀ
ÔЕРРОГИДРО-
ДИНАМИКÀ
ÝЛЕКТРОГИДРО-
ÌАГНИТНАÿ |
|
ДИНАМИКÀ |
|
|
||
ДИНАМИКÀ |
|
|
|
|
|
|
ТВЕРДОГÎ ÒÅËÀ |
|
|
|
|
|
|
|
|
|
ÝЛЕКТРОСТÀÒÈÊÀ |
|||
|
|
|
|
|
||
|
|
|
|
|
ÏÐÎÂÎÄÿÙÈÕ ÑÐÅÄ |
|
|
ÌАГНИТНАÿ |
|||||
|
|
|
||||
|
|
|
||||
ГИДРОДИНАМИКÀ
ÝЛЕКТРОСТÀÒÈÊÀ ДИЭЛЕКТРИКОВ
ÒÅÎÐÈÿ УПРУГОСТИ
÷ ÃИДРОДИНАМИКÀ È ПЛАСТИ НОСТИ
ÌÅÕÀÍÈÊÀ СПЛОШНЫХ СРЕÄ
Учебное пособие состоит из двух частей. Первая часть включает известный из курса общей физики материал, используемый для повторения, а также новый материал. Ключевыми вопросами первой части являются вывод системы уравнений Максвелла для сплошной среды и вывод уравнения переноса магнитного поля посредством движущейся среды. Для вывода системы уравнений Максвелла, которые описываются в седьмой главе, используется изложенный ранее материал. Эти сведения собираются воедино при выводе итоговой системы уравнений.
8
Уравнение переноса магнитного поля является базовым для электродинамики сплошных сред и активно используется во второй части. При изложении материала используется система единиц СИ.
Во второй части излагается материал, который условно можно разделить на два раздела: процессы, в которых переносом магнитного поля посредством движущейся среды можно пренебречь, и процессы, в которых перенос магнитного поля движущейся средой имеет ключевое значение. К первой группе процессов относим те, которые происходят при относительно медленных движениях электропроводной среды с умеренной величиной электрической проводимости. Здесь основное внимание уделено генерации движения электропроводной среды посредством действия электрических и магнитных полей. Процессы второй группы происходят либо при экстремальных значениях электропроводности – в сверхпроводящих средах, либо в средах, скорость движения которых велика. При таких условиях движущаяся электропроводная среда способна не только переносить магнитное поле, но и генерировать и поддерживать его.
9
Список обозначений
Латинские символы
A– векторный потенциал магнитного поля [Тл·м]
B– магнитная индукция [ Тл ]
c – скорость света, c = (ε0µ0)−2 ≈ 3 · 108 м/с C – константа
C– электрическая емкость [Ф]
D– электрическая индукция (смещение) [Кл/м2]
E, e |
– напряженность электрического поля [В/м] |
|||||
Ek |
– кинетическая энергия, [Дж] |
|
|
|
|
|
Ep |
– потенциальная энергия, [Дж] |
|
|
|
|
|
ep |
– плотность потенциальной энергии, [Дж/м3] |
|||||
e¯ |
– заряд электрона, e¯ = 1, 6022 · 10−19 Кл |
|
3 |
] |
||
F, f |
– интегральная [ Н ] и объемная сила [ Н/м |
|
||||
g |
– ускорение свободного падения [м/с2] |
|
|
|
||
H, h |
– напряженность магнитного поля [А/м] |
с |
|
|||
h |
– постоянная Планка, h = 6, 62 |
· |
10−34 Дж |
|
||
|
|
· |
|
|
|
|
I– сила тока [ А ]
i– мнимая единица
k |
– постоянная Больцмана, k = 1, 3806 |
· |
10−23 Дж/К |
||
j |
|
|
2 |
] |
|
– плотность тока свободных зарядов [ A/м |
|
||||
jd |
– плотность тока связанных зарядов [ A/м2 ] |
||||
jm |
– плотность молекулярных токов [ A/м2 ] |
|
|
||
Le |
– индуктивность [ Гн ] |
|
|
|
|
dL, L |
– единичная длина контура и величина длины [ м ] |
||||
L(...) |
– функция Ланжевена |
|
|
|
|
m |
– масса [ кг ] |
|
|
|
|
m e¯ |
– масса покоя электрона, me = 9, 1096 · 10−31 кг |
||||
M |
– намагниченность [А/м] |
|
|
|
|
P |
– электрическая поляризация [В/м] |
|
|
|
|
Pem |
– вектор Умова-Пойтинга [Вт/м2] |
|
|
|
|
10
