Электродинамика сплошных сред

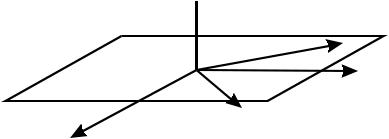
магнитном поле он будет отклоняться вбок под действием электромагнитной силы. Если ток течь не будет, а проводник будет двигаться, то он отклоняться вбок не будет, ибо электромагнитные силы, действующие на заряды, будут скомпенсированы. Однако в таком проводнике сила все-таки может возникнуть – об этом далее.

Итак, если проводник движется со скоростью V, то выражение (1.57) для тока проводимости j = σ(E + Eex) изменится. На электроны проводимости, увлекаемые средой, будет действовать сила e¯(e + µ0[V × h]), где e, h – микроскопические напряженности. Так как речь идет о макроскопической величине j, то при замене в макроскопическом выражении (1.57) макроскопического вектора E на макроскопический вектор hei + µ0[V × hhi] нужно под µ0hhi понимать среднее значение микроскопической напряженности, которое равно индукции B.

Другими словами, в движущихся средах сила, действующая на заряды среды, определяется не электрическим полем E, а эффективным полем (рис. 1.27):

Ee f = E + [V × B].

Таким образом, в движущихся средах закон Ома выглядит следующим образом:

B

E

V

81

Слагаемое [UR × B] учитывает действие эффекта Холла. В дальнейшем чаще всего мы будем пользоваться законом Ома без учета эффекта Холла и внешнего ЭДС:

1.7.3. Уравнение переноса поля

Применим оператор ротора к уравнению Ампера-Максвелла (1.149) в проводнике, при этом пренебрежем током смещения и подставим выражение для закона Ома в виде (1.161). В результате получим

После преобразований и использования уравнения (1.148) получим

уравнение переноса индукции магнитного поля

Запишем это уравнение в безразмерном виде, выбирая характерную скорость V0 и длину L0:

Здесь появляется безразмерное магнитное число Рейнольдса,

которое определяется через характерные скорость и длину а также магнитную вязкость νm .

82

1.8.Электромагнитные волны

1.8.1. Электромагнитные волны в вакууме

Запишем систему Максвелла для вакуума, когда j = 0, ε = 1, µ = 1:

Первые два уравнения можно интерпретировать как «уравнения движения» электромагнитного поля. Это поле должно быть переменным во времени и неоднородным в пространстве. Обязательно должны присутствовать оба поля – как электрическое, так и магнитное. Энергия обоих полей w должна быть одной и той же:

Оба поля должны быть взаимно ортогональны: E · H = 0. Уравнения (1.165) и (1.166) преобразуются к следующему виду:

Уравнения (1.171) и (1.170) являются волновыми, следовательно, поля E и H могут распространяться в пространстве со скоростью c и существовать в виде электромагнитной волны. Электромагнитное поле с описанными свойствами является самостоятельным физическим объектом, который можно бы было рассматривать как одну из форм вещества, так как поиски особой среды – эфира, колебания которого и должны были являться электромагнитными волнами, – не увенчались

83

успехом. Таким образом, электромагнитные волны не распространяются в среде, а летят в вакууме наподобие свободного «тела». Вследствие наличия второй производной по времени в уравнениях движение волн обладает важным свойством – обратимостью во времени. Это значит, что если формально изменить знак времени (t → −t), то уравнения не изменятся и, значит, при одинаковых начальных условиях движение будет одинаковым в обоих случаях.

Для решения этих уравнений будем использовать скалярный ϕ и векторный A потенциалы, определяемые следующим образом:

Подставим эти выражения в уравнение (1.165) и получим

Векторный потенциал является вспомогательной величиной, и при заданном H его выбор неоднозначен. Величина поля H не изменится, если произведено преобразование A0 = A(r) + Of (r), где f (r) – произвольная скалярная функция, ротор градиента которой равен нулю. Выбор конкретного вида f (r), а следовательно, и A(r) называется калибровкой потенциала. В данном случае будет использована калибровка Лоренца, определяемая выражением

Если в уравнение (1.167) подставить определение скалярного потенциала и использовать при этом калибровку (1.173), то получаем

∂

div E = −4ϕ − ∂t div A = 0,

1 ∂2ϕ

4ϕ − c2 ∂t2 = 0.

84

В итоге получаем уравнения Даламбера для векторного и скалярного потенциалов в вакууме

Простейшим типом волн являются плоские волны, в которых все величины A, E, H, ϕ зависят только от одной координаты, например z. У всяких волн ту поверхность, во всех точках которой колебания имеют одинаковую фазу, называют фронтом волны. Плоские волны имеют плоский фронт волны A(z) = C , волновая поверхность является плоскостью z = C .

Уравнения Даламбера для плоской волны имеют вид

а калибровочное условие дает для плоской волны Az = C , причем эту постоянную можно положить равной нулю, так как Az не дает вклада в поле. Плоская волна распространяется вдоль нормали к волновой поверхности (вдоль оси Z). Условие Az = 0 означает, что волна является поперечной, т.е. плоская волна описывается двумерными векторами. В силу того, что волна может распространяться в обе стороны, решение уравнений имеет следующий вид:

A(z, t) = A1(z − ct) + A2(z + ct), ϕ(z, t) = ϕ1(z − ct) + ϕ2(z + ct).

В этом легко убедиться, если подставить решения в исходные уравнения, помня при этом, что

85

1.8.2.Энергия, давление, импульс и масса электромагнитного поля

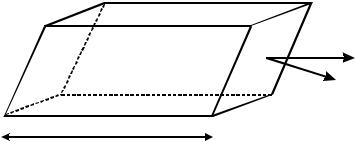
Рассмотрим в поле электромагнитной волны произвольную площадку S и вычислим энергию 4W, переносимую электромагнитной волной через эту площадку за малое время 4t. Для этого построим на площадке S , как на основании, параллелепипед (см. рис. 1.28), ребра которого параллельны скорости волны c и имеют длину c4t. Объем этого параллелепипеда 4V = S c4t cos α, где α – угол между нормалью к площадке S и скоростью c. Через площадку пройдет энергия

4W = w4V = wS c4t cos α,

где объемная плотность энергии электромагнитной волны w (1.169) складывается из энергий магнитного и электрического полей, c учетом

w = ε0E2 + µ0H2 = ε0E2 = µ0H2 = √µ0ε0EH.

2

Тогда изменение энергии

4W = EHS 4t cos α.

Следовательно, энергия, проходящая через площадку S в единицу времени, определяется выражением

представляет собой вектор потока электромагнитной энергии, или вектор Умова-Пойтинга. Таким образом, перенос энергии в электромагнитном поле можно охарактеризовать при помощи потока энергии | Pem | = wc. Мгновенное значение плотности энергии w и вектор УмоваПойтинга удовлетворяют соотношению Пойтинга – закону сохранения энергии:

86

с

S

Pem

n

c t

Рис. 1.28

Электромагнитные волны, встречая на своем пути какие-либо тела, оказывают на них давление. Это давление возникает из-за генерирования электромагнитной силы в теле за счет взаимодействия магнитного поля и тока, индуцированного электрическим полем внутри тела. Среднее значение этой силы, отнесенное к единице поверхности тела, и есть давление электромагнитной волны. Давление

определяется через угол падения волны на поверхность тела θ, коэффициент отражения k и интенсивность излучения,

мало и имеет порядок 10−5 Па.

Вследствие существования давления электромагнитное поле имеет механический импульс. За единицу времени тепло получает импульс поля, заключенный в параллелепипеде с основанием S и высотой, равной скорости распространения поля c. Если pem – плотность импульса, то импульс тела pem S c равен импульсу силы wS . Следовательно, pem = w/c. Выражая это в векторном виде через вектор УмоваПойтинга, получаем для вектора плотности импульса

87

Импульс какого-либо тела есть произведение массы этого тела на его скорость, следовательно, электромагнитному полю присуща определенная масса. Пусть ρem – плотность электромагнитного поля. Тогда плотность импульса единицы объема поля есть pem = ρem c. С другой стороны, согласно (1.183) та же плотность импульса pem = Pem /c2. Следовательно,

c ρem = Pem /c2.

Поток электромагнитной энергии выражается через объемную плотность энергии следующим образом: Pem = wc. Отсюда получаем соотношение

w = ρem c2.

Это соотношение между массой и энергией справедливо не только для единицы объема, но и для любого объема. Поэтому, если mem – масса поля, W – его энергия, то

1.8.3. Электромагнитная масса движущегося заряда

Рассмотрим движущийся электрический заряд. Вокруг него образуется электромагнитное поле, которое обладает импульсом. Поэтому полная масса увеличится. Эта дополнительная масса, связанная с электромагнитным полем, называется электромагнитной массой тела. Приращение энергии тела

dW = c2dm.

По второму закону Ньютона (с учетом зависимости массы от скорости, пользуясь определением энергии dW = FdL = FUdt) получаем

Тогда

dm = 1 d(U2/c2) . m 2 1 − U2/c2

Интегрируя это уравнение, получаем

88

где через m0 обозначена постоянная интегрирования. При U2/c2 → 0, m → m0, таким образом, m0 имеет смысл покоящейся электромагнитной массы. При быстрых движениях электромагнитная масса увеличивается с ростом скорости.

Существует гипотеза, что инерция электрона обусловлена инерцией создаваемого им поля. Однако не следует отождествлять m0 с массой электрона, так как это масса поля покоящегося электрона, которая совсем не обязательно равняется массе самого электрона. Предположим, что все-таки вся масса электрона имеет электромагнитное происхождение, и будем представлять себе электрон в виде шарика с радиусом a, а его заряд распределен равномерно по поверхности. Будем считать, что электрон покоится (H = 0), и найдем полную энергию. Учитывая, что плотность энергии w = ε0E2/2, где напряженность поля E = e¯/(4πε0r2), и выбирая элемент объема в виде dV = 4πr2dr, получаем

Приравнивая эту энергию m0c2, получаем связь между m0 и радиусом a:

Из этого соотношения нельзя определить массу покоящегося электрона, так как неизвестно, какое значение радиуса нужно брать в этой модели электрона в виде шарика. Можно поступить наоборот – найти, какой радиус должен иметь заряженный шарик, чтобы его электромагнитная масса была равна массе покоящегося электрона:

Величина a имеет название классического радиуса электрона. Эта величина не характеризует размеры электрона, но она дает характерную длину, определяющую порядок величины нижнего предела области применимости классической электродинамики, т.е. a – минимальная длина. На расстояниях меньше этой длины классическая электродинамика принципиально не может быть справедлива.

89

1.8.4. Монохроматическая волна. Поляризация волны

Решением уравнения Даламбера (1.177) является гармоническая плоская волна вида

где AR и AL – комплексные амплитуды; k – пространственное волновое число; ω – временная круговая частота волны, связанная с частотой ν, периодом T и длиной λ волны следующими соотношениями:

ω = kν = 2πν, T = 2π = λ, λ = 2π/k.

λω ν

Такая волна обладает свойством периодичности, т.е. A(z + λ, t) = A(z, t) и A(z, t + T ) = A(z, t). Связь между комплексным и действительным A Re представлениями гармонической волны дается равенством

A Re (z, t) = Re A(z, t).

Плоская волна описывается двумерным вектором, поэтому при заданных частоте и направлении распространения у волны остается еще одна, внутренняя степень свободы, которая называется поляризацией волны. В общем случае, выражение (1.188) описывает эллиптическую поляризацию волны: в каждой точке пространства вектор A вращается

счастотой ω, не изменяясь по абсолютной величине.

Вчастном случае, когда AR = 0 или AL = 0, происходит круговая поляризация волны. При этом пространственная конфигурация поля представляет собой левую или правую спираль соответственно. Не менее важным является другой частный случай, когда эллипс вырождается в отрезок, т.е. его малая полуось обращается в нуль. Это происходит, когда AR = ±AL = A0/2. Тогда волна оказывается линейно поляризованной или плоскополяризованной и описывается выражением

Произвольная эллиптически поляризованная волна может быть представлена как суперпозиция либо двух круговых поляризаций, либо двух линейных. Направление последних естественно принять за оси X и Y, тогда получаем

90