
- •Министерство образования и науки Российской федерации
- •Кафедра математики и математических методов в экономике
- •ЧИСЛЕННЫЕ МЕТОДЫ
- •Хабаровск 2014
- •1.1. Постановка задачи о приближении функций
- •1.2. Метод множителей Лагранжа
- •Идея метода – искать полином не в виде (1.2), а как
- •Схема построения полиномов Лагранжа
- •Шаг 2. Пусть x – переменная. Составим произведение
- •Шаг 3. Раскрывая внешние скобки, можно получить многочлен степени n
- •Пример. По таблице
- •Шаг 1. Находим коэффициенты
- •Шаг 3. Раскрыв скобки, получим
- •1.3. Метод разделённых разностей и полиномы Ньютона
- •Часть 1. Разностные аналоги производных
- •Часть 2. Рекурсивное вычисление функции
- •Пример. Известна таблица значений функции
- •Ответ: значения полинома Ньютона равны 18 в точке 2 и 2,2401 в точке 0,7.
- •Аналогично
- •Продифференцировав каждое слагаемое три раза, получим
- •1.5. Метод наименьших квадратов
- •Поиск линейной зависимости
- •Подставив суммы в систему (1.11), получим
- •Подставив найденные суммы в систему (1.12), получим
- •Пример 4. По приведённым данным
- •Отсюда очевидным образом имеем, что
- •Схема метода касательных
- •Вычисление корней при помощи метода простых итераций
- •Составим систему
- •Соответствующая линейная система имеет вид
- •Таблица 2.3 – Решение примера 2
- •Общая схема метода
- •Остаётся сравнить значения
- •Общая схема метода золотого сечения
- •Пусть функция f(x) задана таблицей
- •Проинтегрировав, получаем, что
- •Последовательно находим
- •Интегрируя каждое слагаемое, получим, что
- •Тогда интеграл сводится к
- •Проинтегрировав каждое слагаемое, получим
- •По теореме об интегрировании сходящихся степенных рядов
- •Если интеграл определённый, то
- •Найдём значения
- •По формуле трапеций получим
- •По формуле Симпсона будет
- •По формуле парабол
- •Поскольку значения на концах не зависят от числа точек и
- •Ответ:
- •Шаг 4. Ответ:
- •Тогда
- •Ответ:
- •Ответ:
- •Формула метода 3-го порядка точности:
- •Ответ:
- •Формула метода 4-го порядка точности
- •Все дальнейшие вычисления аналогичны и приведены в таблице.
- •Таблица (начало)
- •Таблица (окончание)
- •Ответ:
- •Пример 1. Решим систему
- •Ответ:
- •Последнее преобразуется к виду
- •Задачу (5.10) – (5.11) будем записывать в виде операторного уравнения
- •Из ограниченности третьей производной следует, что
- •Таким образом, точность близости будет О(h).
- •В силу граничных условий имеет место и неравенство
- •Если yh есть решение уравнения (5.12), то из (5.27) имеем оценку
- •Замечание о делении отрезка на части
- •Решение уравнений делением отрезка
- •Метод секущих (хорд)
- •При реализации в EXCEL достаточно заполнить строчку
- •Метод касательных
- •Реализация метода мало отличается от метода секущих, заполняем строку
- •Таблица 6.1 – Решение уравнения
- •Подбор полиномов, проходящих через точки
- •Таблица 6.2 – Поиск полинома при помощи обратной матрицы
- •Полиномы Лагранжа
- •Таблица 6.3 – Построение полинома Лагранжа
- •Таблица 6.4 – Построение полинома Ньютона
- •Метод Эйлера решения задачи Коши
- •Таблица 6.5 – Решение уравнения методом Эйлера
- •Приближённое интегрирование
- •Таблица 6.6 – Вычисление интеграла методом трапеций и методом Симпсона
- •ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
- •Часть 1. Задания для работы без пакетов прикладных программ
- •Задание 1. Решение уравнений
- •Задание 2. Метод простых итераций
- •Задание 3. Метод простых итераций в приближённых вычислениях
- •Задание 4. Полиномы Лагранжа и Ньютона
- •Задание 5. Метод наименьших квадратов
- •Задание 6. Приближённое интегрирование
- •Задание 7. Задача Коши
- •Часть 2. Задания для работы в пакете EXCEL
- •Задание 1. Приближение функций полиномами
- •Задание 2. Задача Коши
- •Задание 3. Системы дифференциальных уравнений
- •Задание 4. Задача Коши 2-го порядка
- •Задание 5. Приближённое интегрирование
- •Задание 7. Метод Ньютона решения систем нелинейных уравнений
- •Задание 9. Применение рядов в приближённом интегрировании
- •Оглавление
где n – число пар значений, а неизвестны параметры a и b. Систему 2-го порядка можно решить любым удобным способом (например, по формулам Крамера).
Из тех же соображений при подборе квадратичной зависимости y ax2 bx c получается система
a xk4 |
b xk3 c xk2 xk2 yk , |
|
||||||||
|
3 |
|
|
2 |
c xk |
xk yk , |
(1.12) |
|||
a xk |
b xk |
|||||||||
|
k |
|
|
k |
|
|
|
k |
|
|
a x2 |
b |
x |
|
cn |
|
y |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
с неизвестными a, b, c.
Пример 1. В таблице приведены 4 пары значений:
х |
–3 |
0 |
1 |
5 |
|
|
|
|
|
у |
–2 |
–1 |
2 |
6 |
|
|
|
|
|
Подобрать методом наименьших квадратов линейную функцию y ax b . Решение. Найдём необходимые суммы:
xk 3 0 1 5 3 ;
yk 2 1 2 6 5 ;
xk2 3 2 02 12 52 35 ;
xk yk 3 2 0 1 1 2 5 6 38 .
Подставив суммы в систему (1.11), получим
35a 3b 38,
3a 4b 5.
Решение этой системы – числа a 1,046 и b 0,466 . Таким образом, теоретическая линейная функция y 1,046x 0,466 .
Ответ: |
y 1,046x 0,466 . |
|
Найдём |
теоретические значения |
функции y xk 1,046xk 0,466 в узловых |
точках таблицы: |
|
|
y 3 1,046 3 0,466 2,672 ; |
y 0 1,046 0 0,466 0,466 ; |
|
y 1 1,046 1 0,466 1,512 ; |
y 5 1,046 5 0,466 5,70 . |
|
Сумма квадратов отклонений теоретических значений от фактических:
y xk yk 2 2,672 3 2 0,466 1 2 1,512 2 2 5,70 6 2 2,929 ,
17
и её невозможно уменьшить ни при каких других а, b. Функция y 1,046x 0,466 даёт лучшее приближение по сравнению со всеми линейными функциями.
Например, попытавшись провести прямую по двум точкам, давшим наибольшие отклонения, то есть по точкам (–3,–2) и (0,–1), получим y 0,333x 1 . Тогда в этих точках отклонения составят 0, в точке (1,2) получим y 1 0,333 1 1 0,667 , но в точке (5,6) будет не 5,70, а y 5 0,333 5 1 0,667 и
из-за этого общее отклонение станет намного больше:
0 0 0,667 2 2 0,667 6 2 35,533.
Тем не менее можно учесть отклонение в точках (–3,–2) и (0,–1), считая например, что все точки находятся не на прямой, а на дуге параболы, что показывает следующий пример.
Пример 2. По данным примера 1 найти функцию y ax2 bx c .
Решение. Необходимые произведения и суммы удобно найти в таблице, за-
полняя столбцы до |
x 4 |
включительно. Последние три столбца заполняются, ко- |
||||||||||||||
гда a, b, c станут известны, и необязательны для решения. |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
x |
y |
x 2 |
|
x 3 |
x 4 |
xy |
x 2 y |
y xk |
y xk yk |
|
y y |
k |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
–3 |
–2 |
9 |
|
–27 |
81 |
6 |
–18 |
–2,163 |
–0,163 |
|
0,027 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
0 |
–1 |
0 |
|
0 |
0 |
0 |
0 |
0,046 |
1,046 |
|
1,094 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3 |
1 |
2 |
1 |
|
1 |
1 |
2 |
2 |
1,019 |
–0,981 |
|
0,961 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
4 |
5 |
6 |
25 |
|
125 |
625 |
30 |
150 |
6,098 |
0,098 |
|
0,010 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
3 |
5 |
35 |
|
99 |
707 |
38 |
134 |
|
0 |
|
2,092 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставив найденные суммы в систему (1.12), получим |
|
|
|
|
||||||||||||
|
|
|
|
|
|
707a 99b 35c 134, |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
35b 3c |
38, |
|
|
|
|
|
|
|
|
|
|
|
|
|
99a |
|
|
|
|
|
|
||||
|
|
|
|
|
|
35a |
3b 4c 5. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решив эту систему, получаем |
a 0,059, b 0,914, c 0,046 , и |
теоретическая |
||||||||||||||
функция y 0,059x2 |
0,914x 0,046 . |
|
|
|
|
|
|
|
|
|
||||||
Подставив все xk в полученную функцию, найдём теоретические значения y xk и заполним последние три столбца. Общее отклонение 2,092 меньше, чем
18
2,929 при линейном приближении. Параболическая функция точнее учитывает данные задачи, чем линейная.
Ответ: y 0,059x2 0,914x 0,046 .
Если при поиске параболической функции уменьшение общего отклонения невелико и высокая точность в дальнейших действиях не нужна, предпочтительнее выбрать линейную функцию как более простую. Так, построив по четырём точкам примера 2 кубическую параболу, получим отклонение, равное 0, но это противоречит самой цели МНК – с меньшими затратами получить простую функцию. Более того, коэффициент при x 3 будет невысок.
Встроенная в пакет EXCEL функция ЛИНЕЙН позволяет сразу получить коэффициенты линейной зависимости по входным данным. Её действие как раз основано на изложенном алгоритме. Более того, с помощью функции ЛИНЕЙН можно найти зависимость общего вида
варительно вычислив значения всех базисных функций в точках xk .
Некоторые функции приходится преобразовывать к зависимости, допускающей применение МНК. Так, попытка найти коэффициенты а, p для функции
y ax p , непосредственно дифференцируя сумму |
|
axkp yk 2 по этим пара- |
|||||
метрам, приведёт к системе |
|
|
|
|
|
|
|
|
2 p |
|
p |
, |
|
|
|
a xk |
yk xk |
|
|
|
|||
|
x2 p ln x |
|
|
x p ln x , |
|||
a |
y |
||||||
|
k |
k |
|
k |
k |
k |
|
решить которую невозможно. Как действовать в таких случаях, покажем на нескольких примерах.
Пример 3. В таблице приведены пять пар значений:
х |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
у |
1,8 |
4,75 |
8,38 |
12,54 |
17,13 |
|
|
|
|
|
|
Подобрать методом наименьших квадратов функцию y ax p . Решение. Прологарифмируем равенство:
ln y ln ax p ln a ln x p ln a p ln x , и обозначим B ln a, Y ln y, X ln x .
Задача свелась к поиску зависимости Y pX B по известному алгоритму.
19
Составим таблицу:
х |
у |
Х |
Y |
X 2 |
XY |
1 |
1,8 |
0 |
0,587 8 |
00 |
0 |
|
|
|
|
|
|
2 |
4,75 |
0,693 1 |
1,558 1 |
0,480 5 |
1,080 0 |
|
|
|
|
|
|
3 |
8,38 |
1,098 6 |
2,125 8 |
1,206 9 |
2,335 5 |
|
|
|
|
|
|
4 |
12,54 |
1,386 3 |
2,528 9 |
1,921 8 |
3,505 8 |
|
|
|
|
|
|
5 |
17,13 |
1,609 4 |
2,840 8 |
2,590 2 |
4,572 1 |
|
|
|
|
|
|
|
|
4,787 5 |
9,641 5 |
6,199 5 |
11,493 5 |
|
|
|
|
|
|
В таблице X ln x , Y ln y , а в последней строке указаны суммы каждого столбца. Подставив суммы так же, как в примере 1, и учитывая, что у нас пять пар данных, получим систему
6,199 5 p 4,787 5B 11,463 54,787 5 p 5B 9,641 5,
из которой p 1,400 0, B 0,587 8 .
Поскольку B ln a и соответственно a eB , находим a e0,5878 1,800 0 . Таким образом, если предполагается степенная зависимость, то наиболее точно она задаётся формулой y 1,8x1,4 . Проверка даёт почти нулевое отклонение.
Ответ: y 1,8x1,4 .
Пример 4. По приведённым данным
|
х |
–0,5 |
–0,2 |
|
0 |
|
0,5 |
|
0,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у |
1,5 |
1,4 |
|
1,3 |
|
1,5 |
|
1,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
A |
|||
подобрать при помощи МНК функцию |
|
. |
|||||||||
ln cos x b |
|||||||||||
Решение. Чтобы привести функцию к виду, допускающему подбор методом наименьших квадратов, обратим исходное равенство:
1 |
|
ln cos x b |
|
1 |
ln cos x |
b |
. |
|
|
|
|
||||
y |
|
A |
|
A |
A |
||
Обозначив K 1/ A, B b / A, получаем зависимость Y KX B , где Y 1 / y
и X ln cos x .
20

Подберём коэффициенты K, B так же, как в примере 1, и затем найдём интересующие нас A 1/ K и b BA B / K . Вычисляем:
|
|
|
|
|
|
|
|
|
|
|
х |
у |
Х |
Y |
X 2 |
XY |
y xk |
y xk yk |
y y |
k |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
–0,5 |
1,5 |
–0,130 6 |
0,666 7 |
0,0171 |
–0,087 1 |
1,485 |
–0,015 |
0,000 22 |
||
|
|
|
|
|
|
|
|
|
||
–0,2 |
1,4 |
–0,020 1 |
0,714 3 |
0,0004 |
–0,014 4 |
1,365 |
–0,035 |
0,001 22 |
||
|
|
|
|
|
|
|
|
|
||
0 |
1,3 |
0 |
0,769 2 |
0 |
0 |
1,345 |
0,045 |
0,002 04 |
||
|
|
|
|
|
|
|
|
|
||
0,5 |
1,5 |
–0,130 6 |
0,666 7 |
0,0171 |
–0,087 1 |
1,485 |
–0,015 |
0,000 22 |
||
|
|
|
|
|
|
|
|
|
||
0,8 |
1,8 |
–0,361 4 |
0,555 6 |
0,1306 |
–0,200 8 |
1,819 |
0,019 |
0,000 37 |
||
|
|
|
|
|
|
|
|
|
||
|
|
–0,642 7 |
3,372 5 |
0,1652 |
–0,389 4 |
|
0 |
0,004 07 |
||
|
|
|
|
|
|
|
|
|
|
|
В последней строке, как обычно, указаны суммы чисел в столбцах. Составляем систему
|
|
0,165 2K 0,6472B 0,389 4 |
||
|
|
|
3,372 5, |
|
|
|
0,642 7K 5B |
||
из которой K 0,536, |
B 0,743 Тогда по приведённым выше формулам |
|||
|
A 1/ 0,536 1,866; |
b 0,743 1,866 1,387 . |
||
Таким образом, |
y |
1,866 |
. В последних столбцах таблицы приведены |
|
|
||||
ln cos x 1,387 |
||||
теоретические значения функции, отклонения от фактических и их квадраты.
|
1,866 |
|
|
Ответ: |
y |
|
. |
ln cos x 1,387 |
|||
Замечание 1. Значения функции, приведённые в условии, получены округле-
|
2 |
|
нием значений функции |
y ln cos x 1,5 |
, найденных в указанных точках x, до 1 |
знака после запятой. При округлении входных данных до целых чисел МНК дает
функцию |
y |
0,709 |
, а при округлении до двух знаков получается, что |
||
|
|
||||
ln cos x 0,766 |
|||||
y |
1,972 |
|
. |
|
|
|
|
|
|
||
|
|
|
|
||
ln cos x 1,481
Замечание 2. Таким же образом можно найти более сложную зависимость
y |
|
A |
|
, взяв Y 1/ y 2 и выполнив действия по той же схеме. |
|
|
|
|
|||
ln cos x b |
|||||
|
|
|
|
21
1.6 Интерполяция сплайнами
Здесь, как и ранее, рассматривается приближение функции f (x) , заданной аналитически на отрезке [a;b] или таблицей (1.1) другой функцией (x) . При этом искомая на отрезке [a;b] функция (x) в заданных точках xi должна при-
нимать значения равные f (xi ) .
В первых пунктах роль (x) выполняли интерполяционные многочлены Лагранжа и Ньютона, которые различаются только формой записи. Однако, приближение функции с помощью многочленов оказывается малопригодным, если приближаемая функция f (x) имеет небольшое количество производных, а такие функции чаще всего встречаются в приложениях. Это обстоятельство и привело к необходимости введения сплайнов.
Для определённости будем рассматривать приближение функции f (x) на отрезке [a;b] . Разобьём его на части [x0 ; x1 ] , … , [xn 1 ; xn ] , при этом x0 a , xn b и x0 x1 xn . Обозначим это разбиение отрезка через , а разность xi xi 1 через hi .
Сплайном Sm ( f , x) порядка m называется функция, являющаяся многочле-
ном порядка m на каждом из отрезков i |
[xi 1 ; xi ] , т. е. на каждом отрезке i |
|||||
S |
m |
( f , x) P |
(x) a |
a |
x1 a xm |
(1.13) |
|
im |
i0 |
i1 |
im |
|
|
иудовлетворяет условиям:
1)Sm ( f , x) непрерывна вместе со своими производными до порядка m 1 в
узлах интерполирования |
x1 , , xn . То есть |
Pim (xi ) P(i 1)m (xi ) |
для i 1, , n 1 и |
||||||
для |
всех j 1, , m 1 |
выполняется |
равенство |
P( j ) |
(x |
) P( j ) |
(x |
) |
для |
|
|
|
|
im |
i |
(i 1)m |
i |
|
|
i 1, , n 1; |
|
|
|
|
|
|
|
|
|
2) |
Sm ( f , xi ) f (xi ) для i 0,1, , n . |
|
|
|
|
|
|
|
|
Из определения следует, что для построения сплайна порядка m надо задать значения m 1 коэффициента, так как на каждом отрезке [xi 1 ; xi ] сплайн являет-
ся многочленом степени m . Условия 1), 2) задают n(m 1) (m 1) ограничений.
22
При m 1 число ограничений равно числу неизвестных и коэффициенты сплайна находятся из условия 2). Если m 2 , то число ограничений меньше числа неизвестных коэффициентов и, следовательно, для однозначного определения коэффициентов надо задать дополнительные условия.
Обычно сплайны степени m 2 p 1 находят из решения следующей задачи:
Задача 1. Среди сплайнов Sm ( f , x) |
найти такой, |
на котором интеграл от |
|
b |
2 |
|
|
Sm ( f , x) ( p) |
|
|
|
квадрата p -й производной сплайна |
dx |
достигает наименьшего |
|
a |
|
|
|
значения. |
|
|
|
Аналогично сплайны чётной степени m 2 p находят из решения задачи 1. Сплайны, являющиеся решениями задачи 1, называются интерполяционными
сплайнами. Имеют место теоремы.
Теорема 1. Если n p 1 , то задача 1 имеет единственное решение.
Теорема 2. Если h max hi |
| i 1, n и Sm решение задачи 1, то найдётся по- |
||||||||||
стоянная C такая, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
m |
f (x) |
|
|
|
C |
Ch p 0,5 |
||
|
|
|
|
||||||||
и для производных порядка j |
( j p 1) |
|
|||||||||
|
|
||||||||||
|
Sm( j ) |
f ( j) |
|
C |
Ch p 0,5 j . |
||||||
|
|
||||||||||
|
|
|
|
|
|
|
|
||||
Так как сплайны на каждом отрезке [xi 1 ; xi ] являются многочленами, то ин-
теграл в задаче 1 является квадратичной формой от коэффициентов сплайна. Поэтому решение задачи 1 сводится к решению системы линейных алгебраических уравнений для коэффициентов сплайна. В частности, для сплайнов третьего по-
рядка задача 1 сводится к решению системы из n 1 |
уравнения с n 1 неизвест- |
|||||||
ной M (M |
, , M |
n 1 |
) |
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
CM D . |
|
|
(1.14) |
|
Элементы матрицы-столбца D задаются равенствами |
|
|||||||
|
|
di |
|
f (xi 1 ) f (xi ) |
|
f (xi ) f (xi 1 ) |
. |
(1.15) |
|
|
|
hi |
|||||
|
|
|
|
hi 1 |
|
|
||
Матрица |
C является трёхдиагональной, и |
её элементы |
задаются |
|||||
соотношениями |
|
|
|
|
|
|
|
|
23
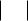
|
hi |
|
|
ïðè |
|
||
|
|
6 |
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
hi 1 |
|||
|
hi |
|
|||||
Cij |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
3 |
|
||
|
h |
1 |
|
|
|
||
|
|
i |
|
ïðè |
|||
|
6 |
|
|||||
|
|
|
|
|
|||
|
0 |
|
|
ïðè |
|
||
|
|
|
|
|
|
|
|
j i 1,
ïðè j i ,
(1.16)
j i 1,
i j 1.
Решив систему (1.14) и введя M 0 M n 0 для каждого i от 1 до n на отрез-
ке i определим многочлен третьей степени:
|
(x |
i |
x)3 |
(x x |
i |
1 |
)3 |
|
|
Pi3 (x) M i 1 |
|
|
M i |
|
|
|
|||
|
|
|
6hi |
|
|
||||
|
|
|
6hi |
|
|
|
|||
|
M |
h2 |
x |
i |
x |
|
M h2 |
|
|
|
i 1 i |
|
|
|
i i |
||
f (xi 1 ) |
|
|
|
|
|
|
f (xi ) |
|
|
6 |
|
|
hi |
6 |
|||
|
|
|
|
|
||||
x xi 1 |
|
|
|
|
|
. |
(1.17) |
|
|||
|
hi |
||
|
|
|
|
В качестве реализации данного алгоритма рассмотрим следующий пример.
Пример. Построить сплайн третьего порядка на отрезке [0;4] для разбиения
с равномерным шагом h 1 для функции, заданной таблицей |
|
|
||||||||
|
xi |
|
0 |
|
1 |
|
2 |
|
4 |
|
|
|
|
|
3 |
|
|||||
|
f (xi ) |
|
0 |
|
0,71 |
|
1 |
0,71 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Решение. По формулам (1.15) построим матрицу D . Так как hi h xi xi 1 ,
то
di f (xi 1 ) 2 f (xi ) f (xi 1 ) .
Следовательно, d1 0,42 , |
d2 0,58 , |
d3 |
0,42 . Матрица системы C будет |
|||||||
иметь вид в силу (1.16) |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
0 |
|
||
|
|
|
|
|
|
|||||
|
|
3 |
6 |
|
|
|
|
|||
|
C |
|
1 |
|
2 |
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
3 |
6 |
||||||
|
|
|
||||||||
|
|
|
|
|
||||||
|
|
|
0 |
|
|
1 |
|
2 |
|
|
|
|
|
|
6 |
|
|
|
|
||
|
|
|
|
|
|
|
3 |
|||
24
Решив систему (1.14), получим M1 0,471, M2 0,634 , M 3 0,471. Счи-
тая M0 M 4 0 , получим значения многочленов третьей степени на каждом из
отрезков [xi 1; xi ] . Из формулы (1.17) следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
а) на отрезке [0;1] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
(1 x)3 |
|
|
(x 0)3 |
|
|
|
1 x |
|
|
|
|
|
|
|
0,471 x 0 |
|
|
|
|
|
|
|
|
3 |
|
|||||||||||||||||||||
P13(x) 0 |
|
|
0,471 |
|
|
|
|
0 |
|
|
|
|
|
|
0,71 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,789x 0,079x |
|
; |
||||||||||||||||
6 |
|
6 |
|
|
|
|
|
1 |
|
|
|
|
6 |
|
|
|
1 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
б) на отрезке [1;2] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
(2 x)3 |
|
|
|
|
(x 1)3 |
|
|
|
|
0,471 |
|
2 x |
|
|
0,634 |
|
|
x 1 |
|
|
|
||||||||||||||||||||||||
P23(x) 0,471 |
|
|
|
0,634 |
|
|
|
|
|
|
|
|
0,71 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||
6 |
|
|
6 |
|
|
|
|
|
6 |
|
|
|
1 |
|
|
6 |
1 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
0,079 (2 x)3 0,106 (x 1)3 |
|
0,789 (2 x) 1,106 (x 1) ; |
||||||||||||||||||||||||||||||||||||||||
в) на отрезке [2;3] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
(3 x)3 |
|
|
|
(x 2)3 |
|
|
|
|
0,634 |
3 x |
|
|
|
|
|
0,471 |
|
|
x 2 |
|
|
|
|||||||||||||||||||||||
P33(x) 0,634 |
|
|
|
0,471 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,71 |
|
|
|
|
|
|
|
|
||||||||||||
6 |
|
|
6 |
|
|
|
6 |
|
1 |
|
|
|
6 |
1 |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
0,106 (3 x)3 |
0,079 (x 2)3 |
1,106 (3 x) 0,789 (x 2) ; |
||||||||||||||||||||||||||||||||||||||||||
г) на отрезке [3;4] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
(4 x)3 |
|
|
|
|
|
|
|
0,471 |
|
4 x |
|
|
|
|
|
|
x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
P43(x) 0,471 |
|
|
|
0 0,71 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
6 |
|
|
|
6 |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0,079 (4 x)3 0,789 (4 x) .
§2. Численные методы решения функциональных уравнений
2.1.Метод деления отрезка
Внастоящем параграфе решается задача о нахождении действительных (вещественных) корней функционального уравнения
f x 0 |
(2.1) |
c функцией f(x) действительной переменной, определённой на некотором промежутке.
Пусть функция f(x) непрерывна на некотором отрезке [a, b] и на его концах принимает значения разных знаков (f(a)f(b)<0). Тогда внутри этого отрезка, т.е. на интервале (a, b), существует по крайней мере один вещественный корень
25

уравнения (2.1). Сформулированное утверждение называется теоремой Больцано – Коши об обращении непрерывной на отрезке функции в нуль.
Будем считать, что интересующий нас корень c является единственным на интервале (a, b). Так будет в случае строго монотонных (возрастающих, убывающих) функций на (a, b). Последнее обеспечивается положительностью или отрицательностью производной на этом интервале.
В случае нескольких корней уравнения (2.1) выделяют промежутки монотонности функции f(x).
Итак, пусть на отрезке [a, b] функция f(x) удовлетворяет условиям сформулированной теоремы Больцано – Коши и имеет на нём единственный корень с. Тогда число x0 a можно считать приближённым значением этого корня с не-
достатком, а число x0 b – его приближённым значением с избытком.
Погрешность начального приближения х0 к с, очевидно, будет удовлетворять неравенству c x0 b a .
Перейдём к описанию нахождения корня уравнения (2.1) методом деления отрезка (методом «вилки» или дихотомии или бисекции).
Разделим отрезок [a, b] пополам и за первое приближение х1 к с возьмём
середину отрезка [a, b], т. е. x1 a b . При этом может представиться два
2
случая:
1)f x1 0 (в этом случае c x1 и искомый корень найден);
2)f x1 0 .
Во 2-м случае на одной из половин [a, x1], [x1, b] знак f x1 совпадает или со знаком f a , или со знаком f b .
На одной из этих половин функция f x будет принимать значения разных знаков. Эту половину называют «вилкой». Обозначим её [a1, b1]. Искомый корень с находится на отрезке [a1, b1]. Абсолютная погрешность первого при-
|
|
|
b a |
. |
|
ближения удовлетворяет неравенству |
c x |
|
|||
|
|||||
|
|
||||
|
1 |
|
2 |
|
|
|
|
|
|
||
С отрезком [a1, b1] поступим так же, как и с исходным отрезком [a, b] , т. е. разделим его пополам. За второе приближение x2 возьмём середину отрезка
[a |
, b |
], т. е. число |
x |
a1 b1 |
. Если |
f x |
|
0 , то процесс завершается; если |
|
2 |
|||||||
1 |
1 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
26
|
f x2 0 , |
то процесс продолжим. При этом выполняется неравенство |
||||
|
c x |
|
|
b a |
. |
|
|
|
|
||||
|
|
|||||
|
|
|
|
|||
|
2 |
|
22 |
|
|
|
|
|
|
|
|||
Врезультате продолжения действий будут иметь место две возможности:
1)процесс завершится в результате того, что на некотором этапе значение f(x) будет равным нулю в середине некоторой из последующих половин отрезков (искомый корень с будет найден).
2)описанный процесс будет неограниченно продолжаться.
Во второй ситуации будем иметь стягивающуюся систему отрезков [a1, b1], [a2, b2], …, [an, bn],…, причём при любом n функция f(x) имеет на концах соответствующего отрезка значения разных знаков. Известно, что стягивающаяся система отрезков имеет одну общую точку, к которой сходятся обе последовательности an и bn. Можно доказать, что эта общая точка и есть с.
Таким образом, при применении данного метода за приближённое значение к искомому корню с берут число
|
|
|
x |
|
an bn |
, |
|
|
(2.2) |
|
|
|
|
|
|
||||||
|
|
|
n 1 |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
т. е. середину отрезка [a , b ], длина которого равна |
b a |
. За первое приближе- |
||||||||
|
||||||||||
n |
|
n |
|
|
|
2n |
|
|||
|
|
|
|
|
|
|
|
|
||
ние х1 к с берётся число |
x1 |
|
a b |
|
, которое получается из (2.2) при |
n 0 , если |
||||
|
||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
считать a0 a, b0 |
b . Абсолютная погрешность приближения xn к с удовлетворя- |
||||||
ет неравенству |
|
|
|
|
|
|
|
|
|
c x |
|
|
b a |
. |
(2.3) |
|
|
|
|||||
|
|
||||||
|
|
|
|
||||
|
|
n 1 |
|
|
2n 1 |
|
|
|
|
|
|
||||
Этим очень простым по сущности методом корень уравнения (2.1) можно вычислить с какой угодно точностью. Согласно (2.3) точность приближения хn+1 к корню с имеет порядок О(2–n–1). Это означает, что метод деления отрезка требует большой вычислительной работы.
Алгоритм метода достаточно прост.
1-й шаг. Выберем отрезок a,b так, чтобы выполнялись два условия:
а) функция f x непрерывна на a,b ;
б) на концах отрезка f x принимает значения разных знаков, то есть f a f b 0 .
27

2-й шаг. Найдём c – середину a,b как c 0,5 a b и значение f c . Если f c 0 , то корень найден. Если f c 0 , то знак f c совпадает или со знаком f a , или со знаком f b .
В первом случае решение уравнения находится на отрезке c,b . Обозначив точку c как a , получим отрезок a,b вдвое меньшей длины, где продолжаем искать корень, а предыдущая точка a нас уже не интересует.
Во втором случае (знак f c совпал со знаком f b ) решение находится наa, c . Обозначив c как b , также получаем новый отрезок a,b .
В любом случае одна из границ отрезка сохраняется, а другая сдвигается в середину отрезка. Кратко сказанное можно записать так:
– пусть |
f a 0 , тогда: если |
f c 0 , то |
a c , иначе b c ; |
– пусть |
f a 0 , тогда: если |
f c 0 , то |
b c ; иначе a c . |
При переходе к новому отрезку знаки f a и f b никогда не изменятся. Проверка. Деление отрезка и сдвиг точек проводим, пока не выполняется
какое-либо из двух условий:
а) |
|
b a |
|
2 , где − необходимая точность решения; |
|
|
|||
б) |
|
f c 0 или f c . |
||
Точность может быть задана заранее или выбрана произвольно. Если ни одно из условий не выполнено, повторяем шаг 2. Если выполнено хотя бы одно,
указываем в ответе значение с=0,5 (a+b). |
|
|
|
|
|
|
|
|
|
Пример. Решим с точностью 0,01 |
уравнение x3 |
|
|
|
|
|
|
||
x 2 . |
|
|
|
|
|||||
1-й шаг. Сводим уравнение к виду x3 |
|
|
f x x3 |
|
|
|
|||
x 2 0 . Функция |
|
x 2 |
|||||||
непрерывна при всех x 0 . |
|
|
|
|
|
|
|
|
|
Найдём любые точки, в которых у функции разный знак. Замечаем, |
|
что |
|||||||
f 0 0 : |
|
|
|
|
|
|
|
|
|
f 0 03 
 0 2 2 0 .
0 2 2 0 .
Подберём точку, где функция положительна. Подходит x 2 :
|
f 2 23 |
|
|
|
2 2 4,5858 0 . |
||
Итак, a 0, b 2 , |
f a 0, f b 0 . |
|
|
2-й шаг. Находим c 0,5 a b 0,5 0 2 1. В этой точке
28

f c f 1 13 
 1 2 2 0 .
1 2 2 0 .
Поскольку f 0 0 , f 1 0 , f |
2 0 , выбираем a 1, b 2 . |
||||
Проверка. Поскольку |
|
2 1 |
|
|
0,01 , то действия продолжаем. |
|
|
||||
|
|
|
|
|
|
2-й шаг. Находим c 0,5 1 2 1,5. В ней
f 1,5 1,53 
 3 2 0,150 3 0 .
3 2 0,150 3 0 .
Видим, что f 1 0 , f 1,5 0 , f 2 0 , поэтому a 1, b 1,5 .
Проверка. 1,5 1 0,01 . Продолжаем деление отрезка.
2-й шаг. Находим c 0,5 1 1,5 1,25; затем
f 1,25 1,253 
 1,25 2 1,164 9 0 .
1,25 2 1,164 9 0 .
Теперь f 1 0 , f 1,25 0 , f 1,5 0 , откуда a 1,25,b 1,5 .
Проверка. 1,5 1,25 0,01. Продолжаем действия.
Дальнейшие вычисления оформим в виде таблицы. Середины считаем с до-
полнительным знаком после запятой − с точностью 0,001. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
a |
f a |
c |
f c |
b |
f b |
Новый a; b |
Новая c |
|
|
|
|
|
|
|
|
|
|
1 |
–2 |
1,25 |
–1,2 |
1,5 |
0,2 |
1,25;1,5 |
1,375 |
|
|
|
|
|
|
|
|
|
|
1,25 |
–1,2 |
1,375 |
–0,6 |
1,5 |
0,2 |
1,375;1,5 |
1,438 |
|
|
|
|
|
|
|
|
|
|
1,375 |
–0,6 |
1,438 |
–0,3 |
1,5 |
0,2 |
1,438;1,5 |
1,469 |
|
|
|
|
|
|
|
|
|
|
1,438 |
–0,3 |
1,469 |
–0,04 |
1,5 |
0,2 |
1,469;1,5 |
1,484 |
|
|
|
|
|
|
|
|
|
|
1,469 |
–0,04 |
1,484 |
0,05 |
1,5 |
0,2 |
1,469;1,484 |
- |
|
|
|
|
|
|
|
|
|
Длина отрезка 1,469;1,484 меньше удвоенной точности:
|
1,484 1,469 |
|
0,015 2 0,01 0,02 , |
|
|
||
|
|
|
|
середина этого отрезка – решение уравнения с точностью 0,01. Находим c 0,5 1,484 1,469 1,476 .
Округляя до двух знаков после запятой, получаем решение x 1,48 .
Заметим, что f 1,476 0,000 7 0,01, а f 1,48 0,025 , что заметно хуже, одна-
ко в ответе приходится указывать округлённое число. |
|
|
Ответ: с точностью 0,01 решением уравнения x3 |
x 2 |
будет число x 1,48 . |
При решении сами значения функции не играют роли, если только не окажется случайно, что f c 0,01, где 0,01 – необходимая точность. Важны только знаки функции. Это удобно, поскольку знак функции в точках, достаточно уда-
29

лённых от корня, обычно очевиден, что позволяет быстро пройти первые шаги решения.
Знак функции на каждом конце отрезка не меняется в процессе сужения отрезка. А именно, если для 1-го приближения f a 0 и f b 0 , то это же будет справедливо для любого следующего приближения.
Кроме того, число шагов можно предсказать заранее.
Длина начального отрезка в примере составляла 2, и, чтобы, уменьшая её на каждом шаге в 2 раза, получить отрезок длиной менее 0,02, надо проделать не
менее |
log |
|
2 |
|
log 2 100 6,64 , то есть 7 операций деления. Общая формула чис- |
|||||
2 |
|
|
||||||||
0,02 |
||||||||||
|
|
|
|
|
|
|
|
|||
ла шагов: n |
log 2 |
b a |
, где x – целая часть числа |
x . |
||||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
2.2. Метод хорд
Метод хорд (метод секущих) сходится (приводит к решению) быстрее, чем метод деления отрезка, однако требует на каждом шаге большего числа действий. Приведём схему метода.
Пусть необходимо решить уравнение (2.1) с точностью . Выбираем произвольные точки x0 , x1 . Каждое следующее приближение, начиная с x2 , находим по формуле
xn 1 xn f xn |
xn xn 1 |
|
|
. |
(2.4) |
|||||
f xn f xn 1 |
|
|||||||||
|
|
|
|
|
||||||
Формула (2.4) есть расчётная формула метода хорд. |
||||||||||
Вычисления прекращаем, когда |
|
xn 1 xn |
|
или |
|
|
f xn 1 . |
|||
|
|
|
|
|||||||
В ответе указываем xn 1 . |
|
|
|
|
|
|
|
|||
При решении методом хорд выполнение условия |
f x0 f x1 0 гарантирует |
|||||||||
существование корня и получение его этим методом. Однако хорда (секущая) пересечёт ось абсцисс, даже если обе точки графика находятся с одной стороны от оси, поэтому условие не является необходимым. Но в любом случае надо, чтобы f x0 f x1 , иначе секущая параллельна оси OX, а при вычислении точки происходит деление на нуль.
Пример. Решить уравнение x2 |
|
|
|
|
x 3 0 с точностью 0,001. |
||||
Решение. 1-й шаг. В примере |
f x x2 |
|
3 . Вычисления проводим с |
|
x |
||||
дополнительным десятичным знаком, то есть с 4 знаками.
30

|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
x 1. |
|
|
|
|
|
|
|
|
f 0 02 |
|
|
|
|
|
|
|||||||||||||
Попробуем |
взять |
|
x |
0 |
|
и |
|
При |
этом |
|
0 3 3 |
и |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
f 1 12 |
|
3 3. Выбор неудачен, поскольку при поиске x2 |
произойдёт де- |
||||||||||||||||||||||||||||||||||||||||||||
1 |
|||||||||||||||||||||||||||||||||||||||||||||||
ление на 0. Секущая горизонтальна и не пересекает ось OX. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
2 , тогда |
|
|
f 2 22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Возьмём x |
|
|
|
|
|
2 3 0,414 2 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Итак, |
|
x0 0, f 0 3, x1 |
|
2, f 2 0,414 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
2-й шаг. Находим x2 |
|
2 0,414 2 |
|
|
2 0 |
|
|
|
2 0,414 2 |
|
2 |
|
|
|
2,320 4 ; |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
0,414 2 3 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,585 8 |
|
|
||||||||||||||
при этом f 2,320 4 2,320 42 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
2,320 4 3 0,8611. Далее, |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
x3 |
2,320 4 0,8611 |
|
|
|
2,320 4 2 |
|
|
2,104 0 , f 2,104 0 0,023 7 ; |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0,8611 0,414 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
x |
|
2,104 0 0,023 7 |
|
2,104 0 2,320 4 |
2,109 8 , |
f 2,109 8 0,0013; |
|
|||||||||||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0,023 7 |
0,8611 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x5 |
2,109 8 0,001 3 |
|
|
|
2,109 8 2,104 0 |
|
|
2,1011. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
0,001 3 0,023 7 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
3-й шаг. Поскольку |
|
x5 x4 |
|
|
|
|
|
2,1101 2,109 8 |
|
0,000 3 0,001, точность |
до- |
||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
стигнута. Более того, |
f 2,1101 0,000 096 0,0001 . Дальнейшие действия с 4 |
||||||||||||||||||||||||||||||||||||||||||||||
знаками не изменят результат: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
x6 2,1101 0,000 096 |
|
|
|
2,1101 2,109 8 |
|
|
2,1101. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
0,000 096 0,0013 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Ответ: решение уравнения с точностью 0,001 – число x 2,110 . |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
При программировании метода надо учесть, |
что знаменатель f xn f xn 1 |
||||||||||||||||||||||||||||||||||||||||||||||
может быть близок к 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Вычисления можно оформить в виде таблицы: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
n |
|
xn 1 |
xn |
|
|
|
|
f xn 1 |
|
|
|
|
|
|
|
|
f xn |
|
|
xn xn 1 |
|
|
f xn f xn 1 |
|
|
|
xn 1 |
|
||||||||||||||||||
|
1 |
|
0 |
|
|
2 |
|
|
|
|
|
|
|
–3 |
|
|
|
|
|
–0,414 2 |
|
|
2 |
|
|
|
|
2,585 8 |
|
|
2,320 4 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
2 |
|
2 |
|
|
2,320 4 |
|
–0,414 2 |
|
|
|
|
0,861 1 |
|
|
0,320 4 |
|
|
1,275 3 |
|
|
2,104 0 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
3 |
|
2,320 4 |
2,104 0 |
|
|
|
|
0,861 1 |
|
|
|
|
–0,023 7 |
|
|
–0,216 4 |
|
|
–0,884 8 |
|
|
2,109 8 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
4 |
|
2,104 0 |
2,109 8 |
|
–0,023 7 |
|
|
|
–0,001 3 |
|
|
0,005 8 |
|
|
0,022 4 |
|
|
2,110 1 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
5 |
|
2,109 8 |
2,110 1 |
|
–0,001 3 |
|
|
|
–0,000 096 |
|
|
0,000 3 |
|
|
–0,001 204 |
|
2,110 1 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В каждой строке, начиная со 2-й, три значения берутся из предыдущей. Поясним сущность описанного метода хорд, т.е. применяемую формулу (2.4).
Предположим, что функция f(x) уравнения (2.1) на исходном отрезке [a,b] имеет непрерывные производные и постоянного знака ( <0 или
