
- •Министерство образования и науки Российской федерации
- •Кафедра математики и математических методов в экономике
- •ЧИСЛЕННЫЕ МЕТОДЫ
- •Хабаровск 2014
- •1.1. Постановка задачи о приближении функций
- •1.2. Метод множителей Лагранжа
- •Идея метода – искать полином не в виде (1.2), а как
- •Схема построения полиномов Лагранжа
- •Шаг 2. Пусть x – переменная. Составим произведение
- •Шаг 3. Раскрывая внешние скобки, можно получить многочлен степени n
- •Пример. По таблице
- •Шаг 1. Находим коэффициенты
- •Шаг 3. Раскрыв скобки, получим
- •1.3. Метод разделённых разностей и полиномы Ньютона
- •Часть 1. Разностные аналоги производных
- •Часть 2. Рекурсивное вычисление функции
- •Пример. Известна таблица значений функции
- •Ответ: значения полинома Ньютона равны 18 в точке 2 и 2,2401 в точке 0,7.
- •Аналогично
- •Продифференцировав каждое слагаемое три раза, получим
- •1.5. Метод наименьших квадратов
- •Поиск линейной зависимости
- •Подставив суммы в систему (1.11), получим
- •Подставив найденные суммы в систему (1.12), получим
- •Пример 4. По приведённым данным
- •Отсюда очевидным образом имеем, что
- •Схема метода касательных
- •Вычисление корней при помощи метода простых итераций
- •Составим систему
- •Соответствующая линейная система имеет вид
- •Таблица 2.3 – Решение примера 2
- •Общая схема метода
- •Остаётся сравнить значения
- •Общая схема метода золотого сечения
- •Пусть функция f(x) задана таблицей
- •Проинтегрировав, получаем, что
- •Последовательно находим
- •Интегрируя каждое слагаемое, получим, что
- •Тогда интеграл сводится к
- •Проинтегрировав каждое слагаемое, получим
- •По теореме об интегрировании сходящихся степенных рядов
- •Если интеграл определённый, то
- •Найдём значения
- •По формуле трапеций получим
- •По формуле Симпсона будет
- •По формуле парабол
- •Поскольку значения на концах не зависят от числа точек и
- •Ответ:
- •Шаг 4. Ответ:
- •Тогда
- •Ответ:
- •Ответ:
- •Формула метода 3-го порядка точности:
- •Ответ:
- •Формула метода 4-го порядка точности
- •Все дальнейшие вычисления аналогичны и приведены в таблице.
- •Таблица (начало)
- •Таблица (окончание)
- •Ответ:
- •Пример 1. Решим систему
- •Ответ:
- •Последнее преобразуется к виду
- •Задачу (5.10) – (5.11) будем записывать в виде операторного уравнения
- •Из ограниченности третьей производной следует, что
- •Таким образом, точность близости будет О(h).
- •В силу граничных условий имеет место и неравенство
- •Если yh есть решение уравнения (5.12), то из (5.27) имеем оценку
- •Замечание о делении отрезка на части
- •Решение уравнений делением отрезка
- •Метод секущих (хорд)
- •При реализации в EXCEL достаточно заполнить строчку
- •Метод касательных
- •Реализация метода мало отличается от метода секущих, заполняем строку
- •Таблица 6.1 – Решение уравнения
- •Подбор полиномов, проходящих через точки
- •Таблица 6.2 – Поиск полинома при помощи обратной матрицы
- •Полиномы Лагранжа
- •Таблица 6.3 – Построение полинома Лагранжа
- •Таблица 6.4 – Построение полинома Ньютона
- •Метод Эйлера решения задачи Коши
- •Таблица 6.5 – Решение уравнения методом Эйлера
- •Приближённое интегрирование
- •Таблица 6.6 – Вычисление интеграла методом трапеций и методом Симпсона
- •ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
- •Часть 1. Задания для работы без пакетов прикладных программ
- •Задание 1. Решение уравнений
- •Задание 2. Метод простых итераций
- •Задание 3. Метод простых итераций в приближённых вычислениях
- •Задание 4. Полиномы Лагранжа и Ньютона
- •Задание 5. Метод наименьших квадратов
- •Задание 6. Приближённое интегрирование
- •Задание 7. Задача Коши
- •Часть 2. Задания для работы в пакете EXCEL
- •Задание 1. Приближение функций полиномами
- •Задание 2. Задача Коши
- •Задание 3. Системы дифференциальных уравнений
- •Задание 4. Задача Коши 2-го порядка
- •Задание 5. Приближённое интегрирование
- •Задание 7. Метод Ньютона решения систем нелинейных уравнений
- •Задание 9. Применение рядов в приближённом интегрировании
- •Оглавление

Установим теперь, как аппроксимирует вторую производную y (x) разностное отношение
y(x h) 2 y(x) y(x h) . h2
Если y(x) есть трижды непрерывно дифференцируемая функция, то из только что выписанных разложений по формуле Тейлора для y(x + h) и y(x – h) получим, что
y(x h) 2 y(x) y(x h) |
– |
y (x) = |
1 |
h[ y ( ξ |
) – |
y (ξ )]. |
|
|
|||||
h2 |
|
6 |
2 |
|
3 |
|
|
|
|
|
|||
Из ограниченности третьей производной следует, что
│ |
y(x h) 2 y(x) y(x h) |
– |
|
(5.24) |
|
||||
h2 |
y (x) │ с7h. |
|||
|
|
|
|
Таким образом, точность близости будет О(h).
Если функция y(x) будет четырежды непрерывно дифференцируемой, то аналогичным образом с помощью формулы Тейлора можно установить оценку
│ |
y(x h) 2 y(x) y(x h) |
– |
y (x) │ с8h2. |
(5.25) |
|
h2 |
|||||
|
|
|
|
Однако при большей гладкости y(x) последняя оценка не может быть улучшена. Пусть коэффициенты a0(x), a1(x) уравнения (5.1) непрерывны на Ω = (a, b).
Тогда на множестве трижды непрерывно дифференцируемых функций в Ω с помощью оценок (5.22) и (5.24) получится неравенство
│Lhy – Ly │ c9h ,
которое выполнено для всех точек x, для которых x – h и x + h принадлежат отрезку [a, b], т. е. на отрезке [a+ h, b – h]. Следовательно, это неравенство справедливо для узлов xi сетки, принадлежащих Ωh.
93

Из последнего неравенства получится оценка (5.20) с порядком k = 1. Таким образом, точность близости операторов будет О(h). При этом в качестве нормы в пространстве Fh берётся равномерная норма
zh |
|
|
|
C ( h) |
max |
|
zi |
|
. |
|
|
|
zh |
|
|
||||||
|
|
Fh |
|
|
i 1,...,N 1 |
|
|
|
|
|
Пусть в дифференциальном уравнении (5.1) коэффициент a1(x) = 0 (тогда в разностном уравнении (5.10) отсутствует слагаемое  ), а коэффициент а0(х) есть непрерывная на (a, b) функция. Тогда на множестве четырежды непрерывно дифференцируемых функций в из неравенства (5.25) получается оценка (5.20) с порядком k = 2 в той же равномерной норме С( h). Следовательно, точность близости таких операторов L и Lh будет О(h2).
), а коэффициент а0(х) есть непрерывная на (a, b) функция. Тогда на множестве четырежды непрерывно дифференцируемых функций в из неравенства (5.25) получается оценка (5.20) с порядком k = 2 в той же равномерной норме С( h). Следовательно, точность близости таких операторов L и Lh будет О(h2).
Пусть в разностном уравнении (5.10) вместо разностного отношения 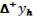 применено симметричное разностное отношение (5.8). Тогда при условии непрерывности функций a1(x) и а0(х) на множестве четырежды непрерывно дифференцируемых функций y(x) для такого оператора Lh будет выполнено неравенство (5.20) с k=2 в равномерной норме С( h). Это следует из оценок
применено симметричное разностное отношение (5.8). Тогда при условии непрерывности функций a1(x) и а0(х) на множестве четырежды непрерывно дифференцируемых функций y(x) для такого оператора Lh будет выполнено неравенство (5.20) с k=2 в равномерной норме С( h). Это следует из оценок
(5.23) и (5.25).
Неравенства (5.20) с соответствующим порядком k будут выполняться и в квадратичной норме L2( h ). Это следует из очевидного неравенства
║ ║L |
2 |
( |
h |
) |
║ ║C(Ωh). |
|
|
|
|
Перейдём к проверке условия устойчивости. Ограничимся более простой ситуацией, когда оператор Lh не содержит слагаемого a1,h yh .
Для доказательства нам потребуется скалярное произведение в L2( h ), опре-
деляемое равенством
N 1
(uh, vh)= U iVi h,
i 1
известное неравенство Коши – Буняковского
│(uh, vh)│ |
|
h |
|
|
|
v |
h |
u |
|
|
|||||
|
|||||||
|
|
|
|
|
|
|
|
с нормами в L2( h ). Кроме того, будет использована формула суммирования по частям
N 1 |
N |
|
(Ui+1 – Ui)Vi=UNVN – U1V0 – U i(Vi – Vi-1), |
i 1 |
i 1 |
|
94 |

имеющая некоторую аналогию с формулой интегрирования по частям в одномерном определённом интеграле.
Рассмотрим в L2(Ωh) скалярное произведение (Lhyh, yh), с указанным оператором Lh на множестве сеточных функций, удовлетворяющих граничному условию (5.11). Пусть при этом a0,h δ > 0.
Из формулы суммирования по частям при выполнении граничных условий (5.11) получим, что
N 1 |
|
|
|
|
|
|
|
|
|
|
|
N 1 |
( – 2yh, yh) = [ - ( yi)]yih= ( yi)] |i =1 y0 – ( yi) |i = N yN + [ yi )2h = |
||||||||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
i 1 |
N 1 |
|
|
|
|
|
|
|
|
|
|
|
|
= [ yi )2h 0. |
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N 1 |
|
|
|
|
|
|
N 1 |
|
(Lhyh, yh) = ( – |
2yh, yh) + a0,h(xi)yiyih δ |
yi2 h = δ || yh ||2L h (Ω h ). |
||||||||||
|
|
|
|
i 1 |
|
|
|
|
|
|
|
i 1 |
В силу граничных условий имеет место и неравенство |
|
|||||||||||
(L y |
, y |
) |
δ || y |
h |
||2 |
L 2 |
( |
Ω h |
) |
. |
(5.26) |
|
h |
h |
h |
|
|
|
|
|
|
||||
Неравенство означает, что Lh есть положительно определённый оператор как оператор, действующий из L 2 ( h ) в L 2 (Ω h ).
Из (5.26) и неравенства Коши – Буняковского получаем неравенство
|| Lhyh || L 2 (Ω h ) δ || yh ||L 2 ( Ω h ). (5.27)
Если yh есть решение уравнения (5.12), то из (5.27) имеем оценку
|
|
|
|
|
1 |
|| fh || L |
|
|
|
|
||
|| yh ||L |
2 |
( |
|
h |
) |
2 |
( Ω |
h |
), |
|||
|
||||||||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
которая и означает устойчивость.
Таким образом, если в уравнении (5.1) a1(x) = 0 (следовательно, в уравнении (5.10) a1,h = 0), то в случае трижды непрерывно дифференцируемого решения у(х) краевой задачи (5.1), (5.2) получим сходимость yh к y в норме L 2 ( h ) со скоро-
95
стью О(h), а в случае четырежды непрерывно дифференцируемого решения – со скоростью О(h2).
§ 6. Решение некоторых задач в EXCEL
Многие задачи, допускающие приближённое решение, можно решать в пакете EXCEL как по собственным схемам, так и при помощи надстройки «Поиск Решения». Здесь приведены некоторые стандартные алгоритмы.
Решение задач при помощи надстройки «Поиск Решения» 1. Решение уравнений
Дано уравнение f x 0 . Занесём в ячейку А1 любое число. В ячейку А2 запишем формулу для вычисления функции f x , где вместо x указываем А1.
Вызовем «Поиск Решения». Укажем, что ячейка А2 (с формулой) – целевая, и её значение надо привести к 0. Изменяемой ячейкой сделаем А1.
При необходимости укажем ограничения, если они подразумеваются по смыслу задачи. Например, если x 0 , указываем, что A1 ≥ 0. Выбираем команду «Выполнить». В ячейке А1 получим корень уравнения, а в А2 – число 0 (с предусмотренной точностью).
Если решение не получается (об этом выдаётся сообщение), можно поменять в пункте «Параметры» способ решения (метод Ньютона или метод сопряжённых градиентов) или поменять число в ячейке А1, чтобы начальное значение функции в А2 было не слишком велико.
2.Решение систем нелинейных уравнений
Вкачестве изменяемых ячеек выступает столбец, отведённый под n переменных, куда заносим произвольные числа. В других ячейках набираем необходимые формулы, соответствующие уравнениям системы. Предварительно каждое уравнение приводим к виду fi 0.
Вызвав «Поиск Решения», любую ячейку с формулой делаем целевой, указываем, что она должна обратиться в 0. Остальные уравнения должны выполняться
96
